Механічні коливання. Математичний маятник
РОЗДІЛ I
МЕХАНІЧНИЙ РУХ
УРОК № 9/9
Тема уроку. Механічні коливання. Математичний маятник
Тип уроку: засвоєння нових знань.
Мета уроку: ознайомити учнів із коливальним рухом; формувати вміння спостерігати та аналізувати фізичні явища; показати, як на практиці застосовуються знання про коливальний рух. обладнання: кулька на нитці; тягарець на пружині.
План уроку
Етапи | Час | Прийоми і методи |
I. Постановка навчальної проблеми | 5 хв. | Бесіда; |
II. Вивчення нового матеріалу | 20-25 хв. | Бесіда; демонстрація; записи на дошці та в зошитах |
III. Закріплення нового матеріалу | 10-15 хв. | Розв’язування задач; записи на дошці та в зошитах |
IV. Домашнє завдання | 1 хв. | Коментар учителя; записи на дошці та в щоденниках |
Хід уроку
I. Постановка навчальної проблеми
Бесіда
Сьогодні ми познайомимося ще з одним видом механічного руху – механічними коливаннями.
Демонстрація. Коливання кульки на нитці.
Питання класу: Яка особливість
Запис у зошит: Коливання – періодично повторювані рухи.
II. Вивчення нового матеріалу
Бесіда
Коливаються дерева під дією вітру, б’ється наше серце, коливається поплавець на поверхні води.
Завдання класу: Наведіть свої приклади коливального руху.
Під час коливання тіло періодично відхиляється від свого положення рівноваги.
Запис у зошит: Максимальне відхилення від положення рівноваги називають амплітудою коливань (А).
Питання класу: У яких одиницях СІ має вимірюватися амплітуда?
Всі коливання можна поділити на вільні та вимушені. У зошитах записуються означення вільних і вимушених коливань.
Завдання класу: Із наведених прикладів виберіть приклади вільних і вимушених коливань: рух пилки при розпилюванні дров; коливання іграшки неваляшки, рух гітарної струни; рух гілки під дією вітру, рух гойдалки на дитячому майданчику, рух голки у швейній машинці.
Коливання ще поділяються на затухаючі й незатухаючі. У зошитах записуються означення затухаючих і незатухаючих коливань.
Питання класу
– Чи можуть вільні коливання бути незатухаючими?
– Чи можуть вимушені коливання бути затухаючими?
Коливання, як уже було сказано,- це періодично повторюваний процес, отже, може характеризуватися періодом і частотою коливань.
Період (T) – час одного повного коливання:
[T] = с.
Частота (v) – кількість коливань за одиницю часу:
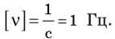
Зручніше за все вивчати коливальні рухи на прикладі маятників. Розрізняють пружинний і математичний маятники.
Демонстрація. Учитель демонструє зазначені вище маятники.
Більш докладно ми познайомимося з математичним маятником. Учні записують у зошитах означення математичного маятника.
Питання класу: Кульку на нитці можна вважати математичним маятником з певною натяжкою. Які характеристики математичного маятника (за означенням) не задовольняє кулька на нитці? (Кулька – не точкове тіло, а будь-яка реальна нитка – розтягується і має певну вагу.)
Голландський фізик і астроном Християн Гюйгенс (1629- 1695) у 1657 році винайшов маятниковий годинник. При цьому він детально вивчив коливальні рухи математичного маятника і встановив, що при малих амплітудах період коливань не залежить від амплітуди коливань, від маси маятника і цілком визначається довжиною нитки, на якій підвішано маятник.
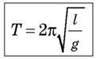
Як видно з формули, на період коливання математичного маятника впливає значення g – прискорення вільного падіння.
Значення g визначається не тільки формою і масою Землі, але й залежить від наявності у надрах планети важких (метали) або легких (газ, нафта) речовин. Таким чином, маятник може полегшувати роботу геологів при дослідженні покладів корисних копалин.
III. Закріплення нового матеріалу
Питання класу
– Що таке період і частота коливань? Як вони пов’язані між собою?
– Назвіть основну одиницю частоти. Що означає твердження: “Тіло коливається із частотою 3 Гц”?
– Чим вільні коливання відрізняються від вимушених? затухаючі від незатухаючих?
– Якими мають бути кулька і нитка, щоб маятник вважався математичним?
– Як зміниться період коливання маятника, якщо масу кульки зменшити у 2 рази? збільшити у 2 рази?
– Де на практиці використовують математичний маятник?
– Як зміниться період коливання математичного маятника, якщо його довжину збільшити у 4 рази?
– Що відбудеться, якщо нитку, на якій коливається маятник, скласти вдвічі?
Розв’язування задач
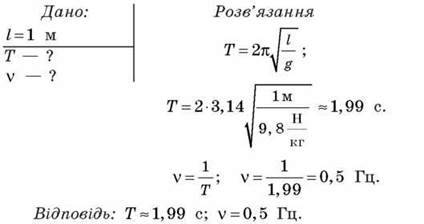
Задача 1. Визначте період і частоту коливань маятника, довжина якого 1 м.
Задача 2. Період коливань математичного маятника дорівнює 1 с. Визначте довжину маятника.
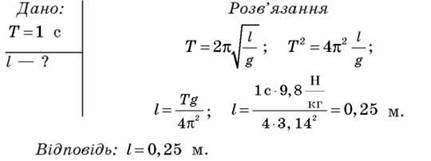
Задача 3. Порівняйте періоди коливань математичного маятника довжиною 1 м на Землі і на Місяці. Прискорення вільного падіння на Місяці вважати таким, що дорівнює 1,62 Н/кг.

Відповідь: різниця у періодах коливань становить 2,94 с.
IV. Домашнє завдання
[1]: § 6; впр. № 6 (задачі 3, 5, 6).
[2]: § 5.
[3]: СР – задачі 6.1-6.5;
ДР – задачі 6.11-6.13; 6.15;
ВР – задачі 6.17; 6.19; 6.20.
Творче завдання. Підготувати коротке повідомлення за однією із запропонованих тем: “Маятник – не тільки в годиннику!”, “Коливання у природі й техніці”, “Як використовують коливання”.
Підготуватися до лабораторної роботи № 3 за посібником [4]: домашняя работа № 3.
Скарбничка цікавих фактів
O А все-таки вона крутиться!
За одну секунду наша Земля повертається на 1/240 частку градуса. Щоб переконатися в цьому, французький учений Фуко провів дослід з величезним маятником (такий маятник був підвішений під куполом Ісаакієвського собору в Санкт-Петербурзі). Маятнику надають коливального руху і через якийсь час помічають, що площина його коливань повільно повертається. Земля, обертаючись, йде з-під маятника. якби кінець маятника викреслював траєкторію свого руху, то ми побачили б картину, зображену на рисунку.