Нестаціонарна дифузія
ФІЗИКА
Частина 2 МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА
Розділ 5 ЯВИЩА ПЕРЕНЕСЕННЯ
5.4. Нестаціонарна дифузія
У реальних умовах відбувається нестаціонарна дифузія. За нестаціонарних умов, коли маємо суміш з нерівномірним розподілом будь-якої компоненти, під час дифузії концентрації вирівнюються. Тому при нестаціонарній дифузії градієнт концентрації й самі концентрації компонент змінюються.
Нехай дві посудини з об’ємами V1 і V2 з’єднані між собою трубкою завдовжки l з площиною перерізу s (рис. 5.3) і наповнені сумішшю газів
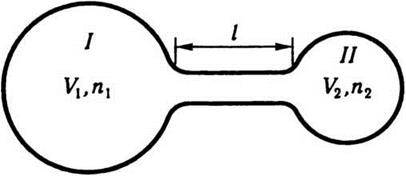
Рис. 5.3
Унаслідок дифузії концентрації в обох посудинах вирівнюватимуться, тобто різниця концентрацій Δn = n1 – n2 з часом зменшуватиметься.
Визначимо закон, за яким зменшується різниця концентрацій. Із закону Фіка випливає, що дифузійний потік
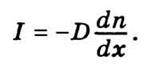
Припустімо, що концентрація заданої компоненти мала. Тоді можна записати, що
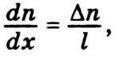
А рівняння (5.11) набере такого вигляду:
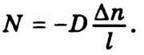
У процесі дифузії молекули дифундуючої компоненти переходитимуть із посудини І у посудину II. За нескінченно малий проміжок часу dt кількість молекул, які продифундують в посудину II, дорівнює
Оскільки молекули переходять із першої посудини в другу, їхня густина в посудині І зменшиться на деяку величину dn’, а в посудині II відповідно збільшиться на величину dn”. Можна ще записати так:
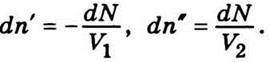
Тому концентрації n1 і n2 молекул у посудинах І і II через час dt стануть іншими:
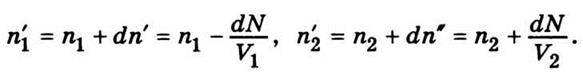
Визначимо різницю концентрацій через час dt:
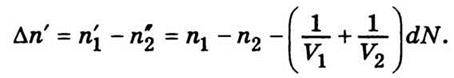
Підставимо сюди значення dN із (5.13), а різницю n1 – n2 позначимо через Δn, після чого дістанемо
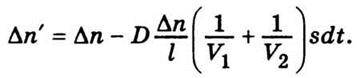
Звідси випливає, що зміна різниці концентрацій за час dt дорівнюватиме
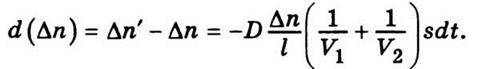
Величину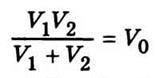 
називають зведеним об’ємом (при V1 = V2 = V зведений об’єм V0 = V/2 ).
Отже,
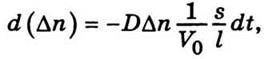
Або
Після інтегрування (5.14) дістанемо
Де А – стала інтегрування. Звідси
Стала А визначається з умови, коли відома початкова різниця концентрацій Δn0, тобто різниця концентрацій у момент часу t = 0. Підставимо ці значення часу в (5.16) і одержимо, що А = Δn0, тоді
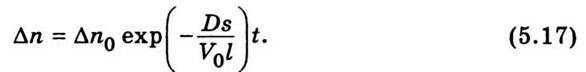
Ця рівність дає відповідь на поставлене питання про закон зменшення різниці концентрацій з часом. Різниця концентрацій з часом зменшується за експоненціальним законом і тим швидше, чим більше значення величини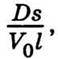 
яка для цього прикладу є сталою величиною. Величина, обернена цій сталій, 
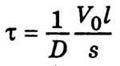має розмірність часу. Суть сталої τ полягає в тому, що вона дорівнює проміжку часу, який потрібен для того, щоб концентрація дифундуючої компоненти зменшилась у е разів. Величину τ називають сталою часу процесу.
Рівняння (5.17) можна записати так:
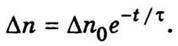
Отже, чим менша стала часу, тим швидше відбувається процес вирівнювання.
Дифузія в газах при атмосферному тиску – процес повільний.
Наприклад, для суміші азоту і кисню різниця концентрацій зменшиться утричі лише за 5 год.
(1 votes, average: 5.00 out of 5)
Loading...