Головна ⇒ 📌Математика ⇒ Обернена пропорційна залежність

Обернена пропорційна залежність

Розділ 3 Відношення і пропорції

§26. Обернена пропорційна залежність

Нехай площа прямокутника дорівнює 36 см2, а довжина і ширина прямокутника є натуральними числами. Деякі з можливих значень довжини а і ширини b подано у таблиці.

А, см	36	18	12	9	6
B, см	1	2	3	4	6

Кожного разу маємо різні значення довжини і ширини прямокутника, проте добуток цих значень є сталим числом. Воно дорівнює

площі прямокутника (у см2), тобто числу 36:

36 ∙ 1 = 18 ∙ 2 = 12 ∙ 3 = 9 ∙ 4 = 6 ∙ 6 = 36.

– Дві величини, добуток відповідних значень яких є сталим, називають обернено пропорційними.

Зауважимо, що з відповідних значень однієї з двох обернено пропорційних величин і значення, оберненого до другої величини, можна скласти пропорцію. Дійсно, виходячи, наприклад, з умови 12 ∙ 3 = 9 ∙ 4, можна скласти пропорцію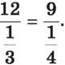

Цим і пояснюється назва обернено про порційних величин.

Обернено пропорційними величинами є довжина і ширина прямокутника при сталій площі прямокутника; швидкість тіла і час при сталому

шляху; кількість робітників і час виконання роботи, якщо обсяг роботи є сталим тощо.

Розглянемо два значення довжини прямокутника a = 18 см і a = 9 см та відповідні їм значення ширини b = 2 см і b = 4 см. Удвічі більшому значенню довжини прямокутника відповідає вдвічі менше значення його ширини. Можна зробити висновок про те, що обернено пропорційні величини мають таку властивість:

Звідси 6х = 10 ∙ 12; 6х = 120; x = 20 (год).

Відповідь. 20 год.

Не будь-які дві величини є прямо пропорційними чи обернено пропорційними. Наприклад, маса дитини збільшується при збільшенні її віку. Але ці величини не є пропорційними, оскільки при збільшенні удвічі віку дитини її маса удвічі не збільшується.

Із збільшенням (зменшенням) значення однієї з обернено пропорційних величин у кілька разів значення другої величини зменшується (збільшується) в таку саму кількість разів.

Звідси можна зробити висновок, що якщо величини обернено пропорційні, то відношення значень однієї величини дорівнює оберненому відношенню відповідних значень іншої величини.

Дійсно, у розглянутому вище прикладі відношення значень a = 18 см і a = 9 см дорівнює оберненому відношенню відповідних значень b = 2 см іb = 4 см: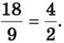

Отже, задачі, пов’язані з оберненою пропорційною залежністю, як і задачі, пов’язані із прямою пропорційною залежністю, можна розв’язувати за допомогою пропорції.

Задача. 10 робітників виконують певну роботу за 12 годин. Скільки часу знадобиться для виконання такої роботи шести робітникам, якщо продуктивність праці всіх робітників однакова?

Розв’язання. Число робітників і час виконання даної роботи є величинами обернено пропорційними (при однаковій продуктивності праці всіх робітників).

Нехай 6 робітників виконують роботу за x год. Запишемо умову задачі схематично:

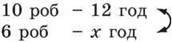
Двонапрямлена стрілка праворуч означає, що величини у задачі обернено (а не прямо) пропорційні, і “підказує”, що при складанні відповідного рівняння 12 і x треба поміняти місцями. Отже, маємо рівняння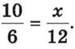

Які величини називають обернено пропорційними? Наведи приклади обернено пропорційних величин. Яку властивість мають обернено пропорційні величини?

672. (Усно) Значення однієї з двох обернено пропорційних величин зменшилося в 6 разів. Як змінилося значення другої величини?

673. Значення однієї з двох обернено пропорційних величин збільшилося в 10 разів. Як змінилося значення другої величини?

674. (Усно) Учень мав деяку суму коштів і витратив усю на 6 однакових зошитів. Скільки зошитів на ці гроші зміг би купити учень, якби ціна зошита була:

1) удвічі меншою; 2) удвічі більшою?

675. (Усно) Визнач, які з величин є прямо пропорційними, які – обернено пропорційними, а також величини, які не є прямо пропорційними чи обернено пропорційними:

1) кількість одноманітного краму та його вартість;

2) ціна краму та його вартість;

3) ціна краму та його кількість при сталій вартості;

4) продуктивність праці робітників та тривалість роботи при сталій кількості роботи;

5) кількість робітників та кількість виконаної роботи при сталій продуктивності;

6) вік дитини та її зріст.

676. Визнач, які з величин є прямо пропорційними, а які – обернено пропорційними:

1) швидкість рівномірного руху та його тривалість при сталій довжині шляху;

2) швидкість руху та довжина пройденого шляху;

3) чисельник та значення дробу при сталому знаменнику;

4) знаменник та значення дробу при сталому чисельнику.

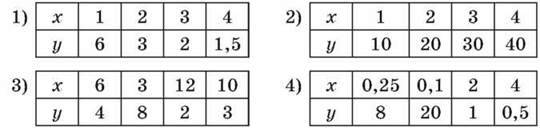
677. (Усно) Визнач, в яких таблицях величини x і у є обернено пропорційними.

678. Якщо вантажівка перевозитиме за годину по 4 т зерна, то все зерно зможе перевезти за 10 год. Проте вантажівка за годину перевозила по 5 т зерна. За скільки годин було перевезено все зерно?

679. Два прямокутники мають однакову площу. Довжина одного прямокутника 8 см, а ширина 3 см. Знайдіть довжину другого прямокутника, якщо його ширина дорівнює 4 см.

680. Пішохід пройшов відстань між двома селами за 1,5 год зі швидкістю 3,6 км/год, а на зворотний шлях витратив 2,4 год. З якою швидкістю він повертався?

681. Є два сувої тканини однакової вартості. У першому сувої 60 м тканини за ціною 64,8 грн за 1 м. Скільки коштує 1 м тканини у другому сувої, якщо в ньому 40 м тканини?

682. Два шківи з’єднано приводним пасом (мал. 14). Довжина ободу першого шківа 21 см, а другого – 14 см.

Скільки обертів за хвилину робить перший шків, якщо другий обертається 600 разів за хвилину?

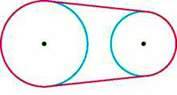
Мал. 14

A	0,4	25	0,04	0,25	0,01
B	0,2	20	4	10

684. Літак за кожні 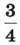години пролітає 270 км, а всю від стань між містами долає за 4,5 години. Назад літак повертається зі швидкістю 405 км/год. За скільки годин літак долає зворотний шлях?

683. Заповни в зошиті таку таблицю, якщо величини a і b є обернено пропорційними.

685. Велосипедист за кожні 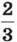години проїжджає 12 км, а всю відстань між селами проїхав за 3,5 год. Повертався велосипедист зі швидкістю 15 км/год. Скільки годин велосипедист повертався назад?

686. Для перевезення деякого вантажу 3 машини вантажопідйомністю 7,5 т здійснили по 8 рейсів. Скільки треба машин вантажопідйомністю 4,5 т, щоб на перевезення вантажу знадобилося 10 рейсів?

687. Наявного запасу пального вистачить на 10 днів для 9 тракторів при роботі по 7 годин на день. На скільки днів вистачить цього запасу пального для 14 таких тракторів, якщо вони працюватимуть по 9 годин на день?

688. Запиши звичайні дроби у вигляді десяткових, а потім у вигляді відсотків:

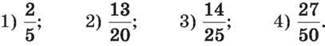
689. Оператор комп’ютерного набору планував за день набрати 20 сторінок тексту, але перевиконав план на 15 %. Скільки сторінок набрав оператор за день?

690. Поясни, чому число 1,6(36n -1) є натуральним при будь-якому натуральному значенні n.