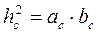Ознаки подібності прямокутних трикутників. Пропорційні відрізки в прямокутному трикутнику
Урок № 32
Тема. Ознаки подібності прямокутних трикутників. Пропорційні відрізки в прямокутному трикутнику
Мета: сформулювати ознаку подібності прямокутних трикутників за гострим кутом, на основі якої довести метричні співвідношення в прямокутному трикутнику. Домогтися засвоєння учнями змісту ознаки подібності прямокутних трикутників і метричних співвідношень у прямокутному трикутнику га їх доведення.
Сформувати первинні вміння відтворювати вивчені твердження, записувати метричні співвідношення між відрізками прямокутного
Тип уроку: засвоєння вмінь та навичок.
Наочність та обладнання: конспект “Подібність прямокутних трикутників”.
Хід уроку
I. Організаційний етап
II. Перевірка домашнього завдання
Правильність виконання задач домашньої роботи перевіряється під час усної фронтальної роботи за рисунками до задач, виконаними на дошці заздалегідь.
ІІІ. Формулювання мети і завдань уроку
Вчитель нагадує учням про те, що в геометрії виділяють
Серед усіх видів трикутників (за кутами) виділяються трикутники, про які можна сказати, що:
– один з кутів завжди дорівнює сумі двох інших;
– вони не можуть бути рівносторонніми, але можуть бути рівнобедреними;
– для того щоб визначити решту кутів цього трикутника, достатньо знати тільки один з його менших кутів.
(Зрозуміло, що мова йде про прямокутні трикутники.)
Отже, мета уроку – формулювання ознаки подібності прямокутних трикутника та дослідження сфери її практичного застосування.
IV. Актуалізація опорних знань
З метою успішного засвоєння учнями ознаки подібності прямокутних трикутників, метричних співвідношень у прямокутному трикутнику, а також їх доведення, учням слід активізувати такі знання і вміння: ознака подібності трикутників за двома кутами; означення прямокутного трикутника та властивості гострих кутів прямокутного трикутника; застосування поняття про перпендикуляр до прямої, похила та проекція похилої на дану пряму; основні властивості пропорції.
Виконання усних вправ
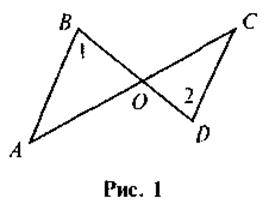
1. Доведіть, що? АВО ~ ?DCO, якщо 
1 = 2 (рис. 1).
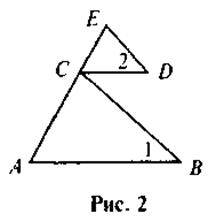
2. Доведіть, що? АВС ~ ?CDE, якщо AB || CD, 1 = 2 (рис. 2).
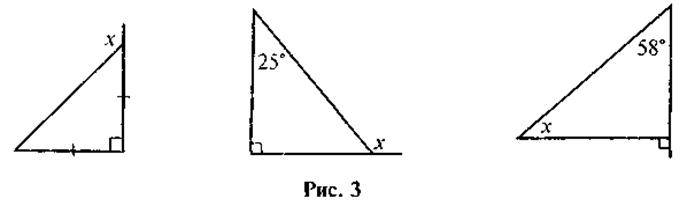
3. У кожному з наведених випадків обчисліть міру кута х (рис. 3).
4. Зробіть рисунок, на якому один і той самий відрізок був би одночасно і перпендикуляром, і похилою.
5. Якщо 7а = 9b, то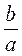 
= ?
V. Засвоєння знань
План вивчення нового матеріалу
1. Ознака подібності прямокутних трикутників (за гострим кутом).
2. Уявлення про зміст поняття середнє пропорційне число між двома числами.
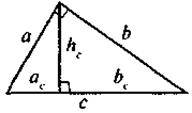
3. Теорема (метричні співвідношення в прямокутному трикутнику): формулювання і доведення.
@ Ознаки подібності прямокутних трикутників, а також метричні співвідношення в прямокутному трикутнику, що безпосередньо випливають з ознаки подібності прямокутних трикутників за гострим кутом, традиційно вивчаються в темі “Подібність трикутників” (у деяких посібниках метричні співвідношення називають середні пропорційні відрізки в прямокутному трикутнику). Зміст відповідного параграфа нового підручника майже повністю повторює зміст відповідних розділів традиційного підручника геометрії. Тому вивчення матеріалу уроку проводиться за традиційною схемою.
Схема
Доведення ознак подібності прямокутних трикутників за гострим кутом |
|
Доведення подібності будь-якого прямокутного трикутника та прямокутних трикутників, цю утворюються, якщо в даному трикутнику провести висоту до гіпотенузи |
|
Запис рівностей відношень відповідних сторін них подібних прямокутних трикутників v вигляді пропорції |
|
Використання здобутих пропорцій, основної властивості пропорції |
Деякі зміни, які внесені авторами нового підручника до змісту матеріалу щодо подібності прямокутних трикутників, є додатковою інформацією.
Так, додатково автори підручника пропонують вивчити:
Ознаки подібності прямокутних трикутників за двома катетами та за гіпотенузою і катетом.
1. Сформулюйте і доведіть ознаку подібності прямокутних трикутників за двома катетами.
2. Сформулюйте і доведіть ознаку подібності прямокутних трикутників за гіпотенузою і катетом.
Зміст поняття про середнє пропорційне число між двома даними числами (для кращого розуміння учнями змісту теореми, а тому для кращого запам’ятовування формулювання теореми).
А самі метричні співвідношення в прямокутному трикутнику автори підручника записали у вигляді теореми (раніше ці співвідношення розглядали як деякі співвідношення в прямокутному трикутнику). Зміна статусу цих тверджень, без зміни їх змісту, має суто психологічне значення – знання формулювання теореми та вміння її застосовувати є обов’язковою програмовою вимогою.
До матеріалу, поданого в підручнику, автор посібника пропонує додати один із корисних наслідків з метричних співвідношень, а саме: якщо а, b – катети прямокутного трикутника, с – його гіпотенуза, a hc – висота, що проведена до гіпотенузи, то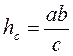 
. (Доведення с цього наслідку можна провести як розв’язання відповідної додаткової задачі.)
Оскільки навчальний матеріал не є складним, то пропонуємо учням самостійну роботу з його вивчення (за підручником).
Конспект 12 | ||
Подібність прямокутних трикутників | ||
Ознаки | ||
|
|
|
Метричні співвідношення | ||
А2 = с – ас, B2 = c – bc,
Наслідки з метричних співвідношень: |
| |
1) | 2) |
V. Формування первинних умінь
Розуміння ознаки подібності прямокутних трикутників за гострим кутом досягається під час виконання завдання. Чи подібні два прямокутні трикутники, якщо:
А) вони мають спільний кут;
Б) вони мають спільний гострий кут;
В) один із них має кут 20°, а інший – кут 70°;
Г) один із них має кут 50°, а катет другого удвічі менший від гіпотенузи?
Формування первинних умінь застосовувати вивчену ознаку відбувається на етапі розв’язування учнями вправ.
Виконання усних вправ
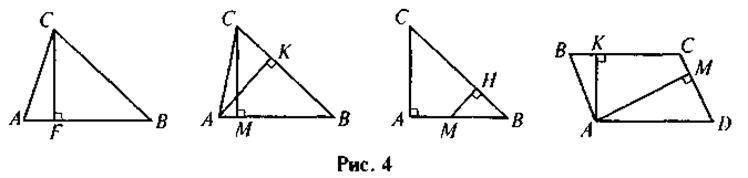
1. На рис. 4 знайдіть пари подібних трикутників. Свої міркування обгрунтуйте. Запишіть пропорційність відповідних сторін.
2. На рисунку 5 знайдіть подібні трикутники і доведіть їх подібність.
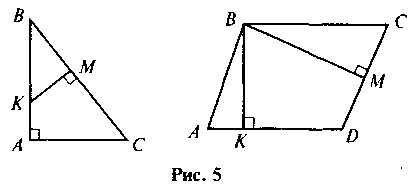
На застосування подібності прямокутних трикутників учні розв’язують письмові вправи.
Виконання письмових вправ
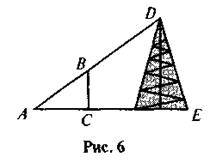
Спостерігач, що знаходиться в точці А, бачить кінець жердини В і верхню точку вежі D, причому точки А, В і D розміщені на одній прямій (рис. 6). Визначте висоту вежі, якщо ВС= 4 м, АС = 6 м, АЕ = 90 м.
VI. Формування навичок та вмінь
Формуванню вмінь записувати та використовувати метричні співвідношення сприятиме виконання усних вправ.
Виконання усних вправ
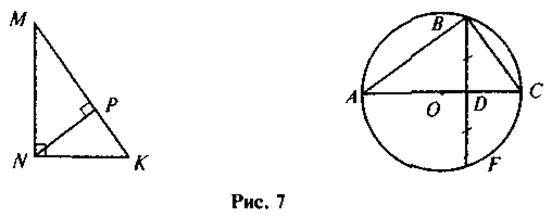
Запишіть метричні співвідношення для зображених на рис. 7 прямокутних трикутників:
Виконання письмових вправ
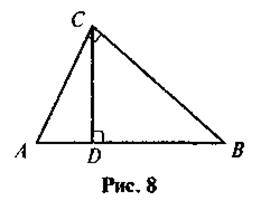
1. У прямокутному трикутнику ABC (C = 90°) проведено висоту CD (рис. 8). Знайдіть:
А) CD, якщо AD = 4 см, DB = 25 см;
Б) АС і ВС, якщо АВ = 50 см, AD = 18см.
2. Доведіть, що проекції катетів на гіпотенузу прямокутного трикутника відносяться як квадрати катетів: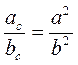 
.
@ Під час доведення подібності трикутників вимагаємо від учнів виконання міркувань за вивченою на попередніх уроках схемою з поправкою на зміст ознаки. (Розглянемо трикутники… і… У них кути… і… – прямі, кути… і… – рівні, отже, трикутники… і… подібні за гострим кутом).
Розв’язуючи задачі на застосування метричних співвідношень у прямокутному трикутнику, слід вимагати від учнів спочатку відтворення словесного формулювання, а вже потім – виконання відповідних їм символічних записів.
VII. Підсумки уроку
Чи правильні записи зроблені відповідно до рис. 9? Якщо ні, виправте помилку.
1) АМ + ВМ = АВ;
2) ВС2 = МВ – МА;
3) CM = AM – MB;
4) 
;
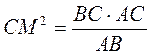5) АС2 = АМ – АВ.
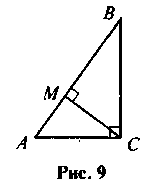
VIII. Домашнє завдання
Вивчити зміст та доведення ознак подібності прямокутних трикутників.
Розв’язати задачі.
1. Для побудови четвертого пропорційного відрізка х =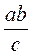 
учень запропонував побудувати прямокутний трикутник із катетами а і b та гіпотенузою с і провести в ньому висоту hc, яка буде дорівнювати х. Другий учень стверджує, що цей спосіб хибний. Хто з учнів правий?
2. На рисунку 10 знайдіть подібні трикутники і доведіть їх подібність.
3. Висота дерева дорівнює 9,2 м, а довжина тіні людини, зріст якої 1,8 м, дорівнює 2,7 м. Знайдіть довжину тіні дерева.
4. Знайдіть периметр прямокутного трикутника, висота якого ділить гіпотенузу на відрізки завдовжки 4,5 см і 8 см.
(1 votes, average: 5.00 out of 5)
Loading...