Період власних коливань у коливальному контурі
2-й семестр
ЕЛЕКТРОДИНАМІКА
4. Електромагнітні коливання й хвилі
УРОК 3/45
Тема. Період власних коливань у коливальному контурі
Мета уроку: навчити учнів визначати період і частоту власних коливань у коливальному контурі.
Тип уроку: урок вивчення нового матеріалу.
ПЛАН УРОКУ
Контроль знань | 3 хв. | 1. Вільні електромагнітні коливання в коливальному контурі. 2. Перетворення енергії в коливальному контурі. |
Демонстрації | 3 хв. | Залежність |
Вивчення нового матеріалу | 25 хв. | 1. Формула Томсона. 2. Формула Томсона як наслідок закону збереження енергії. 3. Період коливань у реальному коливальному контурі. |
Закріплення вивченого матеріалу | 14 хв. | 1. Якісні питання. 2. Навчаємося розв’язувати задачі. |
ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ
1. Формула Томсона
Формула коливань пружинного маятника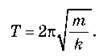 
Аналогом маси m для коливань у контурі є індуктивність L. А щоб
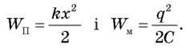Оскільки сила струму 
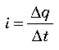є аналогом швидкості 
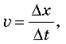заряд q можна вважати аналогом зміщення у вантажу (деформації пружини) х. Тоді, зіставивши формули енергії, можна зробити висновок про аналогії між величинами k й 1/C.Отже, замінивши m на L, а k на 1/C, одержуємо формулу періоду вільних електромагнітних коливань у коливальному контурі:
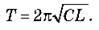
Ця формула називається формулою Томсона.
З формули Томсона випливає, що, змінюючи L і C, можна одержувати електричні коливання заданої частоти:
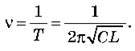
2. Формула Томсона як наслідок закону збереження енергії
За визначенням сила струму дорівнює швидкості зміни заряду: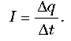 
У будь-який момент часу сила струму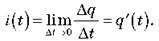 
Відповідно, швидкість зміни сили струму: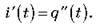 
Повна енергія ідеального коливального контуру не змінюється з часом: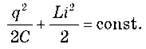 
Знайдемо похідні від правої й лівої частини цієї рівності: 
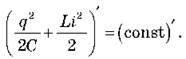Звідси одержуємо:
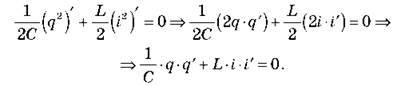
З огляду на те, що i = q’, а i’= q”, маємо:
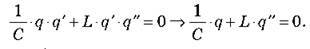
Звідси: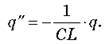 
Це рівняння є диференціальним рівнянням другого порядку, розв’язанням якого буде функція косинуса (синуса).
Якщо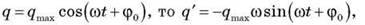 
А 
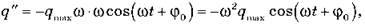у такий спосіб
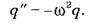
Отже, заряд на обкладках конденсатора ідеального коливального контуру змінюється за гармонічним законом:
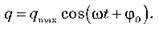
З виразів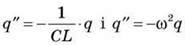 
маємо:
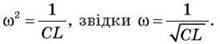
Оскільки період коливань T = 2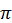
/?, то одержуємо формулу Томсона: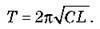 
Сила струму пов’язана із зарядом на обкладках конденсатора співвідношенням:
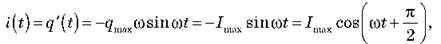
Де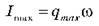 
– амплітудне значення сили струму.
Коливання сили струму в контурі випереджають коливання заряду на обкладках конденсатора за фазою на 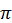/2.
3. Період коливань у реальному коливальному контурі
У реальному коливальному контурі завжди є певні втрати енергії. Всі ці втрати умовно вважають втратами на активному опорі R. Наявність активного опору призводить до того, що амплітуда сили струму поступово зменшується й коливання припиняються. Таким чином, вільні електромагнітні коливання в реальному контурі є загасаючими.
Для загасаючих коливань формула Томсона має такий вигляд:
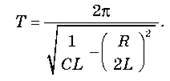
ПИТАННЯ ДО УЧНІВ У ХОДІ ВИКЛАДУ НОВОГО МАТЕРІАЛУ
Перший рівень
1. Яка роль індуктивності і ємності в коливальному контурі?
2. Чому електромагнітні коливання в реальному контурі завжди є загасаючими?
3. Як зміниться період вільних коливань у коливальному контурі, якщо збільшити відстань між пластинами конденсатора?
4. Як зміниться частота вільних коливань у коливальному контурі, якщо в котушку внести залізний сердечник?
Другий рівень
1. Увімкнений у коливальний контур конденсатор заповнений діелектриком проникністю? = 4. Як зміниться частота власних коливань контуру?
2. У коливальному контурі відбуваються вільні незатухаючі коливання частотою 50 кГц. З якою частотою змінюється енергія електричного поля конденсатора?
ЗАКРІПЛЕННЯ ВИВЧЕНОГО МАТЕРІАЛУ
1). Якісні питання
1. Ємність конденсатора коливального контуру зменшили у 2 рази. У скільки разів треба змінити індуктивність котушки, щоб частота коливань у контурі залишилася попередньою?
2. Пластини плоского конденсатора, увімкненого в коливальний контур, спочатку зближають, а потім відсувають одну від одної. Як при цьому змінюється частота електричних коливань?
2). Навчаємося розв’язувати задачі
1. Максимальна напруга на обкладках конденсатора ідеального коливального контуру досягає 1 кВ. Визначте період коливань у контурі, якщо за амплітудного значенні сили струму 1 А, енергія магнітного поля в контурі становить 1 мДж.
Розв’язання. Для визначення періоду коливань скористаємося формулою Томсона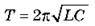 
й законом збереження енергії
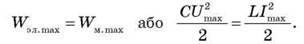Перемноживши ці рівності, одержуємо: 
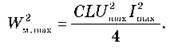Звідси: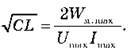 
Остаточно маємо: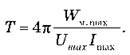 
Перевіривши одиниці величин і підставивши числові значення, визначаємо період коливань: 13 мкс.
2. Частота коливань у коливальному контурі дорівнює 100 кГц. Якою стане частота коливань, якщо зменшити ємність конденсатора у 8 разів, а індуктивність котушки збільшити у 2 рази?
3. Яка частота вільних електромагнітних коливань у контурі, що складається з конденсатора ємністю 250 пФ і котушки індуктивністю 40 мкГн?
4. Заряд на пластині конденсатора коливального контуру зменшився від амплітудного значення до половини цього значення. Через яку частину періоду коливань цей заряд матиме такий самий модуль, але протилежний знак?
Відповідь: через 1/6 періоду.
ЩО МИ ДІЗНАЛИСЯ НА УРОЦІ
– Формула Томсона:
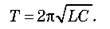
– Частота електромагнітних коливань:
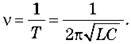
– Формула Томсона для загасаючих коливань:
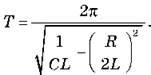
Домашнє завдання
1. Підр-1: § 28; підр-2: § 15 (п. 3).
2. Зб.:
Рів1 № 11.9; 11.10; 11.11; 11.12.
Рів2 № 11.24; 11.25; 11.26; 11.27.
Рів3 № 11.32, 11.33; 11.44; 11.45.
(3 votes, average: 2.33 out of 5)
Loading...