Побудова графіків функцій за допомогою геометричних перетворень відомих графіків функцій
УРОК 3
Тема. Побудова графіків функцій за допомогою геометричних перетворень відомих графіків функцій
Мета уроку: Формування умінь будувати графіки функцій за допомогою восьми базових перетворень графіка функції
У = f(x): у = – f(x); у = f(-x); у = f(x) + b; у = f(x + a); у = af(x); у = f(ax); у = f(¦x¦); у = ¦f(x)¦.
І. Перевірка домашнього завдання.
1. Розв’язування вправ, аналогічних до домашніх.
1) Знайдіть область визначення функції: а) 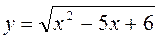 ; б)
; б) 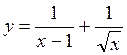 .
.
А) Через те що арифметичний квадратний корінь існує лише
 0 . Розв’яжемо нерівність методом інтервалів (знайдемо нулі функції g = х2 – 5х + 6, нанесемо їх на координатну пряму і визначимо знак функції на кожному проміжку) (рис. 15).
0 . Розв’яжемо нерівність методом інтервалів (знайдемо нулі функції g = х2 – 5х + 6, нанесемо їх на координатну пряму і визначимо знак функції на кожному проміжку) (рис. 15).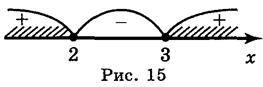
Отже, D(y) = (- ; 2]
; 2]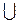 [3; +
[3; + ).
).
Б) D(y) знаходимо розв’язавши систему 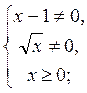
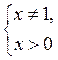 . Отже, D(y) = (0; 1)
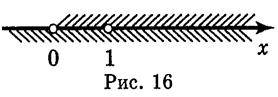
. Отже, D(y) = (0; 1)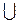 (1; +
(1; + ) (рис. 16).
) (рис. 16).
2) Дослідіть на парність і непарність функцію: а) f(x) = х2(2x – х3) ; б)
А) Через те що D(f) = R і f(-x) = (-х)(2(-х) – (-х)3) = х2(-2х + х3) = – x2(2x – х3) = – f(x), f(x) = x2(2x – х3) – непарна.
Б) Через те що D(f) = R і 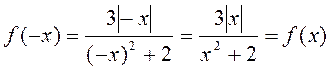 , то
, то 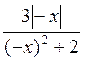 – парна.
– парна.
II. Повторення і систематизація знань учнів про геометричні перетворення графіків.
Запас функцій, графіки яких ви вмієте будувати, поки невеликий. Але використовуючи відомі із курсів геометрії і алгебри відомості про перетворення фігур, цей список можна суттєво розширити. Згадаємо елементарні перетворення графіка функції у = f(x) за допомогою таблиці 2.
Таблиця 2
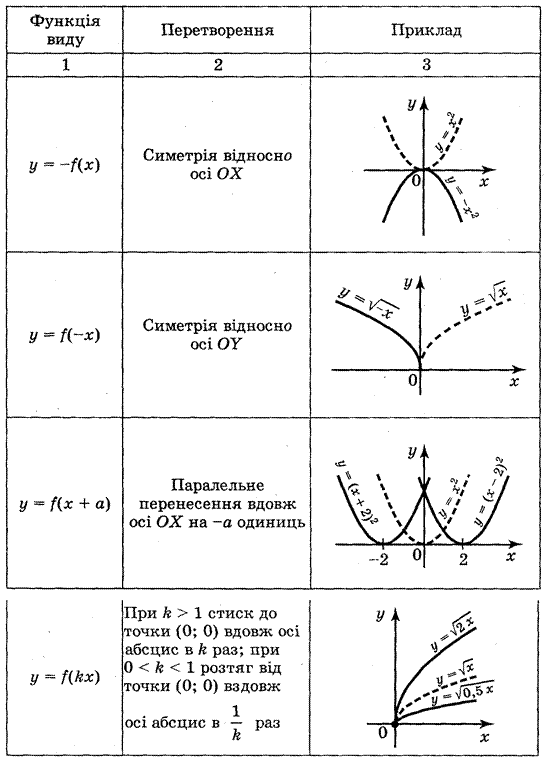
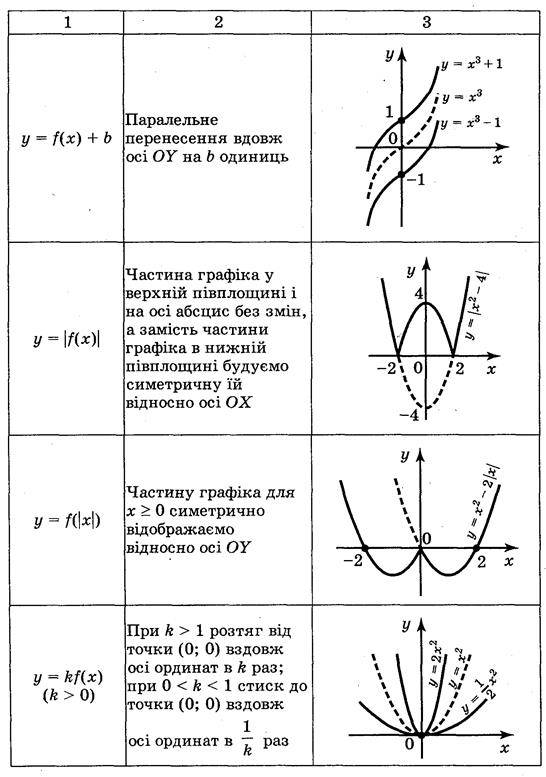
III. Формування умінь будувати графіки за допомогою геометричних перетворень відомих графіків
Колективне виконання вправ № 3 (1; 2; 3; 14; 19).
IV. Підсумок уроку
V. Домашнє завдання
Розділ І § 1 (3). Запитання і завдання для повторення № 27-31. Вправа № 3 (7, 8, 9, 4, 5, 6, 18).
Related posts:
- Побудова графіків тригонометричних функцій УРОК 9 Тема. Побудова графіків тригонометричних функцій Мета уроку: побудова графіків функцій у = sin х, у = cos x, у = tg х, у = ctg x. Формування умінь будувати графіки функцій: у = Asin (kx + b), у = Acos (kx + b), у = Atg (kx + b), у = Actg (kx […]...
- Найпростіші перетворення графіків функцій УРОК № 21 Тема. Найпростіші перетворення графіків функцій Мета уроку: закріпити знання учнів про види геометричних перетворень графіків функцій і зв’язок між видом перетворення та видом рівняння, що задає дану функцію. Закріпити схеми міркувань, що передують побудові графіка деякої функції шляхом геометричних перетворень графіка однієї з елементарних функцій. Закріпити вміння виконувати послідовні перетворення графіків елементарних […]...
- Перетворення графіків функцій – Функції та графіки Математика – Алгебра Функції та графіки Перетворення графіків функцій 1. Графіки функцій і є симетричними відносно осі Ox. 2. Щоб побудувати графік функції , треба графік функції розтягнути від осі Ox в k разів, якщо , або стиснути його в k разів до осі Ox, якщо . 3. Щоб побудувати графік функції , треба графік […]...
- Приклади функцій і їх графіків Математика – Алгебра Функції Приклади функцій і їх графіків Лінійна функція Лінійною називається функція, яку можна задати формулою , де х – аргумент, а k і b – дані числа. Графік лінійної функції – пряма. k називається Кутовим коефіцієнтом прямої, яка є графіком лінійної функції. Кожна пряма на координатній площині, яка не є перпендикулярною до […]...
- Розв’язування вправ. Самостійна робота УРОК 4 Тема. Розв’язування вправ. Самостійна робота Мета уроку: формування умінь будувати графіки функцій за допомогою геометричних перетворень. І. Перевірка домашнього завдання 1. Один учень відтворює розв’язування вправи № 3 (4; 5; 6), другий – № 3 (7; 8; 9), третій – № 3 (18). 2. Математичний диктант. Запишіть формулою функцію, графік якої одержано в […]...
- Практична робота 4. Ділова графіка. Побудова діаграм і графіків на основі табличної інформації. Друкування діаграм ТЕМА 5.4. ЕЛЕКТРОННІ ТАБЛИЦІ (10 ГОДИН) Урок 55 Практична робота 4. Ділова графіка. Побудова діаграм і графіків на основі табличної інформації. Друкування діаграм Мета: – навчити учнів будувати діаграми та графіки за допомогою засобів ЕТ; – розвивати вміння самостійно міркувати, аналізувати та використовувати інформацію; – виховувати сучасну людину, яка спирається на естетичні цінності при оформленні […]...
- Графіки тригонометричних функцій Математика – Алгебра Тригонометричні функції Графіки тригонометричних функцій Для побудування графіків тригонометричних функцій візьмемо . Побудуємо графік функції (див. рисунок). Ця крива називається синусоїдою. Графік функції можна дістати з графіка функції паралельним перенесенням його вліво вздовж осі Ox на одиниць. Це випливає з формули . Побудуємо графік функції : Зверніть увагу: значення , , не […]...
- Періодичність тригонометричних функцій Математика – Алгебра Тригонометричні функції Періодичність тригонометричних функцій Функція називається Періодичною з періодом , якщо для будь-якого x з області визначення функції числа і також належать області визначення й виконується умова: . Якщо T – період функції , то всі числа виду nT, де , , також є періодами функції. Щоб побудувати графік періодичної функції […]...
- Огляд властивостей основних функцій УРОК 2 Тема. Огляд властивостей основних функцій Мета уроку: Повторення і узагальнення властивостей елементарних функцій: у = kx + b, у = , у = х2, у= х3, у = , у = , у = ?х2 + bx + с. І. Перевірка домашнього завдання 1. Один учень пояснює розв’язання вправи № 1 (5), другий […]...
- Формули суми (різниці) однойменних тригонометричних функцій. Перетворення добутку тригонометричних функцій у суму УРОК 15 Тема. Формули суми (різниці) однойменних тригонометричних функцій. Перетворення добутку тригонометричних функцій у суму Мета уроку: вивчення формул суми і різниці однойменних тригонометричних функцій і формул перетворення добутку тригонометричних функцій у суму. Формування умінь учнів застосовувати вивчені формули для спрощення виразів та обчислень. Обладнання. Таблиця “Формули перетворення суми в добуток (добутку в суму)”. І. […]...
- Розв’язування вправ на застосування перетворень виразів Урок № 56 Тема. Розв’язування вправ на застосування перетворень виразів Мета: узагальнити та систематизувати знання та вміння учнів щодо різних видів перетворень цілих виразів; відпрацювати навички застосування набутих знань та вмінь під час розв’язування завдань на доведення подільності. Тип уроку: узагальнення та систематизація знань. Хід уроку I. Організаційний момент Перевіряємо готовність учнів до уроку, повідомляємо […]...
- Періодичність тригонометричних функцій УРОК 8 Тема. Періодичність тригонометричних функцій Мета уроку: Введення поняття періодичної функції; знаходження найменших додатних періодів тригонометричних функцій; формування умінь знаходити періоди функцій У = sin (kx + b), у = cos (kx + b), У = tg (kx + b), у = ctg (kx + b). І. Перевірка домашнього завдання 1. Побудуйте на одиничному […]...
- Читання чотирицифрових чисел. Розкладання чисел на розрядні доданки. Утворення чотирицифрових чисел із розрядних чисел. Кути, види кутів, побудова кутів за допомогою лінійки (№№ 176-184) Тема. Читання чотирицифрових чисел. Розкладання чисел на розрядні доданки. Утворення чотирицифрових чисел із розрядних чисел. Кути, види кутів, побудова кутів за допомогою лінійки (№№ 176-184). Мета. Формувати в учнів уміння читати чотирицифрові числа в межах 10000, розкладати їх на розрядні доданки, утворювати числа з розрядних доданків; розширити поняття про куги, вчити будувати різні кути за […]...
- Практична робота 3. Використання формул і вбудованих функцій у середовищі табличного процесора. Використання логічних функцій для опрацювання табличної інформації ТЕМА 5.4. ЕЛЕКТРОННІ ТАБЛИЦІ (10 ГОДИН) Урок 54 Практична робота 3. Використання формул і вбудованих функцій у середовищі табличного процесора. Використання логічних функцій для опрацювання табличної інформації Мета: – формувати теоретичну базу знань учнів з теми, спираючись на міжпредметні зв’язки; – розвивати практичні вміння та навички щодо опрацювання табличної інформації за допомогою формул та вбудованих […]...
- Метод геометричних місць Урок № 48 Тема. Метод геометричних місць Мета: домогтися засвоєння учнями схеми дій, що покладено в основу методу геометричних місць. Сформувати вміння: – відтворювати схему, що лежить в основі методу геометричних місць; – виконувати дії, що передбачені цією схемою. Тип уроку: засвоєння знань, умінь та навичок. Наочність і обладнання: набір демонстраційного креслярського приладдя. ХІД УРОКУ […]...
- ОЗНАЙОМЛЕННЯ З НАЗВАМИ ГЕОМЕТРИЧНИХ ТІЛ ОРІЄНТОВНА НАВЧАЛЬНА МЕТА: ОЗНАЙОМИТИ З НАЗВАМИ ГЕОМЕТРИЧНИХ ТІЛ; ЗАКРІПЛЮВАТИ ВМІННЯ РОЗВ’ЯЗУВАТИ ЗАДАЧІ НА РУХ; РОЗВИВАТИ ОБЧИСЛЮВАЛЬНІ НАВИЧКИ I. Перевірка домашнього завдання Фронтально з’ясувати, за якими правилами обчислили невідомі величини у вправі 518. У задачі 519 пояснити вибір дій. II. Актуалізація та корекція опорних знань учнів 1. Завдання для опитування. 1) За таблицею знайти невідомі значення […]...
- Властивості тригонометричних функцій УРОК 10 Тема. Властивості тригонометричних функцій Мета уроку: вивчення властивостей тригонометричних функцій у = sin х, у = cos х, у = tg х, у = ctg x (область визначення; область значень; парність (непарність); симетричність графіків; періодичність; нулі; проміжки спадання (зростання); проміжки знакопостійності; найбільші і найменші значення). І. Перевірка домашнього завдання Перевірити правильність побудови графіків […]...
- РЕГУЛЯЦІЯ ФУНКЦІЙ В ОРГАНІЗМІ – НЕЙРОГУМОРАЛЬНА РЕГУЛЯЦІЯ ФІЗІОЛОГІЧНИХ ФУНКЦІЙ – ЛЮДИНА Біологія – універсальний довідник ЛЮДИНА НЕЙРОГУМОРАЛЬНА РЕГУЛЯЦІЯ ФІЗІОЛОГІЧНИХ ФУНКЦІЙ РЕГУЛЯЦІЯ ФУНКЦІЙ В ОРГАНІЗМІ Для регуляції фізіологічних процесів відповідно до потреб організму і змін навколишнього середовища існує два механізми: гуморальний і нервовий. Гуморальна регуляція фізіологічних процесів здійснюється за допомогою хімічних речовин, які поступають із різних органів і тканин тіла у кров і розносяться нею по всьому […]...
- Знаки тригонометричних функцій Математика – Алгебра Тригонометричні функції Знаки тригонометричних функцій З означення тригонометричних функцій легко зробити висновок щодо знаків тригонометричних функцій у координатних чвертях: Зміна тригонометричних функцій при зростанні “a” від 0 до 2п Зміну , , , при зростанні від 0 до описано в табл. 2. Позначення: – зростає; – спадає....
- Лінійна функція та її графік Урок № 66 Тема. Лінійна функція та її графік Мета: сформувати свідоме розуміння учнями взаємозв’язку між взаємним розташуванням графіків двох лінійних функцій та співвідношенням їх кутових коефіцієнтів; виробити вміння: за даними рівняннями лінійних функцій робити висновки щодо взаємного розташування графіків; знаходити аналітичним способом координати точки перетину графіків двох лінійних функцій. Тип уроку: застосування знань, умінь […]...
- Властивості функцій – Функції та графіки Математика – Алгебра Функції та графіки Властивості функцій Функція називається Зростаючою на деякому проміжку, якщо більшому значенню аргументу із цього проміжку відповідає більше значення функції. Функція називається Спадною на деякому проміжку, якщо більшому значенню аргументу із цього проміжку відповідає менше значення функції. Якщо функція зростає (спадає) на всій області визначення, її називають зростаючою (спадною). Приклади […]...
- Приклади графіків залежностей між величинами Урок № 114 Тема. Приклади графіків залежностей між величинами Мета: формувати в учнів уявлення про зміст поняття “графік залежності”, сформувати уміння “читати таблиці” й виконувати побудову графіків простих залежностей за даними, розміщеними в таблиці Тип уроку: засвоєння нових знань Хід уроку I. Організаційний момент II. Перевірка домашнього завдання Збираємо зошити із творчими роботами на перевірку […]...
- ПОЗНАЧЕННЯ ГЕОМЕТРИЧНИХ ФІГУР БУКВАМИ ЛАТИНСЬКОГО АЛФАВІТУ. РОЗВ’ЯЗУВАННЯ І ПОРІВНЯННЯ ЗАДАЧ ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ. ЗАДАЧІ НА ДВІ ДІЇ. ВИРАЗИ З ДУЖКАМИ ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ Урок 18. ПОЗНАЧЕННЯ ГЕОМЕТРИЧНИХ ФІГУР БУКВАМИ ЛАТИНСЬКОГО АЛФАВІТУ. РОЗВ’ЯЗУВАННЯ І ПОРІВНЯННЯ ЗАДАЧ. (Розглядання двох задач, які мають спільну частину умови) Мета: вчити учнів позначати геометричні фігури буквами латинського алфавіту; розглянути і порівняти задачі, які мають спільну частину умови; […]...
- Висновки з перетворень Лоренца ФІЗИКА Частина 4 ОПТИКА. СПЕЦІАЛЬНА ТЕОРІЯ ВІДНОСНОСТІ Розділ 14 ШВИДКІСТЬ ПОШИРЕННЯ СВІТЛА. ОСНОВИ СПЕЦІАЛЬНОЇ ТЕОРІЇ ВІДНОСНОСТІ 14.6. Висновки з перетворень Лоренца Слід зазначити, що у формули перетворень Лоренца (14.9) і (14.10) входять не довжини відрізків і не проміжки часу, а координати окремих подій. Наприклад, час t відлічується за годинником, який перебуває в стані спокою в […]...
- Розв’язування рівнянь графічним способом Математика – Алгебра Функції Розв’язування рівнянь графічним способом За допомогою графіків функцій можна розв’язувати рівняння графічним способом. Для цього треба побудувати в одній системі координат графіки обох частин рівняння й знайти абсциси точок їх перетину. Приклад. Розв’яжіть рівняння . Побудуємо графіки функції і в одній координатної системі (див. рисунок) і знайдемо абсиси точок їх перетину. […]...
- Лінійна функція, її графік та властивості Урок № 65 Тема. Лінійна функція, її графік та властивості Мета: ознайомити учнів із “особливими випадками” лінійної функції і її графіком; узагальнити уяву учнів про зв’язок між k та b і графіком; подальше вдосконалювати вміння будувати й читати графіки лінійних функцій. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент (див. попередній урок) […]...
- Прості і складені задачі на визначення швидкості, часу і відстані. Дії над іменованими числами. Ознайомлення з назвами геометричних тіл Повторення вивченого (№№ 520-530) Тема. Прості і складені задачі на визначення швидкості, часу і відстані. Дії над іменованими числами. Ознайомлення з назвами геометричних тіл Повторення вивченого (№№ 520-530). Мета. Узагальнити зв’язки між відстанню, часом і швидкістю; закріплювати вміння учнів розв’язувати задачі на обчислення згаданих величин, виконувати дії над іменованими числами; ознайомити з назвами геометричних тіл. Обладнання. Таблиця усних обчислень; […]...
- Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і половинного аргументу УРОК 13 Тема. Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і половинного аргументу Мета уроку: вивчення формул тригонометричних функцій суми і різниці двох чисел, формул тригонометричних функцій подвійного і половинного аргументу. Формування умінь застосовувати вивчені формули для спрощення виразів та обчислень. І. Перевірка домашнього завдання Розв’язання вправ, аналогічних до домашніх: вправа […]...
- Властивості тригонометричних функцій – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Властивості тригонометричних функцій Функції У = sin x У = cos x Y = tg x 1. Область визначення Х (-∞;+∞) Х (-∞;+∞) X ≠ π/2 + πn, n Z 2. Множина значень Y Y Y (-∞;+∞) 3. Періодичність Усі тригонометричні функції – періодичні з найменшим додатним періодом Т […]...
- Інші комбінації геометричних тіл Геометрія Комбінації геометричних тіл Інші комбінації геометричних тіл Конус є вписаним у циліндр (див. рисунок нижче), коли основа конуса збігається з нижньою основою циліндра, а вершина конуса – центр верхньої основи циліндра. Осі циліндра і конуса в цьому випадку збігаються. Циліндр, вписаний у конус (див. рисунок нижче), якщо нижня основа циліндра лежить на основі конуса, […]...