Головна ⇒ 📌Довідник з геометрії ⇒ Поворот
Поворот
Геометрія
Рух
Поворот
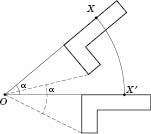
Поворотом площини навколо даної точки називається такий рух, при якому кожний промінь, що виходить із даної точки, повертається на один і той самий кут в одному й тому самому напрямку (див. рисунок).
Related posts:
- Поворот УРОК № 36 Тема. Поворот Мета уроку: формування поняття повороту та вивчення властивостей повороту; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур. Рухи” [13]. Вимоги до рівня підготовки учнів: описують поворот; будує фігури, у які переходять дані фігури при повороті; застосовують вивчені означення і […]...
- Властивості руху Геометрія Рух Якщо кожну точку даної фігури змістити деяким чином, то дістанемо нову фігуру. Кажуть, що ця фігура утворюється перетворенням даної. Перетворення однієї фігури в іншу називається Рухом, якщо це перетворення зберігає відстань між точками. Властивості руху 1. Два рухи, виконані послідовно, дають знову рух. 2. Перетворення, обернене до руху, є рух. 3. Під час […]...
- Перпендикуляр і похила Геометрія Стереометрія Перпендикуляр і похила Перпендикуляром, опущеним із даної точки на дану площину, називається відрізок, що сполучає дану точку з точкою площини й лежить на прямій, перпендикулярній до площини. Кінець цього відрізка, який лежить у площині, називається Основою перпендикуляра. Відстанню від точки до площини називається довжина перпендикуляра, опущеного із цієї точки на площину. На рисунку […]...
- Перпендикуляр Геометрія Основні властивості найпростіших геометричних фігур Перпендикуляр Дві прямі називаються Перпендикулярними, якщо вони перетинаються під прямим кутом (див. рисунок), тобто, коли вони перетинаються, утворюються чотири прямих кути. Позначення: . Теорема 1. Через кожну точку прямої можна провести перпендикулярну до неї пряму, і до того ж тільки одну. Перпендикуляром до даної прямої називається відрізок прямої, перпендикулярної […]...
- Коло Геометрія Основні властивості найпростіших геометричних фігур Коло Колом називається фігура, яка складається з усіх точок площини, рівновіддалених від даної точки. Ця точка називається Центром кола. Відстань від точок кола до його центра називається Радіусом кола. Радіусом також називається будь-який відрізок, що сполучає точку кола з його центром. Відрізок, що сполучає дві точки кола, називається Хордою. […]...
- Поворот і симетрія відносно прямої 373. Із т. А опустимо перпендикуляр AD + l. Відкладемо ∠ΑΟΛ, = α, А1O + l. Виконано поворот т. А навколо прямої l на кут α. Аналогічно вчинимо з т. В. Відрізок АВ у результаті повороту на кут α навколо прямої l відобразиться у відрізок. 374. Таких поворотів безліч. 375. Точка А(1; 2; 0) відобразиться […]...
- Антропологічний поворот у філософії та в спеціальних науках про людину Філософія світ людини Філософська антропологія та спеціальні науки про людину Антропологічний поворот у філософії та в спеціальних науках про людину Таким чином, у філософської антропології є, так би мовити, власна “оптика”, крізь яку здійснюється синтетичний розгляд людини, що поєднує в собі об’єктивно-науковий підхід із суб’єктно-реалістичною позицією. Така перспектива із необхідністю відбудовує структуру знань про людину […]...
- Означення. Аксіоми Геометрія Основні властивості найпростіших геометричних фігур Означення. Аксіоми Геометрія – це наука про властивості геометричних фігур. Зверніть увагу: геометрична фігура – це не тільки трикутник, коло, піраміда тощо, а й будь-яка множина точок. Планіметрія – це розділ геометрії, у якому вивчаються фігури на площині. Точка і Пряма є основними поняттями планіметрії. Це означає, що цим […]...
- Аксіоми стереометрії Геометрія Стереометрія Аксіоми стереометрії I. Яка б не була пряма, існують точки, що належать цій прямій, і точки, що не належать їй. Через будь-які дві точки можна провести пряму, й тільки одну. II. Із трьох точок на прямій одна й тільки одна лежить між двома іншими. III. Кожний відрізок має певну довжину, більшу від нуля. […]...
- Бісектриса Геометрія Основні властивості найпростіших геометричних фігур Бісектриса Бісектрисою кута називається промінь, який виходить із вершини кута, проходить між його сторонами й ділить кут пополам. На рисунку BD – бісектриса . Властивості бісектриси Теорема 1. Бісектриса кута утворює з його сторонами кути, не більші за . Теорема 2. Бісектриси вертикальних кутів лежать на одній прямій (тобто […]...
- ХІД ПРОМЕНІВ ЧЕРЕЗ ПЛОСКОПАРАЛЕЛЬНУ ПЛАСТИНКУ, ПРИЗМУ – ГЕОМЕТРИЧНА ОПТИКА Фізика підготовка до ЗНО комплексне видання КОЛИВАННЯ І ХВИЛІ. ОПТИКА 6. ОПТИКА 6.2. ГЕОМЕТРИЧНА ОПТИКА 6.2.4. ХІД ПРОМЕНІВ ЧЕРЕЗ ПЛОСКОПАРАЛЕЛЬНУ ПЛАСТИНКУ, ПРИЗМУ Хід променів у плоскопаралельній пластинці Після проходження через плоскопаралельну пластинку промені виходять під тим самим кутом, під яким вони на неї падають. При цьому пластинка зміщує промінь світла паралельно йому самому на відстань […]...
- Рівність фігур Геометрія Рух Рівність фігур Дві фігури називаються Рівними, якщо вони переводяться рухом одна в одну. Теорема. Рівні трикутники (означення дивись у розділі “Геометрія.”) є рівними фігурами, тобто суміщаються рухом....
- Геометричні фігури, точка, пряма, промінь Розділ 1. Елементарні геометричні фігури та їхні властивості § 1. Геометричні фігури, точка, пряма, промінь 1. 1) Прямій а належать точки А, В, С. 2) Прямій b належать точки Р i В. 3) Прямій а і прямій b належить точка В. 4) Точки А і С належать прямій а, але не належать прямій b. 5) […]...
- Промінь. Кут. Вимірювання кутів § 1. Найпростіші геометричні фігури та їхні властивості 3. Промінь. Кут. Вимірювання кутів Практичні завдання 49. Промені AB і АС – не доповняльні. Промінь AN – доповняльний до променя AB, а промінь AM – доповняльний до променя АС. На рисунку зображено промені АB, АС, AN, AM. 50. Промені AB і ВА не е доповняльними, оскільки […]...
- ЛІЧБА, ВИМІРЮВАННЯ І ЧИСЛА ЗАДАЧІ НА ПОВТОРЕННЯ ЛІЧБА, ВИМІРЮВАННЯ І ЧИСЛА 1. Скільки чисел натурального ряду розміщено між числами: 1)120 і 129; 2) 999 і 1100; 3)8901 і 8910; 4) 50000 і 50020? 2. На прямій дано три точки А, В і С. Знайдіть довжину відрізка ВС, якщо АВ = 8 см і АС – 9 см. Скільки розв’язків […]...
- Координатні промені і шкали Урок № 17. Тема. Координатні промені і шкали Мета. Формувати уміння та навички учнів накреслити координатний промінь, позначати точки із координатами, визначати ціну поділки. Розвивати уяву, виховувати охайність та відповідальність. Обладнання: кодоскоп. Хід уроку І. Організація класу. ІІ. Перевірка домашнього завдання. 1.Фронтальне опитування: А) що таке координатний промінь? Б) що таке координата точки координатного променя? […]...
- Геометричне місце точок Геометрія Основні властивості найпростіших геометричних фігур Геометричне місце точок Геометричним місцем точок (ГМТ), які мають певну властивість, називається така фігура, що складається з усіх точок площини, які мають цю властивість, і тільки з них. Довести, що фігура М є ГМТ, які мають властивість Р, означає довести два такі твердження. 1. Якщо точка А ∈ М, […]...
- Числовий промінь Математика – Алгебра Числовий промінь Накреслимо промінь Оx горизонтально праворуч від точки О. Проти початку променя напишемо число 0. Відкладемо від 0 довільний відрізок, який приймемо за одиницю, назвемо його Одиничним відрізком. Поставимо у відповідність кожній точці променя число, яке виражає відстань від 0 до цієї точки, виміряну в одиничних відрізках, і назвемо таке число […]...
- Нерівність трикутника Геометрія Трикутники Нерівність трикутника Теорема. Які б не були три точки, відстань між будь-якими двома із цих точок не більша, ніж сума відстаней від них до третьої точки. Звідси випливає, що у будь-якому трикутнику кожна сторона менша за суму двох інших сторін, але більша за модуль різниці двох інших сторін. Якщо a, b і c […]...
- Перетворення в просторі – Декартові координати та вектори в просторі Геометрія Декартові координати та вектори в просторі Перетворення в просторі Поняття перетворення для фігур у просторі означають так само, як і на площині (див. розділ “Геометрія. 8 клас”). Рухом Називається перетворення, при якому зберігаються відстані між точками. Властивості руху в просторі: Прямі переходять у прямі, півпрямі – у півпрямі, відрізки – у відрізки, кути між […]...
- Відстань між точками Геометрія Декартові координати на площині Відстань між точками Якщо , – довільні точки і AB відстань між ними, то або . У випадку, коли точка B збігається з початком координат , отримуємо: . Рівнянням фігури на площині в декартових координатах називається рівняння з двома змінними x і y, яке задовольняють координати будь-якої точки фігури й […]...
- Симетрія відносно точки Геометрія Рух Симетрія відносно точки Нехай O – фіксована точка, X – довільна точка площини. Відкладемо на продовженні відрізка OX за точку O відрізок , що дорівнює OX. Точка називається Симетричною точці X відносно точки O (див. рисунок). Очевидно, що точка, симетрична , є точка X. Перетворення фігури F у фігуру , при якому кожна […]...
- Перпендикуляр до прямої Урок № 19 Тема. Перпендикуляр до прямої Мета: домогтися розуміння учнями змісту теореми про існування та єдиність прямої, що проходить через будь-яку точку площини перпендикулярної даній; понять: “перпендикуляр, проведений з точки до прямої”, “відстані від точки до прямої”. Сформувати вміння: – відтворювати зміст зазначеної теореми та застосовувати її під час розв’язування задач; – на рисунку […]...
- КУТИ І ЇХ МІРИ РОЗДІЛ 1 НАЙПРОСТІШІ ГЕОМЕТРИЧНІ ФІГУРИ ТА ЇХ ВЛАСТИВОСТІ & 3. КУТИ І ЇХ МІРИ Два промені, що мають спільний початок, розбивають площину на дві частини. Частину площини, обмежену двома променями із спільним початком, називають кутом. Промені, що обмежують кут, називають сторонами кута, а їх спільний початок – вершиною кута (мал. 30, а). Такий кут називають […]...
- Циліндр, вписаний у кулю Геометрія Комбінації геометричних тіл Циліндр, вписаний у кулю Основи циліндра є рівновіддаленими від центра кулі (рисунок нижче зліва). Ця комбінація тіл є симетричною відносно будь-якої площини, що проходить через центр кулі паралельно твірним циліндра. У перерізі тіла такою площиною дістанемо прямокутник і описане навколо нього коло (рисунок справа). Прямокутник ABCD є осьовим перерізом циліндра, а […]...
- ТОЧКИ І ПРЯМІ РОЗДІЛ 1 НАЙПРОСТІШІ ГЕОМЕТРИЧНІ ФІГУРИ ТА ЇХ ВЛАСТИВОСТІ У цьому розділі ви повторите і поглибите свої знання про найпростіші і найважливіші геометричні фігури: точки, прямі, відрізки, кути. Дізнаєтесь, як вимірюють відрізки і кути, ознайомитесь із найуживанішими креслярськими і вимірювальними інструментами. & 1. ТОЧКИ І ПРЯМІ Геометрія – це наука про геометричні фігури та їх властивості. […]...
- Промінь, пряма, площина Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 17. Промінь, пряма, площина Продовжимо відрізок АВ за допомогою лінійки за точку В (рис. 38). На рисунку таке продовження обмежене розмірами аркуша, але можна уявити, що ми продовжили відрізок необмежено. Якщо продовжити відрізок АВ за його кінець В необмежено, то одержимо промінь […]...
- ПРИНЦИП СПІВІСНУВАННЯ Екологія – охорона природи ПРИНЦИП СПІВІСНУВАННЯ, “парадокс Дж. Хатчинсона” – два види можуть співіснувати в одній екол. ніші, і якщо близькі види змушені використовувати одні й ті самі ресурси, то прир. добір може сприяти їхньому існуванню і вони здатні еволюціонувати в одному й тому самому напрямку. П. с. протилежний принципу виключення Г. Ф. Гаузе. Він […]...
- Тригранний і многогранний кути Геометрія Многогранники Тригранний і многогранний кути Нехай промені a, b, c виходять з однієї точки й не лежать в одній площині. Тригранним кутом називається фігура, яка складається з трьох плоских кутів , , (див. рисунок). Ці кути називаються Гранями тригранного кута, а їх сторони – Ребрами. Спільна вершина плоских кутів називається Вершиною тригранного кута. Двогранні […]...
- МОНОКУЛЬТУРА Екологія – охорона природи МОНОКУЛЬТУРА – 1) беззмінне багаторічне вирощування однієї с.-г. культури на одному й тому самому полі; 2) поля (або ін. с.-г. території), зайняті одним видом культ, рослин....