Головна ⇒ 📌Формули й таблиці ⇒ Похідна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ
Похідна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ
Формули й таблиці
МАТЕМАТИКА
ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ
Похідна функція
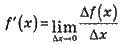 – визначення похідної функції.
– визначення похідної функції.
Рівняння дотичної до графіка функції y = f(x) у точці М(х0,у0):
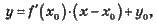
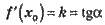 – кутовий коефіцієнт дотичної.
– кутовий коефіцієнт дотичної.
Related posts:
- Первісна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Первісна функція Первісною для даної функції y = f(x) на проміжку (а; b) називається така функція F(x), похідна якої для всіх х (а;b), що дорівнює f(x): F'(x) = f(x). Загальний вигляд первісної F(x) + C, де С – довільне стале число. Теорема. Будь-яка неперервна на функція y = f(x) […]...
- Показникова функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Показникова функція У = ах (0 < а < 1) У = ах (а > 1) Область визначення Х (-∞;+∞) Х (-∞;+∞) Множина значень Y (0;+∞) Y (0;+∞) Перетин з віссю Y При х = 0, y = 1. При х = 0, y = 1. Монотонність Функція спадає […]...
- Логарифмічна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Логарифмічна функція Y = logax(0 < a < 1) У = logax(а > 1) Область визначення Х (0;+∞) Х (0;+∞) Множина значень Y (-∞;+∞) Y (-∞;+∞) Перетин з осями координат З віссю ОХ Х = 1, у = 0; Х = 1, у = 0; З віссю OY Перетину […]...
- Властивості тригонометричних функцій – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Властивості тригонометричних функцій Функції У = sin x У = cos x Y = tg x 1. Область визначення Х (-∞;+∞) Х (-∞;+∞) X ≠ π/2 + πn, n Z 2. Множина значень Y Y Y (-∞;+∞) 3. Періодичність Усі тригонометричні функції – періодичні з найменшим додатним періодом Т […]...
- Обернені тригонометричні функції – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ У = sin x 0; π/2 π/2 π/2; π π π; 3π/2 3π/2 3π/2; 2π 2π M A X П E P E Т И Н И M I N П E P E Т И Н И У = cos x 0; π/2 π/2 π/2; π π π; […]...
- Обернені функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Обернені функції Дві функції називаються оберненими, якщо вони виражають ту саму залежність між змінними величинами, але в одній з них за аргумент прийнято х, а за функцію – у, в іншій – навпаки, тобто за аргумент прийнято у, а за функцію – х. Функції у = f(x) […]...
- Похідна Математика – Алгебра Похідна Похідною функції в точці називається границя відношення приросту функції до приросту аргументу за умови, що границя існує, а приріст аргументу прямує до нуля, тобто . Функція в точці називається Диференційовною, якщо в цій точці вона має похідну . Якщо функція є диференційовною в кожній точці деякого інтервалу , то вона називається […]...
- Формули приведення – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули приведення π/2 ± α π ± α 3 π/2 ± α 2π ± α 90° ± α 180° ± α 270° ± α 360° ± α Sin β Cosα Sinα -cosα ±sinα Cos β Sinα -cosα ±sinα Cosα Tg β Tgα ctgα Tgα Tgα ctgα ±tgα Ctg β […]...
- Значення функцій деяких кутів – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Значення функцій деяких кутів α 0; 2π π/6 π/4 π/3 π/2 π 3π/2 0; 360° 30° 45° 60° 90° 180° 270° Sin α 0 1/2 /2 /2 1 0 -1 Cos α 1 /2 /2 1/2 0 -1 0 Tg α 0 1/ 1 Не існують 0 Не існують […]...
- Основні тригонометричні тотожності – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Основні тригонометричні тотожності...
- Обернені тригонометричні функції: у = arcsin х, у = arccos х УРОК 18 Тема. Обернені тригонометричні функції: у = arcsin х, у = arccos х Мета уроку: вивчення властивостей обернених тригонометричних функцій: у = arcsin х, у = arccos х. І. Перевірка домашнього завдання Математичний диктант. Закінчіть математичні твердження: 1. Функція, яка набуває кожного свого значення в єдиній точці області визначення називається… 2. Оберненою до функцій […]...
- Похідна та її застосування 127. 1) 2) 3) 4) 128. 1) Y = φ(x), 2) У = φ(x), не існує; 3) φ(1) = 0. 129. 1) f(x) = x2 + 1, x0 = -1, Δx = 0,1; Δy – ? Δy = у(х0 + Δх) – у(х0) = f( -0,9) – f(-1) = (-0,9)2 + 1 – ((-1)2 + […]...
- Дослідження властивостей функції і побудова її графіка Математика – Алгебра Похідна Дослідження властивостей функції і побудова її графіка Для того щоб дослідити функцію , треба: 1) знайти область визначення ; 2) знайти область значень ; 3) дізнатися про парність чи непарність функції ; 4) з’ясувати, чи є функція періодичною; 5) знайти нулі функції; точки перетину графіка з осями координат; 6) визначити проміжки, […]...
- Правила диференціювання – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Правила диференціювання Правило 1. Якщо функції у = f(x) і у = g(x) мають похідну в точці х, то і їх сума має похідну в точці х, до того ж похідна суми дорівнює сумі похідних: Правило 2. Якщо функція у = f(x) має похідну в точці х, то і […]...
- Тригонометричні функції числового аргументу Математика – Алгебра Тригонометричні функції Тригонометричні функції числового аргументу Розглянемо одиничне (тригонометричне) коло, центр якого розташований у точці і радіус якого дорівнює 1 (див. рисунок). Нехай точка P0 – це точка (1; 0). Кожну іншу точку кола можна дістати поворотом P0 навколо початку координат. Будемо вважати від’ємним напрямок повороту за годинниковою стрілкою, додатним – проти. […]...
- Арифметичні операції над диференційовними функціями Математика – Алгебра Похідна Арифметичні операції над диференційовними функціями Теорема 1. Якщо функції і в точці мають похідні, то функція в цій точці також має похідну, яка дорівнює . Теорема 2. Якщо функції і в точці мають похідні, то в цій точці функція також має похідну, яка дорівнює . Наслідок. Якщо функція має похідну в […]...
- Функції та їхні властивості. Квадратична функція УРОК № 62 Тема. Функції та їхні властивості. Квадратична функція Тестові завдання 1. Знайдіть область визначення функції . А) х 5; Б) х -5; В) х -5, х 0; Г) х 3, х -5, х 0. 2. Знайдіть нулі функції . А) 0; 2; б) 2; в) 0; -2; г) нулів немає. 3. Яка з […]...
- Обернені тригонометричні функції: у = arctg x, у = arcctg x УРОК 19 Тема. Обернені тригонометричні функції: у = arctg x, у = arcctg x Мета уроку: вивчення властивостей обернених тригонометричних функцій: у = arctg х і у = arcctg x. І. Перевірка домашнього завдання 1. Фронтальна бесіда з класом за питаннями 6, 7, 9-12, до “Запитання і завдання для повторення” розділу II. 2. Самостійна робота. […]...
- Степеневі функції з раціональними показниками – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Степеневі функції з раціональними показниками...
- Степеневі функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Степеневі функції Графіки функції є параболами степеня n Графіки функції є гіперболами Функція y = ах, де а > 0, а ≠ 1, називається показниковою функцією з основою а. Приклад 0 < а < 1 Y = (1/2)x А > 1 Y = 2х Область визначення Х […]...
- Квадратичні функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Квадратичні функції Графіком квадратичної функції є парабола, яка отримується з графіка функції у = ах2 за допомогою двох паралельних перенесень: – перенесення уздовж осі ОХ на m одиниць ліворуч, якщо m < 0, і праворуч, якщо m > 0; – перенесення уздовж осі OY на у0 одиниць […]...
- Схема дослідження – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Функцією (або функціональною залежністю) називається закон, за яким кожному значенню незалежної змінної х з деякої множини чисел, що називається областю визначення функції, ставиться у відповідність тільки одне певне значення величини у. Графіком функції називається множина всіх точок координатної площини з координатами (х, у), такими, при яких абсциса […]...
- Теорема Вієта – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Теорема Вієта Щоб числа x1 та х2 були розв’язками рівняння ах2 + bх + с = 0, необхідно й достатньо, щоб:...
- Основні тригонометричні рівняння – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Основні тригонометричні рівняння Sin x = 0 X = πk, k Z Cos x = 0 X = π/2 + 2πk, k Z Sin x = 1 X = π/2 + 2πk, k Z Cos x = 1 X = 2πk, k Z Sin x = -1 X […]...
- Функції та графіки. Лінійна функція Урок № 67 Тема. Функції та графіки. Лінійна функція Мета: повторити та узагальнити відомості щодо змісту основних понять теми; повторити, систематизувати набуті практичні вміння; провести підготовку до тематичної контрольної роботи. Тип уроку: узагальнення та систематизація знань, умінь, навичок. Хід уроку I. Організаційний момент 1. Готовність до уроку. 2. План роботи на уроці. II. Перевірка домашнього […]...
- Лінійні функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Лінійні функції...
- Неперервність функції в точці Математика – Алгебра Границя Неперервність функції в точці Нехай функція визначена на проміжку і точка є внутрішньою точкою цього проміжку. Функція називається Неперервною в точці, якщо існує границя функції в цій точці й вона дорівнює значенню функції в точці . Нехай функція визначена в усіх точках деякого проміжку . Візьмемо дві довільні точки з цього […]...
- Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і половинного аргументу УРОК 13 Тема. Формули тригонометричних функцій суми і різниці двох чисел. Тригонометричні функції подвійного і половинного аргументу Мета уроку: вивчення формул тригонометричних функцій суми і різниці двох чисел, формул тригонометричних функцій подвійного і половинного аргументу. Формування умінь застосовувати вивчені формули для спрощення виразів та обчислень. І. Перевірка домашнього завдання Розв’язання вправ, аналогічних до домашніх: вправа […]...
- Підсумковий урок з теми “Функції. Властивості функції. Функція у = ах2+bx+c. Розв’язування квадратних нерівностей” УРОК № 26 Тема. Підсумковий урок з теми “Функції. Властивості функції. Функція у = ах 2 + b х + С. Розв’язування квадратних нерівностей” Мета уроку: повторити, систематизувати й узагальнити знання та вміння учнів щодо змісту вивчених у розділі “Функція та її властивості” понять і схем розв’язування типових задач шляхом складання загальних алгоритмів розв’язування задач. […]...
- Квадратична функція – Функції та графіки Математика – Алгебра Функції та графіки Квадратична функція Квадратним тричленом називається многочлен виду , де x – змінна, a, b і c – деякі числа, причому . Коренем квадратного тричлена називається таке значення змінної, яке перетворює квадратний тричлен на 0. Щоб знайти корені квадратного тричлена, треба розв’язати квадратне рівняння . Теорема. Якщо і – корені […]...