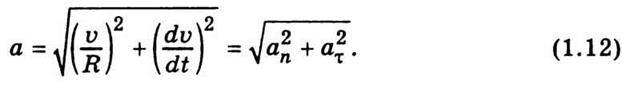Прискорення. Прискорення при криволінійному русі – КІНЕМАТИКА
ФІЗИКА
Частина 1 МЕХАНІКА
Розділ 1 КІНЕМАТИКА
1.3. Прискорення. Прискорення при криволінійному русі
Градієнт швидкості матеріальної точки V з часом £ характеризують прискоренням
Прискорення виражається в метрах на секунду в квадраті (СІ) та сантиметрах на секунду в квадраті (СГС).
При прямолінійному русі вектор швидкості напрямлений уздовж однієї й тієї самої прямої – траєкторії, внаслідок чого напрям вектора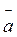 
збігається з напрямом вектора 
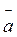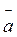збігається за напрямом із , то швидкість збільшується і рух буде прискореним. Якщо протилежне за напрямом до , то швидкість зменшується і рух буде сповільненим.Прямолінійний рух зі сталим прискоренням називають рівнозмінним. Залежно від зміни швидкості в часі розрізняють рівномірно прискорений та рівномірно сповільнений рухи. При рівнозмінному прямолінійному русі справедлива формула
Де – швидкість у момент часу t;
0- швидкість у початковий момент часу (при t = 0); 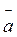– прискорення. При цьому вектори , 0, 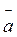напрямлені вздовж однієї прямої.Визначимо прискорення точки у разі її руху по криволінійній траєкторії (рис. 1.2). Нехай у момент часу t точка була в положенні А, а в момент часу t + Δt – у положенні В. Швидкості 1і 2 у точках А і В напрямлені по дотичних до траєкторії в цих точках. Перенесемо вектор 2 в точку А. Зміна швидкості за проміжок часу Δt визначиться вектором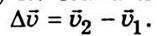 
Із рис. 1.2. бачимо, що
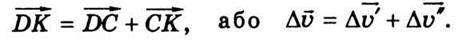
Тоді прискорення в точці А запишемо так:
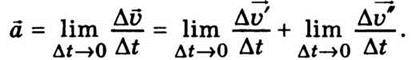
Вектор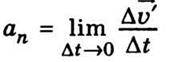 
Називають нормальним прискоренням, а вектор 
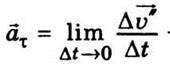– тангенціальним. Прискорення 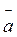N перпендикулярне до вектора швидкості 1 і завжди напрямлене до центра кривизни. Звідси й назва цього вектора – нормальний (тобто перпендикулярний).
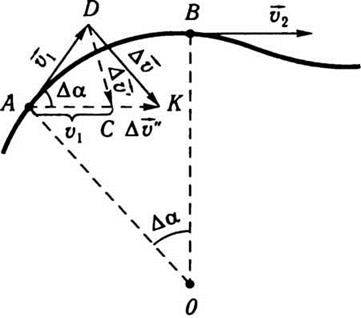
Рис. 1.2.
Визначимо модуль нормального прискорення. Як видно з рис. 1.2, для малого кута Δα можна записати
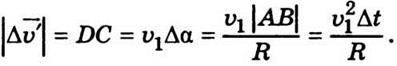
Тоді
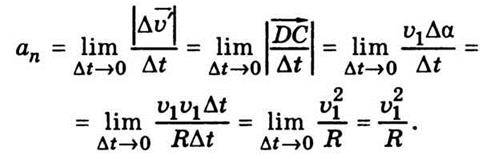
Отже, модуль 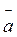П у деякій точці траєкторії дорівнює відношенню квадрата швидкості до радіуса кривизни траєкторії в цій самій точці:
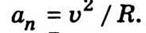
Якщо на нормалі до траєкторії відкласти в точці А одиничний вектор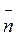 
, що напрямлений до центра кривизни, то вектор нормального прискорення можна записати так:
Розглянемо тепер вектор тангенціального прискорення
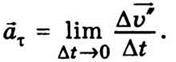
Зазначимо, що модуль вектора Δ‘ дорівнює за абсолютною величиною різниці модулів 2 та 1 (див. рис. 1.2). Тоді
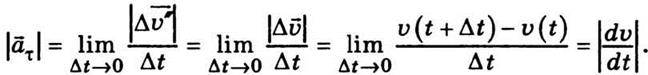
Відповідно тангенціальне прискорення
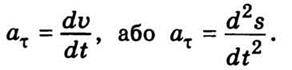
Отже, значення тангенціального прискорення дорівнює першій похідній від швидкості за часом або другій похідній_від шляху. Напрям вектора 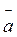τ визначається напрямом вектора Δ‘, який він набуває в граничному випадку, коли Δt -> 0. Неважко побачити, що в граничному випадку вектор Δ‘ напрямлений по дотичній до траєкторії в точці А. Звідси і назва цього вектора – тангенціальний (дотичний). Якщо ввести одиничний вектор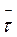 
, дотичний до траєкторії і напрямлений у бік руху точки, то вектор тангенціального прискорення можна записати так:
Вектор 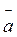τ показує, як змінюється швидкість за числовим значенням, а вектор 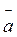N характеризує зміну швидкості за напрямом. Отже, для повного прискорення запишемо
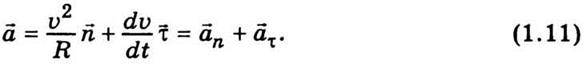
Модуль вектора загального прискорення знайдемо із співвідношення
