ПРОСТІ МЕХАНІЗМИ. КОЕФІЦІЄНТ КОРИСНОЇ ДІЇ МЕХАНІЗМІВ

РОЗДІЛ 4 МЕХАНІЧНА РОБОТА ТА ЕНЕРГІЯ

& 36. ПРОСТІ МЕХАНІЗМИ. КОЕФІЦІЄНТ КОРИСНОЇ ДІЇ МЕХАНІЗМІВ

Прості механізми – це трудівники зі “стажем роботи” понад 30 століть, проте вони анітрохи не “постаріли”, адже в кожному сучасному технічному пристрої обов’язково знайдеться простий механізм, і не один. Ці пристрої дозволяють змінити напрямок дії сили, отримати виграш у силі або відстані. А чи дають вони виграш у роботі?

1. Знайомимося з важливою характеристикою простих механізмів

Ви вже знаєте, що важелі з різними

плечима та рухомі блоки дозволяють отримати виграш у силі, однак такий виграш дається не “задарма”, адже, отримавши перевагу в силі, ми обов’язково програємо у відстані (рис. 36.1). Давнє так зване “золоте правило” механіки стверджує: “У скільки разів ми виграємо в силі, у стільки ж разів програємо у відстані”. А чи дійсно це так?

Припустимо, що треба підняти вантаж на певну висоту. Щоб було зручніше, скористаємося нерухомим блоком. Для цього слід перекинути через блок мотузку, прив’язати до неї вантаж і, взявшись за вільний кінець мотузки, рівномірно тягти мотузку вниз (рис. 36.2).

Нерухомий блок

можна уявити як рівноплечий важіль, тому сила, з якою тягнуть мотузку, має дорівнювати вазі вантажу: F = P. Однак на практиці обертанню блока завжди заважає сила тертя, тому, щоб підняти вантаж, до вільного кінця мотузки слід прикласти силу, більшу за вагу вантажу: F > P (див. рис. 36.2).

Так, при підніманні вантажу на висоту h виконується корисна робота:

Акор = Ph.

А от повна робота, тобто робота, яку виконує вантажник, витягаючи мотузку на довжину, що дорівнює висоті h, обчислюється за формулою:

Аповна = Fh.

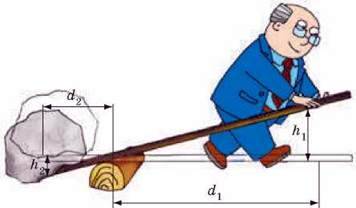
Рис. 36.1. Діючи на довге плече d1 важеля, ми виграємо в силі. Але висота h1 на яку ми маємо опустити плече d2 буде більшою від висоти h2, на яку підніметься тіло, у стільки разів, у скільки плече d1 довше за плече d2

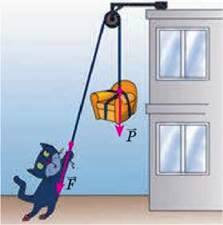
Рис. 36.2. Якщо в блоці є тертя, то сила F, з якою тягнуть мотузку, за значенням більша за вагу P вантажу

Оскільки F > P, то повна робота більша за корисну.

Корисна робота, яку виконують за допомогою будь-якого механізму, завжди менша за повну роботу: Акор < Аповна. Тільки за ідеальних умов корисна робота може дорівнювати повній роботі, але цього ніколи не буває.

Яку частину повної роботи механізм перетворює на корисну, показує фізична величина, яку називають коефіцієнт корисної дії (ККД).

Коефіцієнт корисної дії (ККД) механізму – це фізична величина, яка характеризує механізм і дорівнює відношенню корисної роботи до повної роботи:

η = .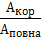

Коефіцієнт корисної дії (ККД) позначають символом п (ета). Зазвичай ККД подають у відсотках:

η = 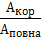∙ 100%

Оскільки в ході використання механізмів корисна робота завжди менша від повної, ККД будь-якого механізму завжди менший від 100 %.

2. Досліджуємо похилу площину

Окрім важеля та блока людина з античних часів використовує ще один простий механізм – похилу площину (рис. 36.3). За допомогою похилої площини можна піднімати важкі предмети, прикладаючи до них відносно невелику силу.

Дістанемо формулу для визначення ККД похилої площини. Нехай треба підняти тіло масою m на висоту h похилою площиною завдовжки l (рис. 36.4).

Щоб підняти тіло вертикально (без похилої площини), потрібно прикласти до нього силу 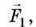яка за значенням дорівнює силі тяжіння:

F1 = Fтяж = mg.

Тіло необхідно підняти на висоту h, тому корисна робота дорівнюватиме: Акор = F1h = mgh (тобто дорівнюватиме збільшенню потенціальної енергії вантажу).

Щоб затягти тіло похилою площиною на ту саму висоту h, слід прикласти силу тяги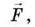 напрямлену вздовж похилої площини. Робота, яка при цьому виконується (повна робота), обчислюється за формулою: Аповна = Fl, де l – довжина похилої площини.

За означенням ККД маємо:

η = = .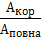

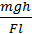Поміркуйте, як можна збільшити ККД похилої площини.

Руху тіла похилою площиною заважає сила тертя. У разі відсутності тертя між тілом і похилою площиною корисна робота дорівнювала б повній роботі: Акор = Аповна, тобто F1h =Fl (див. рис. 36.4). У такому випадку ми отримали б найбільший виграш у силі:

= .

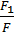Властивість похилої площини давати виграш у силі та змінювати напрямок дії цієї сили застосовують у використанні сходів, ескалаторів, конвеєрів, пандусів тощо (рис. 36.5).

Рис. 36.3. Похила площина є незамінною, коли треба підняти вантаж. Чим пологіший ухил площини, тим легше виконати цю роботу

3. Знайомимося з різновидами похилої площини

Одним із різновидів похилої площини є клин. Так, щоб полегшити рубання дров, у тріщину колоди вставляють клин і б’ють по ньому обухом сокири (рис. 36.6). Під час удару на клин діють три тіла: зверху – обух сокири, з боків – дві частини колоди.

Відповідно клин діє на обух сокири вгору, а на деревину колоди – в боки, тобто розсуває половинки колоди. Таким чином, клин змінює напрямок сили сокири. Крім того, кожна з двох сил, з якими клин розсуває половинки колоди, набагато більша за силу удару сокири.

Різновидом похилої площини також є гвинт. Візьмемо трикутник, вирізаний із тонкого картону, та розташуємо його біля циліндра (рис. 36.7). Похилою площиною слугуватиме ребро картону. Обгорнувши картонний трикутник навколо циліндра, одержимо гвинтову похилу площину. Власне, нарізка гвинта – це похила площина, яку багато разів обернуто навколо циліндра. Подібно до клина гвинт може змінювати напрямок і значення прикладеної сили.

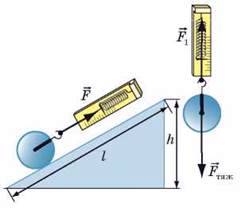
Рис. 36.4. Для втягування тіла вгору похилою площиною потрібна значно менша сила, ніж для підняття цього самого тіла вертикально

Рис. 36.5. Ескалатор є прикладом використання властивостей похилої площини

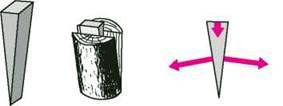
Рис. 36.6. Клин не тільки дає виграш у силі, але й змінює її напрямок

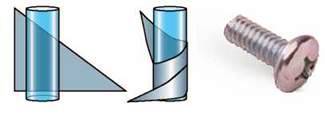
Рис. 36.7. Різновидом похилої площини є гвинт

Принцип дії гвинта використовують у багатьох механізмах і пристроях: механічних домкратах і підйомниках, м’ясорубці, лещатах, струбцинах, свердлах, шурупах, різьбових кріпленнях тощо.

Які властивості гвинтової похилої площини ми використовуємо, піднімаючись гірськими “серпантинами”? гвинтовими сходами?

4. Учимося розв’язувати задачі

Зверніть увагу! Якщо в задачі дано ККД або пропонується його знайти, розв’язання краще починати із запису формули для ККД. В умові значення ККД краще подавати в частках (тобто користуватися формулою η = 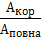), а у відповіді краще записувати у відсотках.

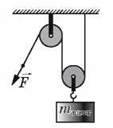
Задача. Вантаж масою 95 кг рівномірно піднімають на третій поверх будинку за допомогою рухомого та нерухомого блоків (див. Малюнок). Визначте ККД цієї системи, якщо до вільного кінця мотузки прикладають силу 500 Н.

Аналіз фізичної проблеми. Для визначення ККД системи слід знайти: роботу, яку необхідно виконати, щоб підняти вантаж на висоту h, тобто корисну роботу Акор; роботу, яку виконують, коли тягнуть мотузку, діючи на неї з певною Силою 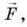тобто повну работу Аповн. У системі є один рухомий блок, тому програш у відстані становіть 2 рази: піднімаючи вантаж на висоту h, мотузку витягують на довжину l = 2h. Нерухомий блок системи тільки змінює напрямок дії сили.

Дано:

Mвант = 95 кг

F = 500 Н

G = 10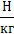

Знайти:

η – ?

Пошук математичної моделі. Розв’язання. За означенням ККД:

η =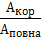

Що роблять? Піднімають вантаж на висоту h, тому корисна робота дорівнює збільшенню потенціальної енергії вантажу:

Акор = mвантgh.

Як це роблять? Тягнуть за мотузку, прикладаючи силу F. Тому повна робота, яку виконують для підняття вантажу, становить: Аповна = Fl, де l = 2h. Отже:

Fповна = F ∙ 2h.

Підставивши вирази для Акор і Аповна у формулу ККД, маємо:

η = = .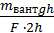

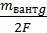Перевіримо одиницю, визначимо значення шуканої величини:

[η] = 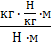= 1; η = 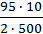= = 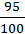0,95; η = 95%.

Аналіз результату: ККД механізму менший від 100 % – це правдоподібний результат.

Відповідь: η = 95%.

Підбиваємо підсумки

Для полегшення праці люди з давніх часів використовували прості механізми – пристрої для перетворення сили. Прості механізми – неодмінні складові й сучасних машин. До простих механізмів належать важіль і його різновиди (рухомий і нерухомий блоки, коловорот); похила площина та її різновиди (клин, гвинт).

На практиці корисна робота, яку виконують за допомогою будь-якого механізму, завжди є меншою від повної роботи:

Акор < Аповна.

Фізична величина, яка характеризує механізм і дорівнює відношенню корисної роботи до повної роботи, називається коефіцієнтом корисної дії механізму:

η = .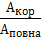

Зазвичай ККД подають у відсотках:

η = 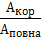∙ 100%.

ККД будь-якого механізму завжди менший від 100 %.

Контрольні запитання

1. Для чого використовують прості механізми? 2. Чому на практиці корисна робота завжди менша від повної роботи? 3. Дайте означення ККД. 4. Як визначити ККД похилої площини? 5. Назвіть різновиди похилої площини. 6. Наведіть приклади використання простих механізмів у сучасних машинах.

Вправа № 36

1. Двигун підіймального крана виконав повну роботу 1 кДж. Чи може корисна робота дорівнювати: а) 1530 Дж; б) 1000 Дж; в) 900 Дж?

2. За допомогою простого механізму виконано корисну роботу 120 Дж. Визначте ККД механізму, якщо повна робота дорівнює 150 Дж.

3. Тіло піднімають похилою площиною, виконуючи корисну роботу 180 кДж. Визначте повну роботу, якщо ККД похилої площини 90 %.

4. Тіло піднімають похилою площиною, прикладаючи в напрямку руху тіла силу 50 Н. Визначте масу тіла, якщо довжина похилої площини дорівнює 2 м, її висота – 50 см, а ККД становить 80 %.

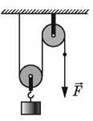
5. Вантаж масою 45 кг піднімають за допомогою пристрою, який складається з рухомого та нерухомого блоків (див. Малюнок). Яку силу потрібно прикладати до вільного кінця мотузки, якщо ККД пристрою становить 75 %?

6. Вантаж масою 108 кг підняли за допомогою важеля, прикладаючи вертикальну силу 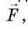значення якої до рівнює 400 Н. Визначте ККД важеля, якщо плече сили, яка діє на важіль з боку вантажу, втричі менше від плеча сили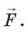

7. Скориставшись додатковими джерелами інформації, дізнайтеся про значення ККД деяких механізмів і про роботу, яку вони виконують. Складіть 1-2 задачі за отриманими даними, розв’яжіть їх.

Експериментальне завдання

Огляньте побутову м’ясорубку. Які прості механізми входять до її складу?

Відеодослід. Перегляньте відеоролик і поясніть спостережуване явище.

ЛАБОРАТОРНА РОБОТА № 12

Тема. Визначення ККД похилої площини.

Мета: переконатися на досліді, що корисна робота, виконана за допомогою похилої площини, менша від повної роботи; визначити ККД похилої площини.

Обладнання: мірна стрічка; динамометр; три тягарці однакової маси; дерев’яна лінійка; штатив із муфтою та лапкою; дерев’яний брусок.

ВКАЗІВКИ ДО РОБОТИ

Підготовка до експерименту

1. Перед тим як виконувати роботу, згадайте відповіді на такі запитання.

1) Які види простих механізмів ви знаєте?

2) Як визначити коефіцієнт корисної дії?

3) Чому ККД будь-якого механізму завжди менший від 100 %?

2. Визначте ціни поділок шкал вимірювальних приладів.

3. Зберіть експериментальну установку, як показано на рисунку.

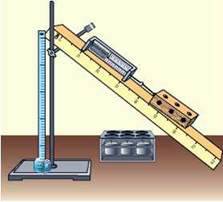
Експеримент

Суворо дотримуйтесь інструкції з безпеки (див. форзац підручника). Результати вимірювань відразу заносьте до таблиці.

1. Виміряйте за допомогою мірної стрічки довжину l і висоту h похилої площини.

2. Визначте за допомогою динамометра вагу Р1 бруска.

3. Покладіть брусок на похилу площину і за допомогою динамометра рівномірно пересувайте його площиною вгору. Виміряйте силу тяги F1 що діє на брусок з боку динамометра.

4. Визначте за допомогою динамометра вагу одного тягарця.

5. Не змінюючи кута нахилу площини, повторіть дослід (див. п. 3) ще тричі, розмістивши на бруску спочатку один, потім два, а потім три тягарці.

Зверніть увагу! У кожному з цих дослідів, щоб знайти вагу тіла, слід до ваги бруска додати вагу тягарця (тягарців).

Опрацювання результатів експерименту

1. Для кожного досліду обчисліть:

1) повну роботу (Аповна = Fl);

2) корисну роботу (Акор = Ph, де P – вага тіла)

3) виграш у силі, який дає похила площина ();

4) ККД похилої площини (η = 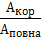∙ 100% = 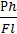∙ 100%)

2. Результати обчислень занесіть до таблиці

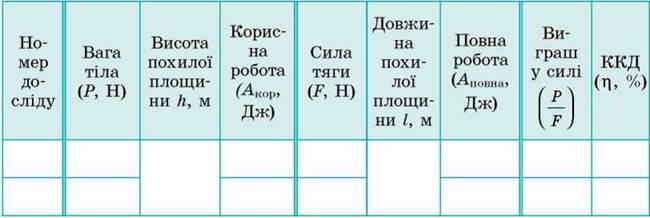
Аналіз експерименту та його результатів

1) Для кожного досліду порівняйте значення сили (F) зі значенням ваги тіла (P) і зробіть висновок про виграш у силі, який дає похила площина.

2) Порівняйте одержані значення ККД і зробіть висновок, чи залежить ККД від ваги тіла, яке піднімають похилою площиною.

Творче завдання

З’ясуйте за допомогою експерименту, як залежить ККД похилої площини від кута її нахилу. Чому, на вашу думку, змінюється ККД в разі зміни кута нахилу площини?

ПІДБИВАЄМО ПІДСУМКИ РОЗДІЛУ 4

“Механічна робота та енергія”

1. У розділі 4 ви дізналися про механічну роботу, механічну енергію і потужність.

Механічна робота, Дж	Енергія, Дж	Потужність, Вт
A = Fl [А] = Дж 1 Дж = 1Н 1м Характеризує рух тіла, до якого прикладено силу	[Е] = Дж Характеризує здатність тіла (або системи тіл) виконувати роботу	N = [N] = Вт; 1Вт = Характеризує швидкість виконання роботи

2. Ви навчилися розрізняти кінетичну і потенціальну енергії та дізналися про повну механічну енергію.

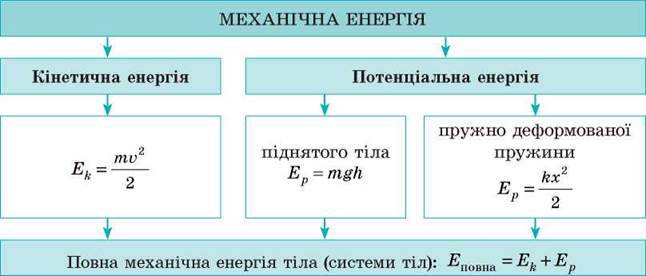
3. Ви ознайомились із законом збереження і перетворення механічної енергії та дізнались, як змінюється механічна енергія, якщо існує тертя:

За умови відсутності тертя виконується закон збереження і перетворення механічної енергії: Ek0+ Ер0 = Ek+ Ep

Якщо в системі існує тертя, то повна механічна енергія системи зменшується: Eповна0 > Eповна

4. Ви ознайомилися з простими механізмами.

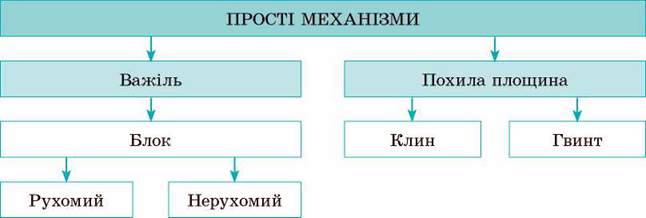
5. Ви з’ясували, що жоден простий механізм не дає виграшу в роботі, та ознайомилися з фізичною величиною – коефіцієнтом корисної дії механізму.

η = 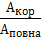∙ 100%

Використання простих механізмів для підйому тіл

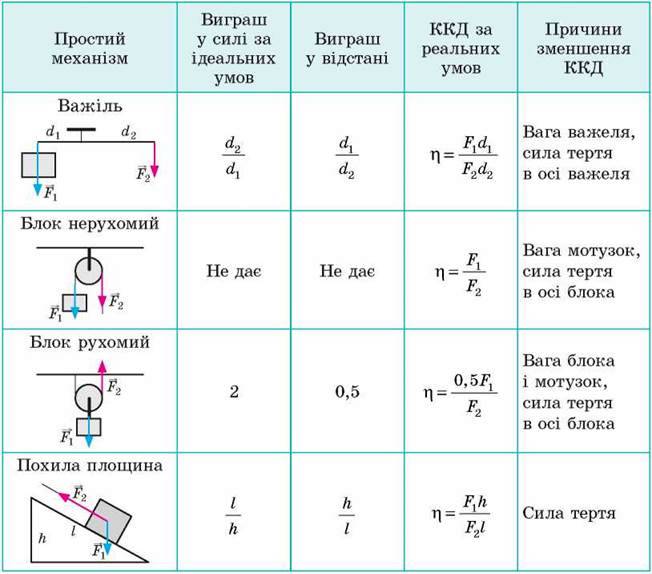
ЗАВДАННЯ ДЛЯ САМОПЕРЕВІРКИ ДО РОЗДІЛУ 4

“Механічна робота та енергія”

У завданнях 1-9 виберіть одну правильну відповідь.

Вважайте, що g = 10 Н/кг.

1. (1 бал) За відомими силою тяги літака та шляхом, який подолав літак у напрямку дії цієї сили, можна визначити:

А) швидкість руху літака;

Б) потужність, яку розвиває сила тяги літака;

В) роботу сили тяги літака;

Г) час руху літака.

2. (1 бал) Автомобіль рухається горизонтальною ділянкою дороги з певною швидкістю. Зі збільшенням швидкості руху автомобіля в 2 рази:

А) кінетична енергія автомобіля збільшується в 4 рази;

Б) потенціальна енергія автомобіля збільшується в 4 рази;

В) ККД двигуна автомобіля збільшується в 2 рази;

Г) кінетична енергія автомобіля збільшується в 2 рази.

3. (1 бал) Якщо потужність механізму дорівнює 100 Вт, то цей механізм:

А) за 100 с виконує роботу 1 Дж; в) за 1 с виконує роботу 0,01 Дж;

Б) за 10 с виконує роботу 10 Дж; г) за 1 с виконує роботу 100 Дж.

4. (1 бал) Рухомий блок застосовують:

А) для виграшу в силі або у відстані; в) для виграшу в роботі;

Б) лише для виграшу в силі; г) для зміни напрямку сили.

5. (1 бал) Якщо використання простого механізму дає виграш у силі в 6 разів, то за ідеальних умов він дає:

А) програш у відстані в 6 разів; в) програш у відстані в 36 разів;

Б) виграш у відстані в 6 разів; г) виграш у відстані в 36 разів.

6. (2 бали) Яку роботу треба виконати, щоб витягти відро з водою із колодязя завглибшки 12 м? Маса відра з водою дорівнює 8 кг.

А) 1,5 Дж; б) 15 Дж; в) 96 Дж; г) 960 Дж.

7. (2 бали) Якою є потужність двигуна, якщо за 4 хв він виконує роботу 12 кДж?

А) 50 Вт; б) 500 Вт; в) 3 кВт; г) 12 кВт.

8. (2 бали) Кран підняв вантаж вагою 24 кН, виконавши при цьому роботу 360 кДж. На яку висоту було піднято вантаж?

А) 15 см; б) 1,5 м; в) 15 м; г) 21,6 м.

9. (2 бали) За який час двигун потужністю 100 Вт виконає роботу 2 кДж?

А) 0,05 с; б) 20 с; в) 50 с; г) 200 с.

10. (З бали) Кит, плаваючи під водою зі швидкістю 18 км/год, розвиває потужність 150 кВт. Визначте силу опору води.

11. (3 бали) Загальна маса двох вантажів (рис. 1) дорівнює 25 кг. Якою є маса кожного вантажу, якщо важіль перебуває в рівновазі?

12. (3 бали) Яку силу треба прикласти до вільного кінця шнура (рис. 2), щоб рівномірно піднімати вантаж масою 12 кг? На яку висоту підніметься вантаж, якщо точка Aпереміститься на 20 см? Масою блоків і силою тертя знехтуйте.

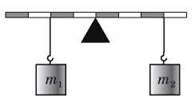
Рис. 1

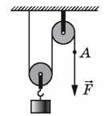
Рис. 2

13. (3 бали) За допомогою підйомника автомобіль масою 2 т підняли на висоту 2 м. Визначте виконану при цьому роботу, якщо ККД підйомника становить 80 %.

14. (3 бали) За допомогою нерухомого блока піднімають вантаж, прикладаючи силу 1,6 кН. Якою є маса вантажу, якщо ККД блока становить 80 %?

15. (4 бали) Довге плече важеля в 3 рази більше за коротке. Щоб підняти вантаж масою 60 кг, підвішений до короткого плеча важеля, до довгого плеча приклали силу 250 Н. Визначте ККД важеля.

16. (4 бали) ККД похилої площини становить 70 %. Щоб підняти вантаж масою 14 кг, необхідно прикласти силу 60 Н. Якою є довжина похилої площини, якщо її висота дорівнює 30 см?

17. (4 бали) За допомогою рухомого блока піднімають вантаж масою 40 кг, а вільний кінець мотузки тягнуть із силою 300 Н. Визначте ККД рухомого блока.

18. (4 бали) М’яч масою 0,5 кг підкидають вертикально вгору з початковою швидкістю 20 м/с. Знайдіть потенціальну і кінетичну енергії м’яча в той момент, коли швидкість його руху зменшиться в 2 рази. Опір повітря не враховуйте.

19. (4 бали) Тіло масою 5 кг розташоване на горизонтальній площині. Тіло почало рухатися в напрямку рівнодійної і, подолавши шлях 10 м, набуло швидкості руху 10 м/с. Визначте рівнодійну сил, що діють на тіло.

Звірте ваші відповіді на завдання з наведеними наприкінці підручника. Позначте завдання, які ви виконали правильно, і полічіть суму балів. Потім цю суму поділіть на три. Одержане число відповідатиме рівню ваших навчальних досягнень.

Тренувальні тестові завдання з комп’ютерною перевіркою ви знайдете на електронному освітньому ресурсі “Інтерактивне навчання”.

Навіщо свідомо знищувати автомобілі

Народна мудрість говорить: “Знав би, де впадеш, соломки підстелив би”. Здебільшого цей вираз використовують у переносному значенні, проте й буквальне його значення є правильним з точки зору фізики. “Соломка”, на яку м’якше падати, – це спортивні мати у фізкультурному залі, купа порожніх картонних ящиків для страхування каскадерів та інші прості засоби захисту людини від ушкоджень під час імовірного падіння. А як згадану народну мудрість використовують інженери?

Якщо тіло під час руху зіткнеться з перешкодою, то відбудеться деформація тіла та перешкоди. У випадку якщо таким тілом є, наприклад, морозиво, яке впало на підлогу, то, погодьтеся, лихо є невеликим. А от якщо автомобіль зіштовхнеться з іншим автомобілем або з бетонною огорожею, то це може стати трагедією.

Зрозуміло, що конструктори автомобілів не можуть повністю запобігти аварій, проте вони намагаються зробити так, щоб їх наслідки були якомога меншими.

Для цього автомобілі конструюють таким чином, щоб деформації зазнавала тільки його передня (задня) частина, а салон був якнайкраще захищений від зминання. Перевірку своїх ідей інженери здійснюють за допомогою так званих краш-тестів. Для проведення такого тесту абсолютно новий автомобіль оснащують величезною кількістю датчиків, у салоні розміщують манекени, які теж мають датчики. Після цього автомобіль розганяють до швидкості 40-60 км/год і спрямовують на перешкоду.

І зовсім не шкода свідомо знищувати новенький автомобіль, адже дані, отримані в результаті таких випробувань, дозволяють зберегти десятки людських життів. Обсяг даних, здобутих завдяки краш-тестам, є величезним.

На схемі наведено графік залежності кінетичної енергії автомобіля й енергії деформації від часу. Відлік часу починається в момент зіткнення автомобіля зі стіною. Уважні учні, напевно, помітять: якщо додати значення енергії деформації й кінетичної енергії за швидкості, скажімо, 40 м/с, то сума буде трохи меншою, ніж початкова кінетична енергія. Це пов’язане з тим, що вихідна кінетична енергія перетвориться й на інші види енергії, які не показані на графіку.

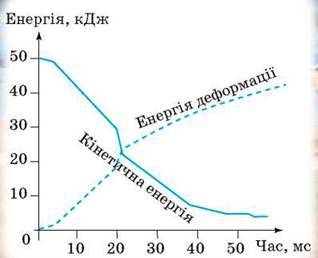
Результати краш-тесту: залежність кінетичної енергії (суцільна лінія) і енергії деформації (штрихова лінія) від часу випробовування.

Нуль на графіку позначає удар автомобіля об стіну

Теми рефератів і повідомлень

1. Важелі в живій природі.

2. Використання простих механізмів: історія і сучасність.

3. Прості механізми навколо нас.

4. Прості механізми в сучасних технічних приладах, обладнанні.

5. Історія відкриття закону збереження енергії.

6. Видатний український учений-механік С. П. Тимошенко.

7. Використання енергії води і вітру.

8. Потужність і габарити найпотужніших двигунів автомобілів, суден, літаків і ракет.

9. Важелі в нашому організмі.

10. Чи зміг би Архімед зрушити Землю?

11. Блоки та поліспасти на яхтах і вітрильниках.

12. Старовинні бойові катапульти.

Теми експериментальних досліджень

1 . Визначення потужності, яку розвивають школярі на уроках фізкультури.

2. Визначення ККД велосипеда під час нерівномірного руху.

3. Виготовлення поліспаста з підручних засобів і визначення його ККД.

4. Виготовлення пристрою, який працює на енергії падіння води. Оцінювання його ККД.

5. Визначення силових характеристик м’язів плеча під час підйому важкого портфеля.

6. Вимірювання потужності струменя води, що тече з крану під час умивання.