РІВНОМІРНИЙ РУХ ПО КОЛУ
Розділ ІІ Механічний рух
& 16. РІВНОМІРНИЙ РУХ ПО КОЛУ
Обертаються навколо осі: стрілки годинника (мал. 16.1), колеса велосипеда (мал. 16.3). Багато деталей машин та механізмів здійснюють обертальний рух, бо його дуже просто реалізувати.
Тіло може обертатися навколо осі, яка лежить поза його межами або навколо кількох осей: наприклад, кабіни колеса огляду (мал. 16.2). Наша планета Земля обертається навколо власної осі і навколо Сонця.
Період обертання
Розглянемо рівномірне обертання тіла, коли кожен оберт здійснюється за один і
Т = 
. (16.1)
Кожна точка тіла, що обертається навколо нерухомої осі, описує коло
Довжина траєкторії, що її проходить точка за один оберт, – це довжина
позначають грецькою літерою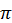 
(читається “пі”): 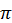= ≈ 3,14. (16.2)
Мал. 16.1.
Мал. 16.2.
Мал. 16.3.
Виходячи з визначення числа п, можна записати формулу для обчислення довжини кола, описаного точкою:
L = 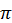d. (16.3)
Оскільки d = 2r, то довжину кола можна виразити через радіус:
L = 2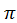
r (16.4)
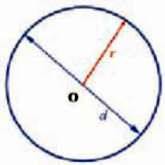
Мал. 16.4.
Швидкість матеріальної точки під час руху по колу
Швидкість матеріальної точки при рівномірному русі по колу (її ще називають лінійною швидкістю) можна обчислити, якщо поділити
Шлях, пройдений точкою за період (довжину кола) на відповідний час руху (період):
V =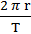 
(16.5)
Приклад 16.1
Визначте лінійну швидкість точок екватора при обертанні землі навколо своєї осі. Радіус земної кулі R = 6 400 км, період обертання 24 год.
Розв’язання. За формулою v = 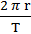, підставивши в неї числові значення, отримаємо: v = 
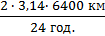= 1675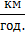 
Відповідь. Швидкість руху точок екватора становить 1675 .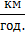
Зазначимо, що це удвічі більше, ніж швидкість авіалайнера.
Частота обертання
Кількість обертів за одиницю часу називають частотою обертання і позначають літерою “n”. Найчастіше частоту обертання вимірюють в обертах за секунду або обертах за хвилину. Якщо за час t тіло зробило N обертів, то частота дорівнює:
N = 
. (16.6)
Порівнявши формули (16.1) і (16.6), бачимо, що частота й період – взаємно обернені величини:
Т = 
, n = 
. (16.7)
Приклад 16.2
За 5 с колесо велосипеда радіусом 50 см зробило 20 обертів. Чому дорівнюють його: а) період обертання; б) частота обертання; в) швидкість точок обода?
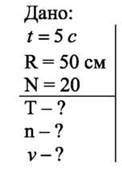
Розв’язання, а) Згідно з формулою Т = , Т= 5 с : 20 = 0,25 с.
Б) Формула n = дає: n = 20 : 5с = 4 
.
Читають: 4 оберти за секунду. Слово “оберти” у формулах не пишуть – треба здогадуватися самому.
В) Використовуючи разом формули v =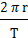 
та = n, отримуємо:
V = 2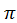 R ∙ n = 2 ∙ 3,14 ∙ 0,5м ∙ 4 = 12,56 
≈ 12,6 .
Відповідь, а) Т = 0,25 с; n = 4 (); v = 12,56 
≈ 12,6 .
Цікаво знати. Вал автомобільного двигуна може обертатися з частотою 500 -5000 обертів за хвилину, залежно від того, як сильно водій тисне на педаль акселератора (педаль “газу”). В автомобілі є прилад, що вимірює частоту – тахометр.
Вал турбіни реактивного двигуна робить 30 000 обертів за хвилину, центрифуга пральної машини – декілька сот обертів за хвилину, а ультрацентрифуга в біологічних лабораторіях – до півмільйона обертів за хвилину.
Коло та еліпс
Коло – це плоска замкнена крива, усі точки якої рівновіддалені від деякої заданої точки, що називається центром кола. Відстань від будь-якої точки кола до центру називають радіусом кола r. Відрізок, що сполучає дві точки на колі й проходить через його центр, називається діаметром d. Коло можна намалювати циркулем.
Дослід 16.1
Інший спосіб намалювати коло полягає в тому, що ви, увіткнувши у плоску поверхню шпильку, накидаєте на неї петлю (мал. 16.5) і, натягуючи її загостреним кінчиком олівця, проводите ним по поверхні, отримуючи коло. Центр кола можна назвати його фокусом, а коло можна назватиоднофокусною фігурою (мал. 16.5).
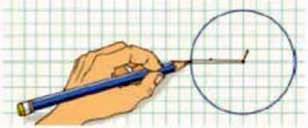
Мал. 16.5. Коло можна розглядати як однофокусну криву
З історії науки.
Чи можна у шкільному віці зробити відкриття?
Мова йтиме про англійського фізика Джеймса Кларка Максвела, який 150 років тому відкрив радіохвилі.
Милуючись якось в музеї формою овальних ваз, що збереглися від древніх етрусків, чотирнадцятилітній Максвелл замислився над тим, чи не можна намалювати еліпс так само просто, як і коло. І ось що він придумав. Якщо, як у досліді 16.1, петлю накинути на дві голки, увіткнуті в папір на деякій відстані одна від одної, а довжину нитки зробити трохи більшою, ніж подвоєна відстань між голками, і, натягуючи кінцем олівця нитку провести замкнену криву, то отримаємо двофокусну фігуру – еліпс (мал. 16.6). Точки, де знаходяться голки (F1 та F2), і є фокусами еліпса. Сума відстаней r1+r2 від довільної точки еліпса до фокусів однакова для всіх точок даного еліпса.
Еліпс має дві взаємно перпендикулярні осі – малу і велику. Точка О – центр еліпса – лежить на перетині його осей. Велика вісь еліпса проходить через обидва фокуси, а відрізок ОВ (або ОА) називають великою піввіссю еліпса. Орбіти планет, супутників планет та більшості штучних супутників Землі – еліпси.
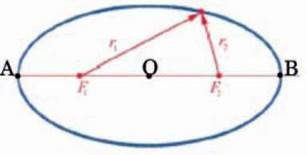
Мал. 16.6. Еліпс
Підведемо підсумки
Час, за який тіло здійснює один оберт, називають періодом оберттання: Т = .
– Кількість обертів за одиницю часу називають частотою обертання: n = .
– Частота й період – взаємно обернені величини: Т = , n = .
– Швидкість матеріальної точки при рівномірному русі по колу обчислюється за формулою: v = .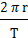
Тема для дослідження
16.1. Як на досліді визначити частоту обертання дзиги (мал. 16.7)?
16.2. Чому дзига не падає, коли крутиться?
Мал. 16.7. Чому дзига не падає, коли крутиться?
Вправа 16
1. Що називають: а) періодом обертання, б) частотою обертання, в) рівномірним обертанням?
2. Від чого залежить швидкість обертання матеріальної точки?
3. Як називають прилад, що вимірює частоту обертання?
4. Назвіть властивості кола.
5. Наведіть два способи побудови кола.
6. Чому дорівнює відношення довжини кола до його радіуса?
7. Як можна обчислити частоту обертання, знаючи період?
8. Знайдіть довжину екватора Землі, якщо її радіус становить 6400 км.
9. Довжина кола дорівнює 62,8 см. Який радіус кола?
10. Вал двигуна робить 2400 обертів за хвилину, а) Яка частота (в обертах за хвилину) обертання вала? б) Яка швидкість точки (в м/с), віддаленої від осі обертання на 20 см?
11. Штучний супутник Землі рухається по коловій орбіті на відстані 600 км від поверхні планети зі швидкістю 7,9 км/с. Який період (у хв) обертання супутника?
12. Мотоцикліст рухається по колу радіусом 50 м зі швидкістю 90 км/год. За який час він проходить один круг?
13. Хлопчик обертає каштан на нитці довжиною 50 см, роблячи 2 оберти за секунду, а) Який період обертання каштана? б) Яку швидкість має каштан?
14. Чому дорівнює період обертання годинної стрілки годинника?
15. За якої умови еліпс перетвориться на коло?
16. Паралелі на глобусі є колами (мал. 16.8). Де знаходяться центри цих кіл і в яких межах змінюється їх радіус?
17. Паралелі й меридіани є колами. Чим вони різняться між собою?
Мал. 16.8.
Мал. 16.9.
Мал. 16 .10
18. Маленьке зубчате коліщатко обертається за годинниковою стрілкою з частотою 10 обертів за секунду (мал. 16.9). а) У який бік і з якою частотою обертається велике коліщатко? б) Який період обертання коліщаток?
19. Крайнє ліве коліщатко (мал. 16.10) обертається за годинниковою стрілкою. а) У який бік обертається крайнє праве коліщатко? б) Порівняйте частоту обертання крайніх коліщаток.
20. Допустимо, що Земля є ідеальною кулею, радіус якої 6400 км. Охопимо екватор нерозтяжною ниткою так, щоб вона прилягала до поверхні в усіх точках. Відтак збільшимо довжину нитки на 1 м. Між ниткою й екватором утвориться проміжок. Припустимо, що він скрізь буде однаковий. а) Чи зможе в нього проскочити миша? б) Яким буде результат, якщо ми повторимо такий самий дослід із м’ячем?
21. Ведуча зубчата передача велосипеда (мал. 16.11), яка зв’язана з педалями, утричі більша за зубчатку, зв’язану з колесом. Радіус колеса 40 см, а спортсмен робить один оберт педалями за одну секунду, а) Яка частота обертання ведучого колеса? б) З якою швидкістю (в км/год) рухається велосипедист?
22. Накресліть еліпс із півосями 6 і 4 см.
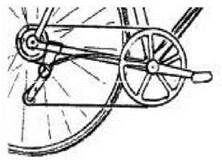
Мал. 16.11.
(1 votes, average: 5.00 out of 5)
Loading...