Розділ 3. Многочлени
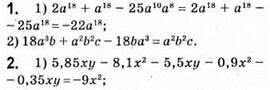
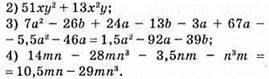
3. 1) 7×2 + х + 3; степінь 2;
2) -2х2 + 67x – 4,5; степінь 2;
3) 1,8х5 + 6х3 + 3х2 + 4х – 2,9; степінь 5;
4) 1/3×5 – 9,8х4 + 5×3 – 0,7×2 – 6; степінь 5;
5) 9,7а2b2 + 2b3а + баb + 3,75а; степінь 4;
6) 6,05b23а25 – а22b8 + 2b15а3 + 3; степінь 48.
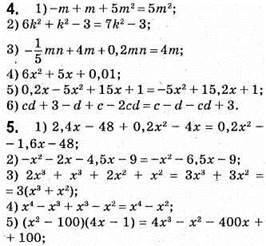
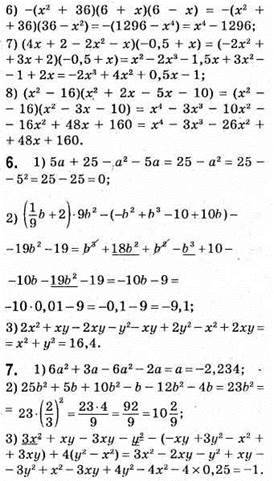
8.
Многочлен | Х – 6 | А + 1 | 0,3 + m2 | А2bс2 – аbс2 |
Многочлен | Х + 4 | А2 – а + 1 | M – 0,3 | -c2ab |
Сума | 2х – 2 | А2 + 2 | M2 + m | -2аbс2 |
Різниця | -10 | 2а – а2 | M2 – m + 0,6 | 2а2bс2 |
Добуток | Х2 – 2х – 24 | А3 + 1 | M3- 0,3m2+ 0,3m – 0,09 | А2b2с4 – а4b2с4 |
9.
Многочлен | -х3 – у2 | -х2 + 2х – 1 | У3 – 8у2 + 5 | А2 – 2 |
Многочлен | 6×3 + 4y2 – 4 | Х3 – х | -7у2 + 5 | A2 + 2 |
Сума | 5х3 + 3y2 – 4 | X3 – x2 + х – 1 | У3 – | 2а2 |
Різниця | -7×3 – 5y2 + 4 | -х3- x2 + 3x – 1 | -у2 + у3 | -4 |
Добуток | -6х6 – 10x3y2 – 4y4 + 4х3 + 4y2 | -x5 + 2х4 – 2х2 + x | -7y5 + 56y4 – 75y2 + 25 | А4 – 4 |
10. 1) 1,8а2 + 5,6b2 + 2,09а2 – 3b2 – 3,5а2 – 1 – 1 – 0,1b2 – 5а2 + 3,1b2 + 2 = -4,61а2 + 5,6b2; степінь 2;
2) -24а2 + 0,5b2 + 6 – 8а2 + 5b2 – 18а2 + 12 – 1,5b2 = -50а2 + 4b2 + 18; степінь 2;
3) а5 – 2а5 + а5 = 0; степінь 0;
4) х4n + х10n – х10n + х7n – x4n = х7n; степінь 7/7.
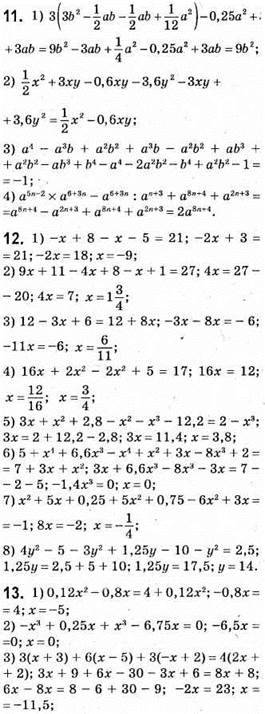
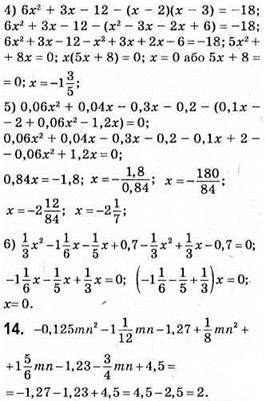
15. Нехай це числа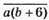 
і 
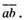
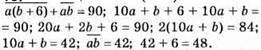
Числа 42 і 48.
16. 
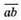– шукане число, тоді повинно виконуватися: 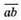= a + b + 18; 10a + b = a + b + 18; 9a = 18; a = 2; b = a – 2 = 0.
Шукане число 20.
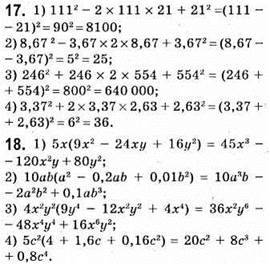
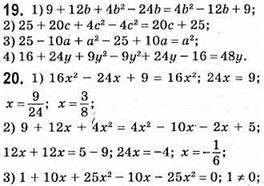
Немає розв’язку;
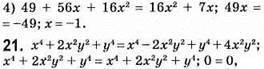
Що й потрібно було довести.
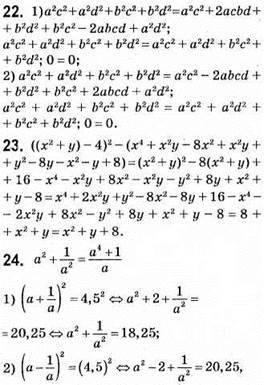
Маємо: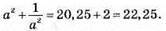 
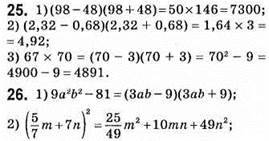
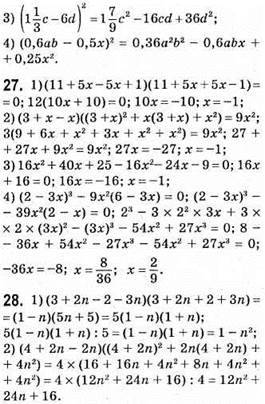
Тобто вираз ділиться на 4, що й потрібно було довести.
29. 1) 1 спосіб: Застосуємо формулу різниці квадратів:
(х + 3)2 – (х – 3)2 = (х + 3 + х – 3)(х + 3 – х + 3) = 2 • 6 = 12х;
2 спосіб: застосуємо формули “квадрат різниці” і “квадрат суми”:
(х + 3)2 – (х – 3)2 = х2 + 6х + 9 – х2 + 6х – 9 = 12х;
2) 1 спосіб: застосуємо формулу “різниця кубів”:
(х + 2)3 – (х – 2)3 = (х + 2 – х + 2)((х + 2)2 + (х + 2)(х – 2) + (х – 2)2) = 4(х2 + 4х + 4 + х2 – 4 + х2 – 4х + 4) = 4(3х2 + 4) = 12х2 + 16;
2 спосіб: (х + 2)(х + 2)(х + 2) – (х – 2)(х – 2)(х – 2) = (х2 + 4х + 4)(х + 2) – (х2 – 4х + 4)(х – 2) = х3 + 2х2 + 4х2 + 8х + 4х + 8 – (х3 – 2х2 – 4х2 + 8х + 4х – 8) = х3 + 6х2 + 12х + 8 – х3 + 6х2 – 12х + 8 = 12х2 + 16.
30. 1) Нехай n, n + 1 – два послідовних натуральних числа, тоді:
(n + 1)2 – n2 = (n + 1 – n)(n + 1 + n) = 2n + 1 – непарне число при будь-яких n.
2) 2k і 2k + 2 – два парних послідовних натуральних числа.
(2k + 2)2- (2k)2 = (2k + 2 + 2k)(2k + 2 – 2k) = 2(4k + 2) = 2 • 2 • (2k + 1) = 4(2k + 1);
4(2k + 1) : 4 = 2k + 1, що й треба було довести.
3) 2k + 1 і 2k + 3 – непарні послідовні натуральні числа.
(2k + 3)2 – (2k + 1)2(2k + 3 – 2k – 1)(2k + 3 + 2k + 1) = 2(4k + 4) = 2 • 4(k + 1) = 8(k + 1);
8(k + 1) : 8 = k + 1, що й треба було довести.
31. Нехай сторона квадрата х см, тоді сторони прямокутника (х – 3) см та (х + 4) см, звідси:
X2 = (х – 3)(х + 4); х2= x2 + 4х – 3х – 12; х = 12.
12 см – сторона квадрата; 9 смі 16 см – сторони прямокутника.
32. Нехай початкова сторона квадрата дорівнює х см, тоді (х – 3) см – сторона квадрата після зменшення. Складаємо рівняння:
Х2 – (х – 3)2 = 39; х2- х2 + 6х – 9 = 39; 6х = 48; х = 8.
Початкова сторона квадрата – 8 см.
33. Нехай початкова сторона куба х см, тоді (х – 2) см – сторона після зменшення. Складаємо рівняння:
Х3 – (х – 2)3 = 218; (х – х + 2)(х2 + х(х – 2) + (х – 2)2) = 218; 2(х2 + х2 – 2х + х2 – 4х + 4) = 218; 3х2 – 6х + 4 = 109; 3×2 – 6х – 105 = 0; x2 – 2х – 35 = 0; х = 7 – підходить.
7 см – початкова сторона куба.
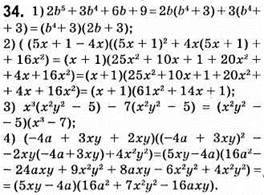
35. n, n + 1, n + 2 – три послідовні натуральні числа.
N • (n + 2) = (n + 1)2 – 1; n2 + 2n = n2 + 2n + 1 – 1; n2 + 2n = n2 + 2n; 0 = 0. Що й треба було довести.
(1 votes, average: 5.00 out of 5)
Loading...