Розкриття дужок
Урок № 77
Тема. Розкриття дужок
Мета: відпрацювати навички застосування вивчених правил для розв’язування завдань, що передбачають як розкриття дужок, так і заключення кількох доданків у дужки; вдосконалювати вміння обчислювати значення та спрощувати алгебраїчні суми.
Тип уроку: застосування знань, умінь і навичок.
Хід уроку
І. Перевірка домашнього завдання
@ Ретельно перевіряємо вправи на використання правил розкриття дужок.
Щоб охопити роботою якомога більше учнів, можна запропонувати їм завдання, складене
Наприклад. Розкрийте дужки і знайдіть значення виразу:
1. -32 – (53 – 72) = … 32 … 53 … 72 = …
2. -12+ (-32- 17) = … 12… 32… 17 = …
І т. ін.
Після того, як зберемо аркуші з відповідями, перевіряємо виконання, назвавши, які саме номери були запропоновані. Розбираємо помилки.
II. Актуалізація опорних знань
Усні вправи
1. Обчисліть:
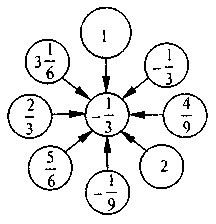
2. Який з поданих виразів дістанемо, розкривши дужки -(-a – b) + (-b)?
А) – а; б) а + b; в) а; г) а – 2b.
3. Замість… поставте відповідно знак “+” або “-“,
A) … a… (b + c) = – a + b + c;
Б) … a… (-b + c) = a – b + c;
В) … a… (-b + c) = – a + b – c.
4. Назвіть яке-небудь число, яке
А) менше від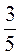 
, але більше за 
;
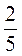Б) менше від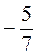 
, але більше за 
;
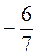В) менше від 0,17, але більше за – 0,16.
III. Доповнення знань
Розбираємо, як заключити доданки даної суми в дужки, перед якими стоїть знак “+” або “-“. Зважаємо на те, що правило, вивчене на попередньому уроці, працює як у “прямому” (тобто для розкриття дужок), так і в “зворотному” напрямку (тобто під час заключення доданків даної алгебраїчної суми в дужки, перед якими стоїть знак “+” або “-“).
IV. Відпрацювання навичок
1. Розкрийте дужки і знайдіть значення виразу:
А)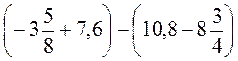 
;
Б)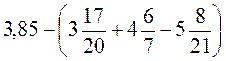 
;
В)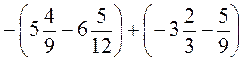 
;
Г)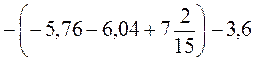 
;
Д)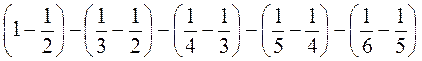 
.
2. Запишіть суму виразів і спростіть її:
А) -5 + а і – а + 2,3;
Б) 0,35 + m і -4,4 – m – 2,65;
В) a – b i b – a;
Г) a – b + с і b – а +3.
Запишіть різницю виразів і спростіть її:
А) с + 17,1 і 8,5 + с;
Б) – a+b і b – a;
В) а + b i b + с;
Г) – a + b + k i b – a – 2.
@ Дуже важливо саме на цих вправах пояснити, що, на відміну від запису суми або різниці двох чисел (коли ми просто ставимо між числами відповідний знак), для запису суми чи різниці виразів ми повинні спочатку заключити вирази в дужки, а потім вже ставити між ними відповідний знак (“+” або “-“).
3. Розв’яжіть рівняння, спростивши спочатку вираз у лівій частині:
а) 4,8 – (5,8 + х) = 1,2;
Б) (х + 7,2) – 14 = 2,3;
В) -9+(14,7 – x) = 1,3;
г) – (x – 1,9) – 15 = 14,1.
4. Візьміть у дужки два останні доданки, поставивши перед дужками знак “+”; знак “-“:
А) – 4 + 3 – 7; б) b – а +5; в) 8 – a + b; г) 5 – а – b.
5. У парку росте 450 дерев. Липи становлять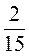 
кількості всіх дерев і 80 % кількості осик. Скільки лип і осик разом росте в парку?
V. Підсумки уроку
Тестові завдання
1. Який вираз дістанемо, розкривши дужки -(а – b) + (-р)?
1) – a + b – p; 2) a – b + p; 3) – a – b – p; 4) – a + b + p.
2. Спростіть вираз (р – 2) – (р – k + 4) + (1 – р).
1) – p + k – 5; 2) – р – k + 3; 3) 3р + k + 7; 4) -3р – k +3.
3. Знайдіть різницю виразів х – у + 2 та у + х – 4.
1) 2x – 2; 2) -2у + 6; 3) 2у + 6; 4) 2х – 2у – 2.
4. Знайдіть розв’язок рівняння 32 – (3 – х) = 21 – 32.
1) 46; 2) -40; 3) -18; 4) 23.
VI. Домашнє завдання
1. Спростіть вираз a – b + (b – c) + 1,8 і знайдіть його значення, якщо а = 0,2; b = -0,35; с = -3.
2. Розкрийте дужки і знайдіть значення виразу:
А)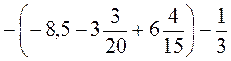 
; б)
.
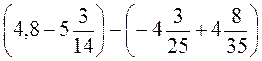3. Розв’яжіть рівняння, спростивши спочатку вираз у лівій частині: а) 8,3 – (-3,2 + х) = 12; б) -(х – 2,25) + 4,88 = 1,3.
4. Візьміть у дужки два останні доданки, поставивши перед дужками знак “+”; знак “-“:
А) 5 + 8 – 3; б) 7 – а + b; в) а – 5 + b; г) -4+ а + b.
(1 votes, average: 5.00 out of 5)
Loading...