Рух тіла під дією кількох сил
1-й семестр
МЕХАНІКА
2. Динаміка
Урок 17/37
Тема. Рух тіла під дією кількох сил
Мета уроку: ознайомити учнів з алгоритмом розв’язування задач на рух тіла під дією кількох сил
Тип уроку: закріплення знань
РЕКОМЕНДАЦІЇ ЩОДО ПРОВЕДЕННЯ УРОКУ
На попередніх уроках було розглянуто основні питання динаміки: вивчено три закони Ньютона, уведено основні поняття (маса, сила), з’ясовано особливості сил природи, що проявляють себе в механіці, показано розв’язування основної задачі механіки.
На цьому уроці висувається
Алгоритм розв’язування задач з динаміки
1. Уважно прочитайте умову задачі. З’ясуйте, які сили діють на тіло та характер руху тіла (рухається тіло прямолінійно й рівномірно чи з прискоренням).
2. Запишіть коротко умову задачі, виразіть числові значення СІ.
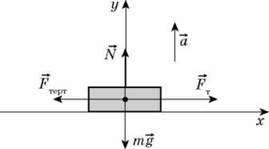
3. Зробіть схематичний рисунок, покажіть на ньому всі сили, що діють на тіло, і напрям прискорення.
4. Запишіть другий закон Ньютона у векторному вигляді та проекціях на осі
5. Запишіть додаткові рівняння (наприклад, формули для сил або рівняння кінематики).
6. Розв’яжіть отриману систему рівнянь у загальному вигляді.
7. Проаналізуйте отриманий результат (перевірте одиниці величин, розгляньте окремі або граничні випадки).
8. Виконайте числові розрахунки, оцініть правдоподібність результатів.
9. Запишіть відповідь.
Задачі для розв’язування на уроці
1. Собача запряжка починає тягти санки масою 100 кг, що стоять на снігові, з постійною силою 150 Н. За який проміжок часу санки проїдуть перші 200 м шляху? Уважайте, що коефіцієнт тертя ковзання полоззя об сніг дорівнює 0,05.
Розв’язок
Щоб обчислити час руху санок, необхідно знати прискорення, з яким рухаються санки, і початкову швидкість. Оскільки санки рушають з місця, то їхня початкова швидкість дорівнює нулю. Прискорення обчислимо, скориставшись другим законом Ньютона.
На санки діють чотири сили: сила тяжіння m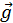
, сила реакції опори 
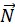, сила тяги собак 
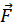T і сила тертя ковзання 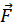Терт. ковз.
Запишемо другий закон Ньютона:
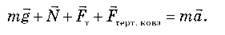
Спроектуємо рівняння на осі координат і запишемо вираз для сили тертя:
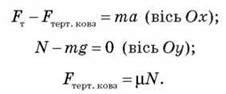
Ми отримали систему трьох рівнянь з трьома невідомими. Розв’язавши цю систему, ми й дістанемо прискорення:
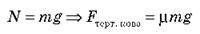
Підставивши отриманий вираз у перше рівняння, дістаємо: FT – ?mg = mа, звідки:
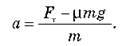
Для обчислення часу руху скористаємося рівнянням проекції переміщення для рівноприскореного руху:
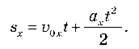
У нашому випадку:
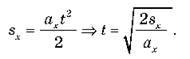
Підставляючи сюди значення прискорення, дістаємо:
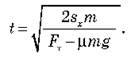
Перевіряємо одиниці величин:
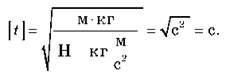
Виконуємо обчислення:
(Відповідь: санки проїдуть перші 200 м за 20 с).
2. Автомобіль масою 4 т рухається нагору, уповільнюючи свій рух. Обчисліть силу тяги, якщо ухил становить 0,02, а коефіцієнт опору руху дорівнює 0,04. Прискорення автомобіля постійне й дорівнює 0,15 м/с2.
Розв’язок
Термін “ухил” – це синус кута нахилу полотна дороги до горизонту. Якщо ухил малий (менше, ніж 0,1), то cos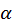
?1.
Коефіцієнт опору руху враховує всі види тертя (тертя кочення коліс об дорогу, тертя ковзання в осях автомобіля та ін.).
На автомобіль діють чотири сили: сила тяжіння m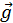, сила реакції опори 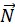,, сила тяги 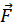T і сила опору 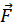Терт.
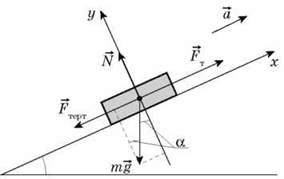
Запишемо другий закон Ньютона:
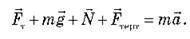
Спроектуємо рівняння на осі координат, з огляду на те, що mgx = – mgsin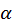; mgy = – mgcos.
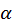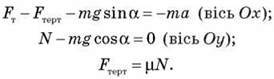
Ми отримали систему трьох рівнянь з трьома невідомими. Розв’язавши цю систему, ми дістанемо?:
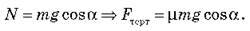
Підставляємо цей вираз у перше рівняння:
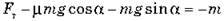
Звідки дістаємо:
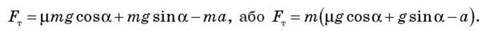
Перевіримо одиниці величин:
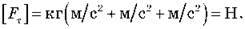
Виконаємо обчислення:
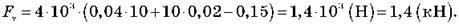
(Відповідь: сила тяги автомобіля – 1,4 кН)
3. На горизонтальній дорозі автомобіль робить поворот радіусом 45 м. Яку найбільшу швидкість може розвинути автомобіль, щоб його не занесло? Коефіцієнт тертя ковзання шин об асфальт дорівнює 0,5.
4. Кулька на нитці завдовжки 1 м рівномірно рухається по колу, при цьому нитка утворює з вертикаллю кут 45°. Обчисліть період обертання кульки.
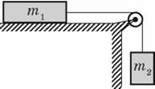
5. Тіло масою m1 = 1 кг ковзає по горизонтальній поверхні під дією важка масою m2 = 250 г (див. рис.). Система тіл рухається з прискоренням 1,5 м/с2. Обчисліть коефіцієнт тертя між тілом і поверхнею.
Домашнє завдання
1. П.: § 29.
2. 36.:
Р1) – 11.1; 11.4; 11.5; 11.6;
Р2) – 11.9; 11.12; 11.15; 11.20;
Р3) – 11.29; 11.30; 11.32; 11.33.
(1 votes, average: 5.00 out of 5)
Loading...