Головна ⇒ 📌Формули й таблиці ⇒ Степеневі функції з раціональними показниками – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ
Степеневі функції з раціональними показниками – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ
Формули й таблиці
МАТЕМАТИКА
ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ
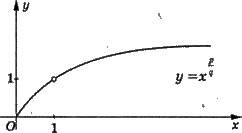
Степеневі функції з раціональними показниками
Related posts:
- Степеневі функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Степеневі функції Графіки функції є параболами степеня n Графіки функції є гіперболами Функція y = ах, де а > 0, а ≠ 1, називається показниковою функцією з основою а. Приклад 0 < а < 1 Y = (1/2)x А > 1 Y = 2х Область визначення Х […]...
- Лінійні функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Лінійні функції...
- Теорема Вієта – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Теорема Вієта Щоб числа x1 та х2 були розв’язками рівняння ах2 + bх + с = 0, необхідно й достатньо, щоб:...
- Квадратичні функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Квадратичні функції Графіком квадратичної функції є парабола, яка отримується з графіка функції у = ах2 за допомогою двох паралельних перенесень: – перенесення уздовж осі ОХ на m одиниць ліворуч, якщо m < 0, і праворуч, якщо m > 0; – перенесення уздовж осі OY на у0 одиниць […]...
- Обернені функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Обернені функції Дві функції називаються оберненими, якщо вони виражають ту саму залежність між змінними величинами, але в одній з них за аргумент прийнято х, а за функцію – у, в іншій – навпаки, тобто за аргумент прийнято у, а за функцію – х. Функції у = f(x) […]...
- Схема дослідження – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Функцією (або функціональною залежністю) називається закон, за яким кожному значенню незалежної змінної х з деякої множини чисел, що називається областю визначення функції, ставиться у відповідність тільки одне певне значення величини у. Графіком функції називається множина всіх точок координатної площини з координатами (х, у), такими, при яких абсциса […]...
- Функції та їхні властивості. Квадратична функція УРОК № 62 Тема. Функції та їхні властивості. Квадратична функція Тестові завдання 1. Знайдіть область визначення функції . А) х 5; Б) х -5; В) х -5, х 0; Г) х 3, х -5, х 0. 2. Знайдіть нулі функції . А) 0; 2; б) 2; в) 0; -2; г) нулів немає. 3. Яка з […]...
- Властивості тригонометричних функцій – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Властивості тригонометричних функцій Функції У = sin x У = cos x Y = tg x 1. Область визначення Х (-∞;+∞) Х (-∞;+∞) X ≠ π/2 + πn, n Z 2. Множина значень Y Y Y (-∞;+∞) 3. Періодичність Усі тригонометричні функції – періодичні з найменшим додатним періодом Т […]...
- Похідна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Похідна функція – визначення похідної функції. Рівняння дотичної до графіка функції y = f(x) у точці М(х0,у0): – кутовий коефіцієнт дотичної....
- Функції. Властивості функції: нулі функції, проміжки знакосталості, зростання і спадання функції УРОК № 19 Тема. Функції. Властивості функції: нулі функції, проміжки знакосталості, зростання і спадання функції Мета уроку: закріпити знання учнів про означення поняття нулів функції, проміжків знакосталості, функції, що зростає або спадає на проміжку, а також про способи відшукання названих характеристик функції у випадках, якщо функція задана графічно або аналітично. Закріпити вміння учнів виконувати дії […]...
- Формули приведення – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули приведення π/2 ± α π ± α 3 π/2 ± α 2π ± α 90° ± α 180° ± α 270° ± α 360° ± α Sin β Cosα Sinα -cosα ±sinα Cos β Sinα -cosα ±sinα Cosα Tg β Tgα ctgα Tgα Tgα ctgα ±tgα Ctg β […]...
- Первісна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Первісна функція Первісною для даної функції y = f(x) на проміжку (а; b) називається така функція F(x), похідна якої для всіх х (а;b), що дорівнює f(x): F'(x) = f(x). Загальний вигляд первісної F(x) + C, де С – довільне стале число. Теорема. Будь-яка неперервна на функція y = f(x) […]...
- Підсумковий урок з теми “Функції. Властивості функції. Функція у = ах2+bx+c. Розв’язування квадратних нерівностей” УРОК № 26 Тема. Підсумковий урок з теми “Функції. Властивості функції. Функція у = ах 2 + b х + С. Розв’язування квадратних нерівностей” Мета уроку: повторити, систематизувати й узагальнити знання та вміння учнів щодо змісту вивчених у розділі “Функція та її властивості” понять і схем розв’язування типових задач шляхом складання загальних алгоритмів розв’язування задач. […]...
- Властивості функцій – Функції та графіки Математика – Алгебра Функції та графіки Властивості функцій Функція називається Зростаючою на деякому проміжку, якщо більшому значенню аргументу із цього проміжку відповідає більше значення функції. Функція називається Спадною на деякому проміжку, якщо більшому значенню аргументу із цього проміжку відповідає менше значення функції. Якщо функція зростає (спадає) на всій області визначення, її називають зростаючою (спадною). Приклади […]...
- Формули перетворення сум у добутки – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули перетворення сум у добутки Для будь-яких α і β...
- Показникова функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Показникова функція У = ах (0 < а < 1) У = ах (а > 1) Область визначення Х (-∞;+∞) Х (-∞;+∞) Множина значень Y (0;+∞) Y (0;+∞) Перетин з віссю Y При х = 0, y = 1. При х = 0, y = 1. Монотонність Функція спадає […]...
- Тканини рослин: їхні функції та взаємозв’язок Розділ І. РОСЛИНИ Тема 1. Будова та життєдіяльність рослин (на прикладі покрито-насінної дводольної рослини) УРОК 6 Тема. Тканини рослин: їхні функції та взаємозв’язок Мета. Сформувати знання про основні типи тканин рослинного організму, вивчити функції, які вони виконують. Основні поняття і терміни: тканина; твірна (меристема), основна (паренхіма), провідна, покривна, механічна. Обладнання: підручник, робочі зошити, таблиці “Тканини […]...
- Обернені тригонометричні функції – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ У = sin x 0; π/2 π/2 π/2; π π π; 3π/2 3π/2 3π/2; 2π 2π M A X П E P E Т И Н И M I N П E P E Т И Н И У = cos x 0; π/2 π/2 π/2; π π π; […]...
- Формули перетворення добутків у суми – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули перетворення добутків у суми Для будь-яких α і β...
- Значення функцій деяких кутів – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Значення функцій деяких кутів α 0; 2π π/6 π/4 π/3 π/2 π 3π/2 0; 360° 30° 45° 60° 90° 180° 270° Sin α 0 1/2 /2 /2 1 0 -1 Cos α 1 /2 /2 1/2 0 -1 0 Tg α 0 1/ 1 Не існують 0 Не існують […]...
- Властивості сполучень – ЕЛЕМЕНТИ КОМБІНАТОРИКИ Формули й таблиці МАТЕМАТИКА ЕЛЕМЕНТИ КОМБІНАТОРИКИ Упорядкована множина з п елементів називається перестановкою: Рn = n! n! = n · (n – 1) · (n – 2) ·…· 3 · 2 · 1. Упорядкована підмножина з m елементів множини, що складається з n елементів (m ≤ n), називається розміщенням з n елементів по m. Довільна […]...
- ШТУЧНІ МАТЕРІАЛИ ТА ЇХНІ ВЛАСТИВОСТІ Робота із сучасними штучними матеріалами ШТУЧНІ МАТЕРІАЛИ ТА ЇХНІ ВЛАСТИВОСТІ Пластик (англ. plastic) – матеріал із пластмаси. Синтепон – синтетичний пухкий матеріал, здатний утримувати тепло; використовується для виготовлення ковдр, як підкладочний матеріал у швейних виробах. Поролон – легкий пористий еластичний матеріал, що утворюється з поліуретану і широко використовується, зокрема в побуті. 1. Які вироби із […]...
- Логарифмічна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Логарифмічна функція Y = logax(0 < a < 1) У = logax(а > 1) Область визначення Х (0;+∞) Х (0;+∞) Множина значень Y (-∞;+∞) Y (-∞;+∞) Перетин з осями координат З віссю ОХ Х = 1, у = 0; Х = 1, у = 0; З віссю OY Перетину […]...
- Органи рослин. їхні функції і взаємозв’язок. Корінь Розділ І. РОСЛИНИ Тема 1. Будова та життєдіяльність рослин (на прикладі покрито-насінної дводольної рослини) УРОК 7 Тема. Органи рослин. їхні функції і взаємозв’язок. Корінь Лабораторна робота № 2. Корінь і кореневі системи. Видозміни кореня Мета. Продовжити формувати в учнів знання, отримані з попередніх курсів, про органи рослин – вегетативні та генеративні; ознайомити з зовнішньою будовою […]...
- ТКАНИНИ. ТИПИ ТКАНИН І ЇХНІ ВЛАСТИВОСТІ – ОРГАНІЗМ ЛЮДИНИ І ЙОГО БУДОВА – ЛЮДИНА Біологія – універсальний довідник ЛЮДИНА ОРГАНІЗМ ЛЮДИНИ І ЙОГО БУДОВА ТКАНИНИ. ТИПИ ТКАНИН І ЇХНІ ВЛАСТИВОСТІ Тканина – це група клітин і міжклітинної речовини, які мають однакову загальну будову, функції і походження. В організмі людини розрізняють чотири основних типи тканин: епітеліальну (покривну), сполучну, м’язову і нервову. Епітеліальна тканина утворює шар клітин, з яких складаються покриви […]...
- Властивості степеня з цілим показником – СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Формули й таблиці МАТЕМАТИКА СТЕПЕНІ, КОРЕНІ, ЛОГАРИФМИ Степінь числа з натуральним показником n – добуток Позначуване аn; число а називається основою, а натуральне число n > 1 – показником степеня. Степінь числа з натуральним показником n називають n-м степенем числа а. Другий степінь числа називають квадратом цього числа. Степінь числа з нульовим показником – вираз […]...
- ОСНОВНІ ВЛАСТИВОСТІ ЛОГАРИФМІВ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ВЛАСТИВОСТІ ЛОГАРИФМІВ Для будь-якого додатного числа а, що не дорівнює 1: 1) loga1 = 0; 2) logaa = 1; 3) якщо х > 0 і у > 0, то logaху = logaх + logaу; 4) якщо х > 0 і у > 0, то logax/y = logax – logaу; 5) […]...
- Розв’язування вправ на всі дії з раціональними числами Уроки № 120, 121 Тема. Розв’язування вправ на всі дії з раціональними числами 1. Обчисліть: А) ; Б) ; В) ; Г) ; Д) ; Є) ; Ж) ; З) . 2. Виконайте дії: А) (66 – 78) : 0,12; Б) (-34,6 – 23,4) : (-5,8) – 10; В) ; Г) ; Д) ; Є) […]...
- Співвідношення між прямими й оберненими тригонометричними функціями – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Співвідношення між прямими й оберненими тригонометричними функціями...
- Основна тригонометрична тотожність – ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Формули й таблиці МАТЕМАТИКА ОСНОВНІ ФОРМУЛИ ТРИГОНОМЕТРІЇ Основна тригонометрична тотожність Для будь-якого x...
Чартизм »