СУМА І РІЗНИЦЯ КУБІВ
РОЗДІЛ 3 МНОГОЧЛЕНИ
&13. СУМА І РІЗНИЦЯ КУБІВ
Перелік формул скороченого множення, які ви знаєте, у цьому параграфі доповнимо ще двома формулами. Для цього спочаткy доведемо наступну теорему.
Запам’ятайте!
Теорема 1 (про добуток суми двох одночленів і неповного квадрата їх різниці).
Добуток суми двох одночленів і неповного квадрата їх різниці дорівнює сумі кубів цих одночленів:
(а + b)(а2 – аb + b2) = а + b3.
Д а н о: одночлени a i b.
Д о в е с т и: (a + b)(a2 – ab + b2) = a3 + b3.
Д о в е д е н н я. Перетворимо вираз у лівій частині
(а + b)(a2 – ab + b2) =
= а3 – a2b + ab2 + a2b – ab2+ b3 =
= а3 + b3.
Отже, а3 + b3 = а3 + b3.
Звідси (а + b)(a2 – ab + b2) = а3 + b3, що і вимагалося довести.
Теорема 2 (про добуток різниці двох одночленів і неповного квадрата їх суми).
Добуток різниці двох одночленів і неповного квадрата їх суми дорівнює різниці кубів цих одночленів:
(а – b) (а2 + ab + b2) = а3 – b3.
Д а н о: одночлени а і b.
Д о в е с т и: (a – b)(a2 + ab + b2) = a3 – b3.
Д о в е д е н н я. Перетворимо вираз у лівій частині цієї рівності так, щоб він набув вигляду виразу в її правій частині:
(a –
= а3 + a2b + ab2 – a2b – ab2 – b3 =
= a3 – b3.
Отже, a3 – b3 = a3 – b3.
Звідси (a – b)(a2 + ab + b2) = a3 – b3, що і вимагалося довести.
Загалом дістали:
(a + b)(a2 – ab + b2) = а3 + b3;
(а – b)(a2 + ab + b3) = а3 – b3.
Ці формули також є формулами скороченого множення. Вони дозволяють полегшувати перетворення виразів.
Оскільки доведені рівності є тотожностями, то їх можна застосовувати і в зворотному порядку:
А3 + b3 = (a + b) (a2 – ab + b2);
А3 – b3 = (а – b) (а2 + аb + b2).
Ці тотожності називаються відповідно формулою суми кубів і формулою різниці кубів.
? Чи можна застосовувати формулу суми (різниці) кубів не лише до найпростіших одночленів? Так.
Задача 1. Подайте у вигляді добутку двочлен 8 – x6y15.
Розв’язання. Число 8 є кубом числа 2. Другий член x6y15 даного двочлена можна подати як куб іншого одночлена: х6y15 = (х2y5)3. Звідси випливає, що до даного двочлена можна застосувати формулу різниці кубів:
8 – x6y15 =
= 23- (x2y5)3 =
= (2 – x2y5)(22+ 2х2y5 + (х2y5)2) =
= (2- х2у5) (4 + 2х2у5 + х4у10).
Зверніть увагу:
– сума кубів двох одночленів дорівнює добутку суми цих одночленів і неповного квадрата їх різниці;
– різниця кубів двох одночленів дорівнює добутку різниці цих одночленів і неповного квадрата їх суми;
– різниця квадратів двох одночленів дорівнює добутку суми і різниці цих одночленів.
Задача 2. Знайдіть значення виразу 253+ 125.
Розв’язання. Подамо другий доданок як степінь 53 та застосуємо відповідну формулу скороченого множення:
253+ 53 = (25 + 5) ∙ (252 – 25 ∙ 5 + 52) =
= 30 ∙ 25 ∙ (25 – 5 + 1) = 30 ∙ 25 ∙ 21 =
= 630 ∙ 100 : 4 = 15 750.
Отже, 253 + 125 = 15 750.
Зверніть увагу:
Формули суми кубів і різниці кубів можна застосовувати до будь-яких цілих виразів.
Дізнайтеся більше
Натуральні числа мають багато цікавих властивостей. Проте довести їх буває складніше, ніж виявити. Розглянемо приклад. Дільниками числа 6 є числа 1, 2, 3, 6. Для кожного із цих чисел визначимо кількість їх дільників. А саме: число 1 має один дільник, число 2 має два дільники, число 3 – два дільники, число 6 – чотири дільники. Отже, дістали набір чисел: 1, 2, 2, 4. Виявляється, що сума кубів цих чисел дорівнює квадрату їх суми, тобто: 13 + 23 + 23 + 43 = (1 + 2 + 2 + 4)2. Справді:
13 + 23 + 23 + 43 = 1 + 8 + 8 + 64 = 81;
(1 +2 + 2 + 4)2 = 92 = 81.
Щоб перевірити цю властивість ще раз, візьмемо число 16. Його дільники – 1, 2, 4, 8, 16. Знайшовши кількість дільників кожного із цих чисел, отримаємо набір чисел: 1, 2, 3, 4, 5. Складемо відповідні числові вирази:
13 + 23 + З3 + 43 + 53 = 1 + 8 + 27 + 64 + 125 = 225;
(1 + 2 + 3 + 4 + 5)2 = 152 = 225.
Отже, 13 + 23 + З3 + 43 + 53= (1 + 2 + 3 + 4 + 5)2.
Проте довести такий факт досить складно. Спробуйте. Можливо, ви зможете це зробити.
ПРИГАДАЙТЕ ГОЛОВНЕ
1. Сформулюйте і доведіть теорему про добуток суми двох одночленів і неповного квадрата їх різниці.
2. Запишіть формулу суми кубів.
3. Запишіть формулу різниці кубів.
4. Чому дорівнює сума кубів двох одночленів?
5. Чому дорівнює різниця кубів двох одночленів?
РОЗВ’ЯЖІТЬ ЗАДАЧІ
645. Укажіть правильне твердження:
1) добуток різниці двох одночленів і неповного квадрата їх різниці дорівнює сумі кубів цих одночленів;
2) добуток суми двох одночленів і повного квадрата їх різниці дорівнює сумі кубів цих одночленів;
3) добуток суми двох одночленів і неповного квадрата їх різниці дорівнює сумі кубів цих одночленів;
4) добуток суми двох одночленів і неповного квадрата їх суми дорівнює різниці кубів цих одночленів.
646. Чи правильно, що:
1) (а + b)(a2 + ab + b2) = а3 + b3; 3) (a + b)(a2 – ab + b2) = а3 + b3;
2) (а + b)(a2 – 2ab + b2) = а3 + b3; 4) (а – b)(a2 – ab + b2) = а3 + b3?
647. Чи правильно, що:
1) (а – b)(а2 + аb + b2) = а3 – b3; 3) (а – b)(а2- 2ab + b2) = а3 – b3;
2) (а + b)(а2 – аb + b2) = а3 – b3; 4) (а – b)(а2 – аb + b2).
648. Чи правильно, що:
1) а3 – b3 = (а + b)(а2 + аb + b2); З)а3 – b3 = (a – b)(a2 + 2ab + b2);
2) а3 – b3 = (а – b)(а2 + ab + b2); 4) а3 – b3 = (a + b)(а2 – аb + b2)?
649. Чи правильно, що:
1) а3 + b3 = (а + b)(а2 – аb + b2); 3) а3 + b3 = (а – b)(а2 – 2аb + b2);
2) а3 + b3 = (а – b)(a2 + аb + b2); 4) a3 + b3 = (а + b)(a2 + аb + b2)?
650 . Який із наступних виразів дорівнює добутку (х + у)(х2 – ху + у2):
1)x3 – y3; 2) х3 + у3; 3) х2 – у2; 4) у2 + х2?
651. Чи правильно, що (а + 2)(а2 – 2a + 4) дорівнює:
1)а2 + 4; 2)а3 + 4; 3)а3 – 8; 4)а3 + 8?
652. Чи правильно, що (t + 3)(t2 – 3t + 9) дорівнює:
1)t2 + 27; 2) t3 + 9; 3)t3 + 27; 4)t3 – 27?
653. Який із наступних виразів дорівнює виразу (2 + 3d )(4 – 6d + 9d2):
1) 23 + 3d3;
2) 23 – (3d)3;
3) 23 + (3d)3;
4) 22 – (2b)2?
654. Який із наступних виразів дорівнює добутку (m – n)(m2 + mn + n2):
1)n3 – m3;
2)m3 + n3;
3)m3 – n3;
4)m2 – n2?
655. Чи правильно, що (b – 5)(b2 + 5b + 25) дорівнює:
1) b2 – 25;
2) b3 + 125;
3) b3 – 125;
4) b3 – 25?
656. Який із наступних виразів дорівнює виразу (1 -5b)(1 + 5b + 25b2):
1) 1 + (5b)3;
2) 1 – (5b)3;
3) 1 – 5b3;
4) 1 – (5b)2?
657. Яка із наступних рівностей є тотожністю:
1) (х – 1)(х2 – х + 1) = х3 – 1; 3) (1 – х)(1 + х + х2) = 1 – х3;
2) (х – 1 )(х2 + х + 1) = х3 – 1; 4) (1 – х)( 1 – х + х2) = 1 – х3?
658. Який із наступних виразів дорівнює виразу (2 – t)(4 + 2t + t2):
1) 8 +13; 2) 8 – t3; 3) 4 + t3; 4)8 – t2?
659. Уставте замість зірочки такий одночлен, щоб утворилася тотожність:
1) (2а + 4b)(4а2 – 3аb + 16b2) = * + 64b3;
2) (5х – 3b)(25х2 + 15bх + 9b2) = 125х3 – *;
3) (-2х + 6у)(36у2 + 12ху + 4х2) = * – 8х3.
660. Подайте добуток у вигляді многочлена:
1) (b + c)(b2 – bc + с2); 5) (x – 3m)(x2 + 3mx + 9m2);
2) (а – х)(а2 + ах + х2); 6) (2b + 3d)(9d2 – 6bd + 4b2);
3) (m + t)(m2 – mt + t2); 7) (xy + 4)(x2y2 – 4xy + 16);
4) (с + 2d)(c2 – 2cd + 4d2); 8) (0,1a –  B)(0,01a2 +
B)(0,01a2 + 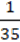 Ab +
Ab + 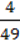 B2)
B2)
661. Подайте добуток у вигляді многочлена:
1) (а – n)(а2 + an + n2);
2) (b + 5d)(b2 – 5bd + 25d2);
3) (у – 4х)(у2 + 4ху + 16х2);
4) (5mn – 2а)(25m2n2 + 10аmn + 4а2).
662. Чи правильно, що а3 – 8 дорівнює:
1) а(а – 2)(а + 2); 3)(а – 2)(а2 + а + 4);
2) (a -2)3; 4) (а – 2)(а2 + 2а + 4)?
663. Чи правильно, що 1 – 27y 3 дорівнює:
1) (1 – 3у)(1 + 9у + 9у2); 3) (1 – 3у)(1 +3у + 9у2);
2) (1 – 3у)(1 – 3y + 9y2); 4) (1 – 3у)(1 + 6у + 9у2)?
664. Розв’яжіть рівняння:
1) (1 + х)(х2 – х +1) – х3 = х;
2) (2х + 1 )(4х2 – 2х + 1) – 8х3 + х = 2;
3) х3 – (х – 3)(х2 + 3х + 9) – 3х = 0.
665. Розв’яжіть рівняння:
1) (1 – х)( 1 + х + х2) + х3 – х = 0;
2) (3х + 1)(9х2 – 3х + 1) – 27х3 + 2х = 3.
666. Чи є тотожністю дана рівність:
1) 8с3 – 1 = (2с – 1 )(с2 – 2с +1); 3) 8с3 – 1 = (2с – 1 )(4с2 + 2с + 1);
2) 8с3 – 1 = (2с – 1 )(4с2 – 2с + 1); 4) 8с3 – 1 = (2с – 1 )(4с2 + 4с + 1)?
667. Чи правильно, що 113 + 93=…:
1) (11 +9)(112 + 92) = 20 ∙ (121 + 81) = 4040;
2) (11 + 9)(112 + 11 ∙ 9 + 92) = 20 ∙ (121 + 99 + 81) = 6020;
3) (11 + 9)(112 – 2 ∙ 11 ∙ 9 + 92) = 20 ∙ (121 – 198 + 81) = 80;
4) (11 + 9)(112 – 11 ∙ 9 + 92) = 20 ∙ (121 – 99 + 81) = 2060?
У неправильних рівностях укажіть, де допущено помилку.
668. Чи правильно, що 113 – 103=…:
1) (11 – 10)(112 + 102) = 1 (121 + 100) = 221;
2) (11 – 10)(112 + 11 ∙ 10 + 102) = 1 (121 + 110 + 100) = 331;
3) (11 – 10)(112 + 2 ∙ 11 ∙ 10 + 102) = 1 (121 + 220 + 100) = 441;
4) (11 – 10)(112 – 11 ∙ 10 + 102) = 1 (121 – 110 + 100) = 111?
У неправильних рівностях укажіть, де допущено помилку.
669. Використовуючи формули суми та різниці кубів, обчисліть:
1 )73 + З3; 2)93 – 83; 3) 1,13 + 0,93; 4)0,93 – 0,83.
670. Використовуючи формули суми та різниці кубів, обчисліть:
1) 73 – 63; 2) 0,43 + 0,63.
671. Якому із наступних виразів тотожно дорівнює двочлен 8x6y12 – 27:
1) (2 – 3)(4х6y8 + 6х3y6 + 9);
2) (2х2y4 – 3)(4х4y8 + 12x2y4 + 9);
3) (2х2y4 – 3)(4х4у8 + 6х2у + 9)?
672. Уставте замість зірочки такий одночлен, щоб утворилася тотожність:
1) 8a3b3 – 125 = (* – 5)(4а2b2 + 10ab + 25);
2) 0,216a6b9 – 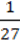 C12 = (0,6a2b3 –
C12 = (0,6a2b3 –  C4)(* + 0,2a2b3c4 +
C4)(* + 0,2a2b3c4 +  C8).
C8).
673. Уставте замість зірочки такий одночлен, щоб утворилася тотожність:
27а3 – 0,001с3 = (3а – *)(9а2 + 0,3ас + 0,01с2).
674. Подайте двочлен у вигляді добутку двох виразів:
1)216х3y9 – 0,125; 3)343с3 –  а18;
а18;
2) 27а6 – 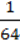 B12; 4) 64m3 – 1000n12.
B12; 4) 64m3 – 1000n12.
675. Подайте двочлен у вигляді добутку двох виразів:
1) 1000 – 0,008х6y6; 2) 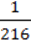 – 8c12d21; 3)64а24 – с33.
– 8c12d21; 3)64а24 – с33.
676. Спростіть вираз:
1) (а + 2b)(а2 – 2аb + 4b2)(а3 – b3);
2) (3х – y)(3х + y)(9Х2+ 3хy + у2)(9х2 – 3ху + у2);
3) (m – 0,1n)(m3 + 0,001n3)(m + 0,1 mn + 0,01n2).
677. Спростіть вираз:
1) (b + 4с)(b2 – 4bс + 16с2)(64с3 – b3);
2) (n3 + 0,125t3)(n2 + 0,5nt + 0,25t2)(n – 0,5t).
678. Спростіть вираз і знайдіть його значення:
1)(1 + х)(1 – х + х2)(1 – х3), якщо х = 2;
2) (2а – 5b)(4а2 + 10аb + 25b2) – 8а3, якщо а = 12,25, b = -0,1
679. Спростіть вираз:
1) (3 + b)3 – b3; 3)343у6 – (5 + 7у2)3;
2) (5 – 4а)3 + 64а3; 4) 125х3 – (5х + 1)3.
680. Спростіть вираз:
1) (а2с2 + 3ас)3 – а6с6; 3) (0,6m3 + n)3 – 0,216m9.
2) ( X2y + 5) – 125;
X2y + 5) – 125;
681. Обчисліть, не використовуючи калькулятор:
1) 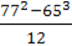 – (772 + 652);
– (772 + 652);
2) 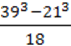 + 39 ∙ 21;
+ 39 ∙ 21;
3) 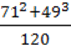 – 71 ∙ 49.
– 71 ∙ 49.
682. Доведіть, що:
1)793 -293 ділиться на 25.
2) 106 – 1 ділиться на 3.
683. Доведіть, що:
1)413 + 193 ділиться на 20;
2) 543 – 243 ділиться на 60
684. Розв’яжіть рівняння:
1) (1 + 2х)(4х2 – 2х + 1) – 4х(2х2 – 5) = 21;
2) (X + 3)(X2 – 3X + 9) – х(х – 4)(х + 4) = 59;
3) (х – 6)(х2 + 6х + 36) – х(х – 7)(х + 7) = 29;
4) (х – 5)(х2 + 5х + 25) – х(х – 3)2 = 2х(3х + 8).
685. Розв’яжіть рівняння:
1) (1 + х)(х2 – х + 1) – 0,04х(25х2 – 5) = 20;
2) (х – 3)(х2 + 3х + 9) – х(х – 1 )2 = 4х(0,5х + 6,5).
686. Ребро одного куба на 2 см більше за ребро іншого куба, а сума їх об’ємів дорівнює 152 см3. Знайдіть довжини ребер обох кубів.
687. Периметр основи одного куба на 12 см більший за периметр основи іншого куба, а різниця їх об’ємів дорівнює 117 см3. Знайдіть довжини ребер обох кубів.
688. Різниця периметрів основ двох кубів дорівнює 4 см, а сума їх об’ємів – 341 см3. Знайдіть відношення довжин ребер кубів.
689. Доведіть, що сума кубів двох послідовних натуральних чисел ділиться на 4.
690. Доведіть, що:
1) 3283 +1723 ділиться на 2000;
2) 7313 – 6113 ділиться на 120.
691. Два натуральні числа при діленні на 13 дають в остачі 1 і 3 відповідно. Доведіть, що різниця кубів цих чисел ділиться на 13.
692. Доведіть, що вираз (х2 – ху + у2)3 + (х2 + ху + у2)3 набуває невід’ємних значень при будь-яких числових значеннях змінних х і у.
693. Доведіть тотожність:
(x + y + z)3- х3 – у3- z3 = 3(x + y)(y + z)(x + z).
694. Доведіть, що х3 + х2у – ху2 + у2z + у3 = 0 , якщо x + y + z = 0.
695. Обчисліть:
1) значення виразу а3 + b3, якщо а + b = -3, ab = -10;
2) значення виразу а3 – b3, якщо b – a = 5, ab = 14
696. Для зберігання овочів тато виготовив ящик, що має форму куба з ребром 1 м. Проте ящик виявився завеликим Тато вирішив зменшити кожне ребро на 30 см. На скільки зменшився об’єм ящика? Який об’єм нового ящика?
697. Для виготовлення каркасних макетів двох кубів Сергій розрахував, що йому знадобиться 1,8 м і 1,44 м проволоки (не враховуючи потреб на закріплення згинів). Яке ребро в більшого і меншого кубів? Порівняйте їх об’єми.
698. Цукор і сіль мама зберігає в ємностях, які мають форму куба з ребрами 12 см і 8 см відповідно. На скільки більше за об’ємом мама зберігає цукру аніж солі?
ЗАДАЧІ НА ПОВТОРЕННЯ
699. Знайдіть значення виразу 3а2 + 10аb + 2b2.
1) якщо а = -2, b = 5; 2) якщо а = 13 , b =  .
.
700. Доведіть тотожність 5 (а – b) + 6(b – с) – 3(а – с) = 3(а – с) + (b – а) різними способами.
701. Туристична фірма у липні збільшила вартість путівки на 25 %, а в жовтні – зменшила на 10 %. Як змінилася вартість путівки?