ТЕОРЕТИЧНІ ВІДОМОСТІ
ПОВТОРЕННЯ
ТЕОРЕТИЧНІ ВІДОМОСТІ
ВИРАЗИ І ТОТОЖНОСТІ
Вирази | |
Числові | Буквені |
Запис, в якому використовують тільки числа, знаки арифметичних дій і дужки, називається числовим виразом. | Запис, в якому використовують змінні, позначені буквами, числа, знаки арифметичних дій і дужки, називається виразом зі змінними. |
24 : 4 + 5 або (12 – 2) ∙ 0,5 | (2 + а) : 30 або |
Означення | Приклад |
Цілий | 4а – 3b, 12х + 17, 3c – |
Усі значення змінної, допустимі для певного виразу, утворюють область допустимих значень (ОДЗ) змінної цього виразу.
Вираз | ОДЗ виразу |
| Х ≠ -12 |
| Х – будь-яке число |
| Х ≠ -7 і х ≠ 3 |
Два вирази називаються тотожно рівними, якщо вони набувають відповідно рівних значень за будь-яких
Означення | Приклад |
Тотожність – це рівність, ліва і права частини якої є тотожно рівними виразами | 10х – (6y – 3х) = 7х – 6y, А2 – b2 = (а + b)(а – b) |
Довести тотожність означає довести рівність її лівої і правої частин.
Способи доведення тотожностей
Назва способу | Сутність способу | Приклад |
Перетворення лівої частини рівності | Перетворити вираз у лівій частині даної рівності так, щоб він набув вигляду виразу в її правій частині | (a – 2b)(a + 2b)(a2 + 4b2) = а4 – 16у2 (а – 2b)(а + 2b)(а2 + 4b2) = (а2 – 4b2)(a2 + 4b2) = а4 – 16y2 |
Перетворення правої частини рівності | Перетворити вираз у правій частині даної рівності так, щоб він набув вигляду виразу в її лівій частині | (а – 2b)(а + 2b)(а2 + 4b2) = А4 – 16y2 А4 – 16у2 = = (а2 – 4b2)(а2 + 4b2) = = (а – 2b)(а + 2b)(а2 + 4b2) |
Перетворення обох частин рівності | Перетворити вирази в обох частинах даної рівності так, щоб вони набули одного й того самого вигляду | (а – 2b)(a + 2b)(а2 + 4b2) = а4 – 16y2 (а – 2b)(а + 2b)(а2 + 4b2) = (а2 – 4b2)(a2 + 4b2) А4 – 16у2 = (а2 – 4b2)(a2 + 4b2) |
Різницеве Порівняння | Перевірити, чи дорівнює нулю різниця виразів у лівій і правій частинах даної рівності | (а – 2b)(а + 2)(а2 + 4b2) = а4 – 16у2 (а – 2b)(а + 2b)(а2 + 4b2) – (а4 – 16) = (а2 – 4b2)(а2 + 4b2) – (а4 – 16y2) = (а4 – 16у2) – (а4 – 16у2) = 0 |
СТЕПЕНІ
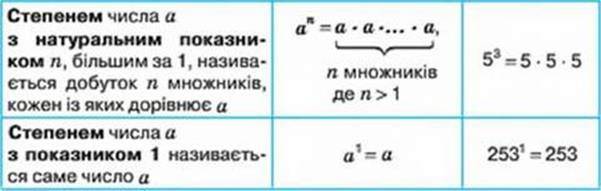
Будь-який натуральний степінь числа 1 дорівнює 1 | 1n = 1 | 12016 = 1 |
Будь-який натуральний степінь числа 0 дорівнює 0 | 0n = 0 | 02016 = 0 |
Будь-який натуральний степінь додатного числа – число додатне | Аn >0, якщо а >0, n – натуральне число | 48 > 0 |
Парний натуральний степінь від’ємного числа – число додатне | Аn > 0, якщо а < 0, n = 2k, k – натуральне число | (-4)8 > 0 |
Непарний натуральний степінь від’ємного числа – число від’ємне | Аn < 0, якщо а < 0, n = 2k – 1, K – натуральне число | (-4)9<0 |
Дії першого ступеня зі степенями
Переставна властивість | |
Аn + аm – = аm + аn | 52 + 53 = 53 + 52 150 = 150 |
Аn + bn = bn + an | 52 + 42 = 42 + 52 41 = 41 |
Для віднімання переставна властивість виконується не завжди | 52 – 53 ≠ 53 – 52 – 100 ≠ 100 |
52 – 42 ≠ 42- 52 9 ≠ -9 | |
Сполучна властивість | |
(an + am ) + аk = аn + (аm + аk ) | (52 + 53) + 54 = 52 + (53 + 54) 150 + 625 = 25 + 750 775 = 775 |
(аn + bn) + сn = аn + (bn + сn) | (32 + 42) + 52 = 32 + (42 + 52) 25 + 25 = 9 + 41 50 = 50 |
(аn – аm) – аk = аk – (аm + аk) | (52 – 53) – 54 = 52 – (53 + 54) -100 – 625 = 25 – 750 -725 = -725 |
(аn – bn) – сn = аn – (bn + сn) | (32 – 42) – 52 = 32 – (42 + 52) -7 – 25 = 9 – 41 – 32 = -32 |
Дії другого ступеня зі степенями
Переставна властивість | |
An ∙ am = am∙ an | 22 ∙ 23 = 23 ∙ 22 32 = 32 |
Аn ∙ bn= bn ∙ аn | 22 ∙ 42 = 42 ∙ 22 64 = 64 |
Для ділення переставна властивість виконується не завжди | 22 : 23 ≠ 23 : 22
|
22 : 42 ≠ 42 : 22
| |
Сполучна властивість | |
(аn ∙ аm) ∙ аk = аn ∙ (аm ∙ аk) | (22 ∙ 23) ∙ 24 = 22 ∙ (23 ∙ 24) 32 ∙ 16 = 4 ∙ 128 512 = 512 |
(an ∙ bn) ∙ cn = an ∙ (bn ∙ cn) | (32 ∙ 42) ∙ 22= З2 ∙ (42 ∙ 22) 144 ∙ 4 = 9 ∙ 64 576 = 576 |
Для ділення сполучна властивість виконується не завжди | (22 : 23) : 24 ≠ 22 : (23 : 24)
|
(32 : 42) : 22 ≠ 32 : (42 : 22)
| |
Розподільна властивість | |
(an + am) ∙ ak = anak + amak | (22 + 23) ∙ 24 = 22 ∙ 24 + 23 ∙ 24 12 ∙ 16 = 64 + 128 192 = 192 |
(аn + bn) ∙ сn = аnсn + bnсn | (32 + 42) ∙ 22 = 32 ∙ 22 + 42 ∙ 22 25 ∙ 4 = 36 + 64 100 = 100 |
(an + am) : ak = an : ak + am : ak, (a ≠ 0) | (22+23) : 24 = 22 : 24 + 23 : 24 12 : 16 =
|
(an + bn) : сn = аn : cn + bn : cn, (c ≠ 0) | (32 + 42) : 22 = 32 : 22 + 42 : 22 25 : 4 = 6 |
Властивість степенів із рівними основами | |
Аn ∙ аm = аn+m | 23 ∙ 22 = 23+2 = = 25= = 32 |
Аn : аm = аn-n, (n > m, a ≠ 0) | 23 : 22 = = 23-2 = = 21 = = 2 |
Властивість степенів із різними основами і рівними показниками | |
Аn ∙ bn = (аb)n | 32 ∙ 42= (3 ∙ 4)2= = 122= = 144 |
| 62 : 32 = (6 : 3)2= = 22 = = 4 |
Дія третього ступеня зі степенями | |
(am)n = аmn | (32)3 = 32 ∙ 3= = 36 = 729 |
ОДНОЧЛЕНИ
Цілий вираз, що є добутком чисел, змінних та їх натуральних степенів, називається одночленом.
Одночлен | Стандартний вигляд одночлена | Коефіцієнт Одночлена | Степінь Одночлена |
X | X | 1 | 1 |
3,5х3y | 3,5х3у | 3,5 | 3 +1 = 4 |
-x5y8ax | -ax6y8 | -1 | 1 + 8 + 6 =15 |
6x5y8∙ 0,5y2 | 3х5y10 | 3 | 5 + 10 = 15 |
5 | 5 | 5 | 0 |
Дії першого ступеня з одночленами
Переставна властивість | |
12х5 + у2 = у2 + 12х5 | 12х5 – у2 ≠ у2 -12х5 |
Сполучна властивість | |
(12х5 + у2) + 6х = 12х5 + (у2 + 6х) | (12х5 – у2) – 6х ≠ 12х5 – (y2 – 6х) (12х5 – у2) – 6х = 12х5 – (у2 + 6х) |
Дії другого ступеня з одночленами
Переставна властивість | |
12х5 ∙ у2 = у2 ∙ 12х5 | 12х5 : у2 ≠ у2 : 12х5 |
Сполучна властивість | |
(12х5 ∙ у2) ∙ 6х = 12х5 ∙ (у2 ∙ 6х) | (12х5 : у2) : 6х ≠ 12х5 : (y2 : 6х) (12х5 : у2) : 6х = 12х5 : (у2 ∙ 6х) |
Дія третього ступеня з одночленами
Правило | Приклад |
Щоб піднести одночлен до n-го степеня, треба піднести до цього степеня кожний множник даного одночлена та обчислити коефіцієнт отриманого одночлена | (0,5a7c2)2= = 0,52a7∙ 2c2 ∙ 2 = = 0,25а14с4 |
МНОГОЧЛЕНИ
Вираз, що є сумою кількох одночленів, називається многочленом.
Якщо многочлен подано в стандартному вигляді, то степенем цього многочлена називається степінь його старшого члена.
Многочлен | Стандартний вигляд Многочлена | Вільний член Многочлена | Старший Член многочлена | Степінь Многочлена |
X2 – 7x – 2 | Х2 – 7Х – 2 | -2 | X2 | 2 |
-х + 3 + 2х | Х + 3 | 3 | X | 1 |
5х2 – 1 + 5у – 3 | 5х2 + 5у – 4 | -4 | 5х2 | 2 |
Дії першого ступеня з многочленами
Переставна властивість | |
0,3х + (y2 + 2) = (у2 + 2) + 0,Зх | (12 – х) + (у2 + 2) = (у2 + 2) + (12 – х) |
0,3х -(у2 + 2) ≠ (у2 + 2) – 0,3х | (12- х) + (y2 + 2) = (у2 + 2) + (12 – х) |
Сполучна властивість | |
(0,3х + (у2 + 2))+ у2= = 0,3х + ((у2 + 2) + у2) | ((х + 3) + (у2 + 2)) + (1 – х) = (x + 3) + ((y2 + 2) + (1 – х)) |
(0,3х – (у2 + 2)) – у2= = 0,3х -((у2 + 2) + y2) | ((х + 3) – (у2 + 2)) – (1 – х)= = (х + 3) – ((1 – х) + (y2 + 2)) |
Множення многочленів
Одночлен | Означає скласти вираз, що є сумою добутків Кожного Члена Многочлена | І даного одночлена | Та спростити його, якщо це можливо |
Помножити Многочлен На | Многочлен | На кожен член іншого многочлена |
Формула множення одночлена на двочлен | Формула множення двочленів |
С(а + b) = са + сb | (а+ b)(c + d) – ac + ad + bc + bd |
12х5 – (у2 + 2)= = 12х5 – у2 + 12х5 ∙ 2 = = 12х5y2 + 24х5 | (12×5 – х) ∙ (у2 + 2)= = 12х5 ∙ y2 + 12х5 ∙ 2 – х ∙ у2 – х ∙ 2 = = 12х5у2 + 24х5 – ху2 – 2х |
Властивості множення многочленів
Переставна властивість | |
12х5 ∙ (у2 + 2) = (у2 + 2) ∙ 12х5 | (12х5 – х) ∙ (у2 + 2) = (у2 + 2) ∙ (12×5 – х) |
Сполучна властивість | |
((у2 + 2) ∙ 12х5) ∙ 6х = = (у2 + 2) ∙ (12х5 ∙ 6х) | ((х + 3) ∙ (у2 + 2)) ∙ (1 – х)= = (х + 3) ∙ ((у2 + 2) ∙ (1 – х)) |
Дія третього ступеня з многочленами
Правило | Приклад |
Щоб піднести многочлен до n-го степеня, треба помножити цей многочлен на себе п разів | (а + b)2 = (а + b)(а + b) (а + b)3 = (а + b)(а + b)(а + b) |
Формули скороченого множення
Формула | Приклад |
Квадрат двочлена: (а + b)2 = а2 + 2аb + b2 (а – b)2= а2 – 2аb + b2 | (2а + 3b)2= = (2а)2 + 2 ∙ 2а ∙ 3b + (3b)2 = = 4а2 + 12аb + 9b2 (5 – 6bс)2 = = 52 – 2 ∙ 5 ∙ 6bс + (6bс)2 = = 25 – 60bс + 36b2с2 |
Різниця квадратів: А2 – b2 = (а + b)(а – b) | 4х2 – 9у2 = (2х + 3у)(2х – 3у) |
Сума і різниця кубів: А3 + b3 = (а+ b)(а2 – ab + b2) А3 – b3 = (а – b)(a2 + ab + b2) | 125а3b3 + с3 = = (5аb + с) ∙ (25а2b2 – 5аbс + с2) 8х3 – 27у3 = = (2х – 3у) ∙ (4х2 + 6ху + 9y2) |
Розкладання многочленів на множники
Спосіб | Приклад |
Винесення спільного множника за дужки | 6х2y3 – 24х4у 3 + 18х3у2 = = 6х2у2(у – 4х2у + 3х) |
Застосування формул скороченого множення | 64х6y6 – х3y3= = х3у3(4ху – 1)(16x2y2 + 4ху + 1) |
Спосіб групування | 2х2у2 – 3ху + 4х3у3 – 6х2y2 = = ху((2ху – 3) + 2ху(2ху – 3)) = = ху(2ху -3)(1 + 2ху) |
Означення | Приклад |
Правило, згідно з яким кожному значенню незалежної змінної ставиться у відповідність єдине значення залежної змінної, називають функцією | У = f(x), наприклад, у = х2 + 5 У = F(х), наприклад, у = 2 – 5х 2 = g(t), наприклад, z = 3t3 + 1 X = ф(t), наприклад, х = 4,1 t – 2,7 |
Незалежну змінну називають аргументом функції, а залежну змінну – функцією | У = f(x) : х – аргумент, у – функція У = F(х): х – аргумент, у – функція Z = g(t) : t – аргумент, z – функція Х = ф(t) : t – аргумент, х – функція |
Усі можливі значення аргументу утворюють область визначення функції, а відповідні значення залежної змінної – область значень функції | У = х2 – 2x + 3: Область визначення – будь-які числа, область значень – будь-які числа у = |x|: Область визначення – будь-які числа, область значень – будь-які невід’ємні числа |
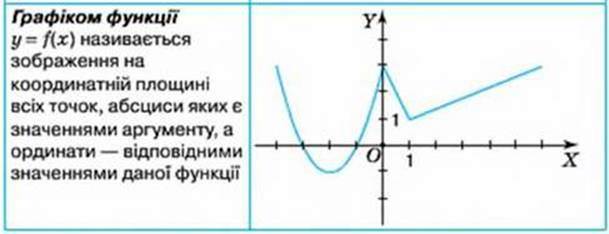
ФУНКЦІЇ
Функція вважається заданою, якщо:
1) задано область її визначення;
2) указано правило, згідно з яким для кожного значення аргументу можна знайти відповідне значення залежної змінної (функції).
Способи задания функції:
1) аналітичний;
2) описовий;
3) табличний;
4) графічний.


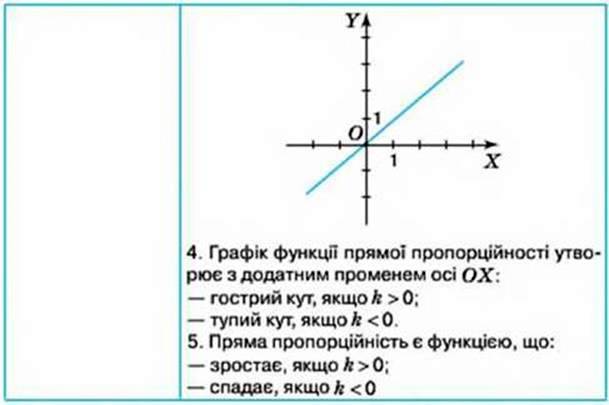
ЛІНІЙНІ РІВНЯННЯ ТА ЇХ СИСТЕМИ
Означення | Приклад |
Лінійним рівнянням з однією змінною називається рівняння виду ах + b = 0 , де х – змінна, a і b – деякі числа | 4х – 2 = 0, -12х + 48 = 0, 7х = 0 |
Розв’язування лінійних рівнянь з однією змінною
Значення А і b | Вигляд рівняння | Розв’язання | Кількість Коренів | Приклад |
A ≠ 0, b ≠ 0 | Aх + b= 0 | Ах = – b, Х= – | 1 корінь | 4х – 8 = 0, 4х = 8, Х = 2 |
A ≠ 0, b = 0 | Ах = 0 | Х= 0 : а, х = 0 | 1 корінь | 5х = 0, Х = 0 |
А = 0, b ≠ 0 | 0 ∙ х + b = 0 | 0 ∙ х = – b | Немає Коренів | 0х + 7 = 0, 0х = -7, Коренів немає |
A = 0, B = 0 | 0 ∙ x = 0 | 0 ∙ х = 0 | Безліч Коренів | 0х = 0, Безліч коренів |
Означення | Приклад |
Лінійним рівнянням із двома змінними називається рівняння виду ax + by + c = 0, де х і у – змінні, a, b і с – деякі числа | 2х – у + 6 = 0, Х + 3у – 7 = 0, 5х – 2у = 0 |
Гpафіком рівняння із двома змінними називається зображення на координатній площині всіх точок, координати яких задовольняють дане рівняння.
Побудова графіка рівняння із двома змінними
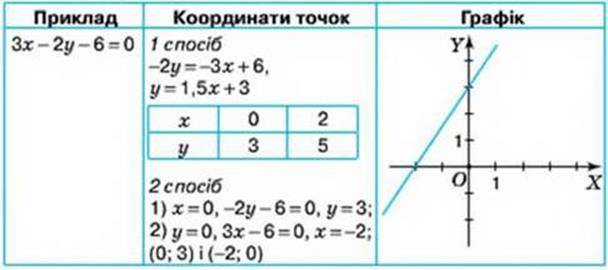
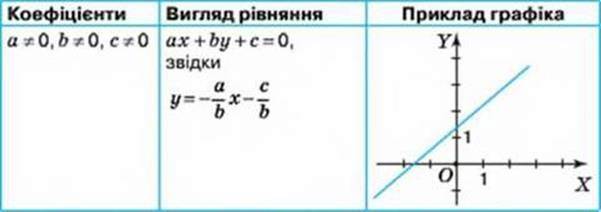
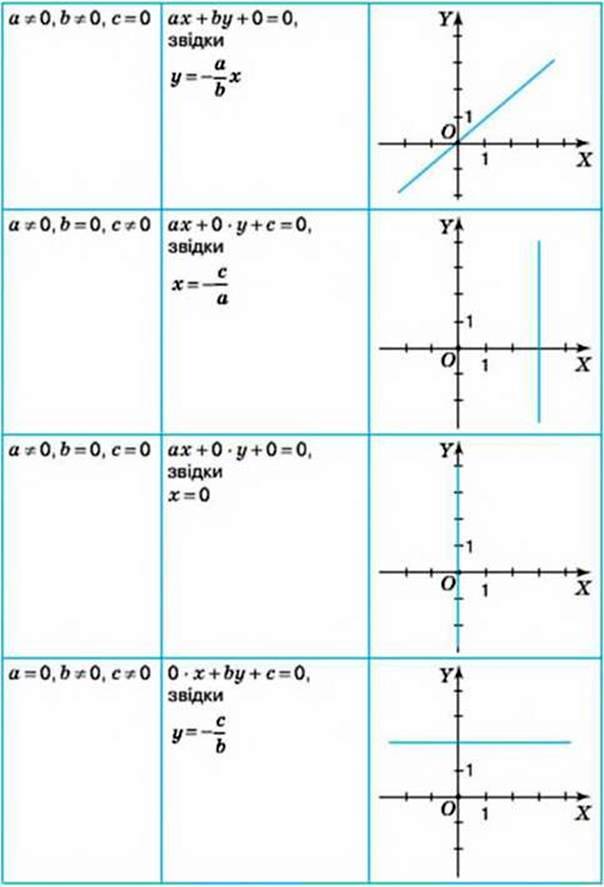
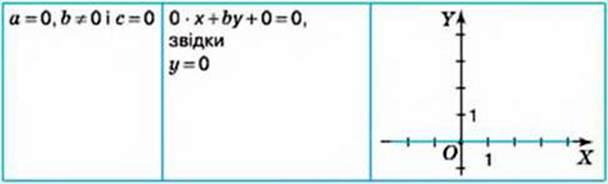
Гpафік лінійного рівняння із двома змінними ax + by + с = 0:
– є прямою, якщо або а ≠ 0, або b ≠ 0;
– є всією площиною, якщо а = 0, b = 0 і с = 0;
– не містить жодної точки координатної площини, якщо а = 0, b = 0 і с ≠ 0.
Розміщення на координатній площині прямої, що є графіком лінійного рівняння з двома змінними
Ах + bу + с = 0
Розв’язком системи двох лінійних рівнянь із двома змінними називають таку пару чисел (х; у), яка одночасно є розв’язком кожного рівняння системи.
Розв’язати систему рівнянь – означає знайти всі її розв’язки або встановити, що розв’язків немає.
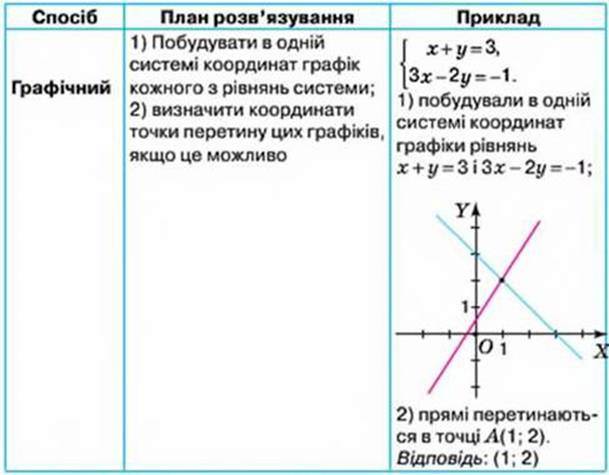
Види розв’язків системи двох лінійних рівнянь із двома змінними 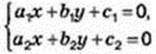
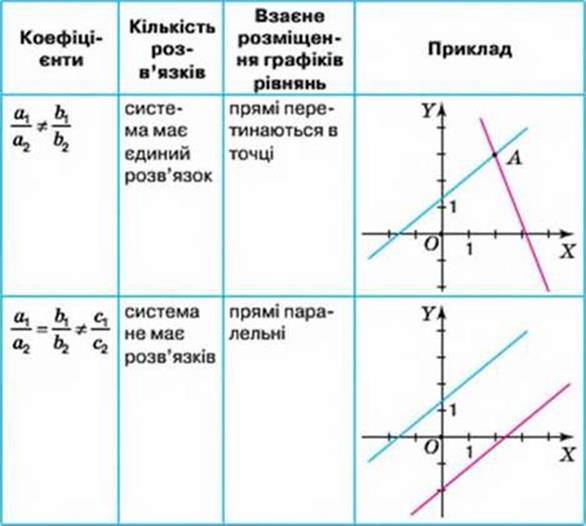
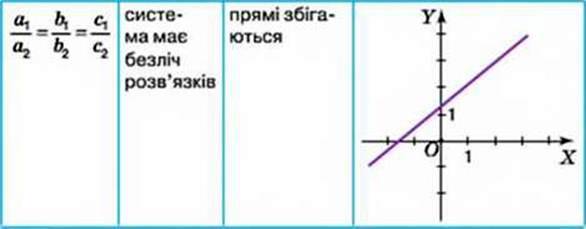
Способи розв’язування системи двох лінійних рівнянь із двома змінними:
1) графічний;
2) підстановки;
3) додавання.
Способи розв’язування системи двох лінійних рівнянь із двома змінними

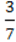 Х + 4 ,
Х + 4 ,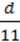
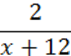
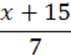
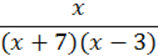
 ≠ 2
≠ 2 ≠ 4
≠ 4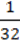 ≠ 8
≠ 8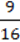 : 4 ≠ 9 : 4
: 4 ≠ 9 : 4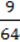 ≠ 2
≠ 2 =
=  + 4
+ 4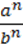 = (
= (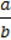 )n, (b ≠ 0)
)n, (b ≠ 0)