Тригонометричні функції числового аргументу
Математика – Алгебра
Тригонометричні функції
Тригонометричні функції числового аргументу
Розглянемо одиничне (тригонометричне) коло, центр якого розташований у точці  і радіус якого дорівнює 1 (див. рисунок).
і радіус якого дорівнює 1 (див. рисунок).
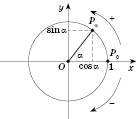
Нехай точка P0 – це точка (1; 0). Кожну іншу точку кола можна дістати поворотом P0 навколо початку координат. Будемо вважати від’ємним напрямок повороту за годинниковою стрілкою, додатним – проти.
Точку, яку дістанемо поворотом P0 навколо початку координат
 , назвемо
, назвемо  . Очевидно, що значення
. Очевидно, що значення  можуть бути від
можуть бути від  до
до 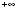 , причому кути, міри яких відрізняються на
, причому кути, міри яких відрізняються на 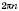 ,
, 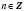 , дають на колі одну й ту саму точку. Наприклад:
, дають на колі одну й ту саму точку. Наприклад: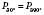 ,
, 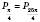 .
.Введемо означення:
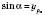 ;
; 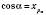 ;
;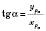 ;
; 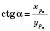 .
.Значення
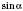 ,
, 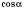
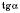 ,
, 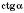 залежить тільки від кута
залежить тільки від кута  .
.Для
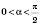 ці означення дають той самий результат, що й означення за допомогою елементів прямокутного трикутника.
ці означення дають той самий результат, що й означення за допомогою елементів прямокутного трикутника.Якщо означення
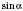 ,
, 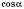 ,
, 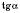 ,
, 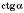 уведені таким чином, то очевидно, що ми дістали числові функції. Дійсно, кожному значенню
уведені таким чином, то очевидно, що ми дістали числові функції. Дійсно, кожному значенню 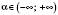 відповідає єдине значення
відповідає єдине значення 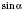 і
і 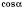 . Також кожному дійсному значенню
. Також кожному дійсному значенню 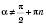 ,
, 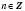 , відповідає єдине значення
, відповідає єдине значення 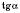 і кожному значенню
і кожному значенню 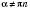 ,
,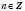 , відповідає єдине значення
, відповідає єдине значення 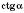 .
.Проведемо дотичну t до одиничного кола в точці
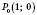 (див. рисунок нижче). Вона називається Лінією тангенсів, тому що ордината точки перетину прямої
(див. рисунок нижче). Вона називається Лінією тангенсів, тому що ордината точки перетину прямої 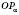 із прямою t дорівнює тангенсу кута
із прямою t дорівнює тангенсу кута 
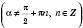 .
.Проведемо дотичну q до одиничного кола в точці
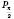 (див. рисунок на с. 73). Для довільного числа
(див. рисунок на с. 73). Для довільного числа 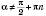 ,
,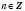 , абсциса точки перетину прямої
, абсциса точки перетину прямої 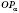 з прямою q дорівнює котангенсу кута
з прямою q дорівнює котангенсу кута  . Тому пряма q називається Лінією котангенсів.
. Тому пряма q називається Лінією котангенсів.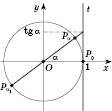
Співвідношення між тригонометричними функціями одного аргументу
1) 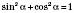 ;
;
2) 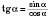
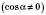 ;
;
3) 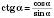
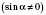 ;
;
4) 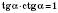
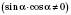 ;
;
5) 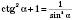
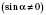 ;
;
6) 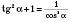
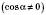 .
.
Основою для виведення решти формул є Формули додавання:
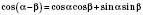 ;
;
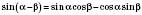 ;
;
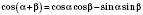 ;
;
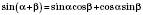 ;
;
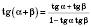 ;
;
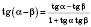 .
.
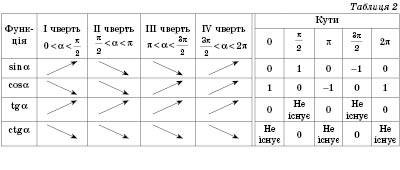
Формули зведення
Формули зведення допомагають виразити значення тригонометричних функцій кутів вигляду 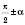 ,
, 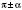 ,
,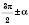 ,
, 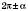 через функції кута
через функції кута  (табл. 1). Відповідні формули легко запам’ятати, користуючись такими правилами:
(табл. 1). Відповідні формули легко запам’ятати, користуючись такими правилами:
1) якщо аргумент функції має вигляд 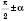 або
або 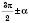 , назва функції змінюється на кофункцію (синус на косинус, тангенс на котангенс і навпаки), а якщо аргумент має вигляд
, назва функції змінюється на кофункцію (синус на косинус, тангенс на котангенс і навпаки), а якщо аргумент має вигляд 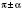 ,
,  , назва функції не змінюється;
, назва функції не змінюється;
2) перед утвореною функцією ставиться той знак, який має початкова функція, якщо  – кут у І чверті.
– кут у І чверті.
Використовуючи ці формули, а також періодичність тригонометричних функцій (див. нижче) можна значення тригонометричної функції довільного кута звести до значення функції гострого кута.
Формули суми і різниці однойменних тригонометричних функцій
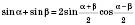 ;
;
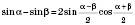 ;
;
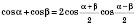 ;
;
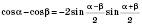 ;
;
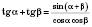 ;
;
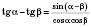 .
.
Формули перетворення добутку тригонометричних функцій на суму
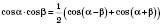 ;
;
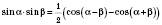 ;
;
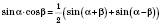 .
.
Формули подвійного аргументу
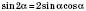 ;
;
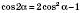 ;
;
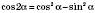 ;
;
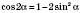 ;
;
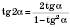 .
.
Формули половинного аргументу
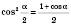 ;
; 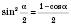 ;
;
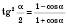 ;
; 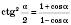 .
.
Формули перетворення синуса і косинуса кута через тангенс половини цього кута
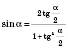 ;
; 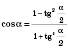 ;
;
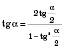 .
.