Головна ⇒ 📌Математика ⇒ Віднімання натуральних чисел

Віднімання натуральних чисел

Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ

§ 4. Віднімання натуральних чисел

Розглянемо задачу.

Задача 1. Пішохід за дві години пройшов 7 км. Скільки кілометрів він пройшов за другу годину, якщо за першу подолав 4 км?

У цій задачі число 7 є сумою числа 4 і невідомого числа: 4 + х = 7.

Дія, за допомогою якої за відомою сумою і одним з доданків знаходять другий доданок, називається відніманням.

Оскільки 4 + х = 7, то шуканий доданок х дорівнює 7 – 4. Записують так: 7 – 4 = 3. Отже, за другу годину пішохід пройшов

3 км.

Число, від якого віднімають, називається зменшуваним, а число, яке віднімають, – від’ємником. Результат віднімання називається різницею.

Отже:

Віднімання натуральних чисел

Додавання й віднімання – взаємно обернені дії. Тому віднімання завжди можна перевірити додаванням. 7 – 4 = 3. Перевірка: 3 + 4 = 7.

Оскільки a + 0 = a, то a – 0 = a і a – a = 0.

Різниця двох чисел показує, на скільки перше число більше за друге (або друге число менше від першого).

Віднімемо від числа 987 число 325. Для цього зменшуване і від’ємник розкладемо на розряди:

987 – 325 = (900 + 80 + 7) – (300 + 20 + 5).

Отже,

987 – 325

= (900 + 80 + 7) – (300 + 20 + 5) = (900 – 300) + (80 – 20) + (7 – 5) = 600 + 60 + 2 = 662.

Цим пояснюється віднімання натуральних чисел “стовпчиком”:

Віднімання натуральних чисел

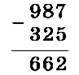
Розглянемо властивість віднімання суми від числа.

Задача 2. У класі 27 учнів. 12 з них займаються плаванням, а інших 7 – легкою атлетикою. Скільки

Учнів не займаються ні плаванням, ні легкою атлетикою? Відповідь можна отримати різними способами:

1-й спосіб. 27 – (12 + 7) = 27 – 19 = 8;

2-й спосіб. (27 – 12) – 7 = 15 – 7 = 8;

3-й спосіб. (27 – 7) – 12 = 20 – 12 = 8.

Щоб відняти суму від числа, можна від нього відняти один з доданків, а потім від результату відняти другий доданок.

У буквеному вигляді:

Віднімання натуральних чисел

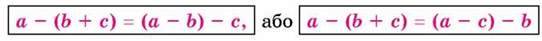
Розглянемо властивість віднімання числа від суми.

Задача 3. У ящику 7 білих кульок і 8 чорних. Учень взяв деякі 3 кульки. Скільки кульок залишилося в ящику? Відповідь можна отримати різними способами:

1-й спосіб. (7 + 8) – 3 = 12;

2-й спосіб. (7 – 3) + 8 = 12;

3-й спосіб. (8 – 3) + 7 = 12.

Щоб відняти число від суми, можна відняти і його від одного з доданків і до результату до

Дати другий доданок.

У буквеному вигляді:

Віднімання натуральних чисел

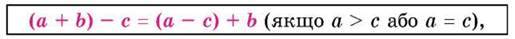
Або

Віднімання натуральних чисел

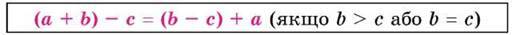
Розглянутими правилами зручно користуватися під час усних обчислень.

Приклади.

1) 225 – (125 + 37) = (225 – 125) – 37 = 100 – 37 = 73;

2) (432 + 729) – 232 = (432 – 232) + 729 = 200 + + 729 =929.

Початковий рівень

147. Прочитай приклади по-різному:

Віднімання натуральних чисел

148. Виконай віднімання і зроби перевірку:

1) 381 064 – 27 569; 2) 7 350 002 – 607 381.

149. Виконай віднімання і зроби перевірку:

1) 705 963 – 87 379; 2) 500 013 – 402 692.

150. Виконай віднімання:

1) 10 412 342 – 5 312 473;

2) 3 503 765 284 – 1 370 495 397;

3) 1 000 000 000 – 382 049 547;

4) 5 132 472 319 – 4 997 998 999.

151. Виконай віднімання:

1) 5 321 492 – 1 275 384;

2) 5 006 444 311 – 2 227 535 422;

3) 10 417 001 – 5 342 592;

4) 7 000 000 000 – 456 678 891.

Середній рівень

152. На скільки:

1) число 12 372 більше за число 7981;

2) число 342 512 менше від числа 457 891?

153. Зменш 5792 на 3983.

154. В одному мотку 129 м ниток для плетіння макраме, а в іншому – на 27 м менше. Скільки ниток у двох мотках?

155. Кіт Базиліо набрав 12 очок у баскетбольному матчі, а лисиця Аліса – на 3 очки менше. Скільки очок вони набрали разом?

156. Обчисли значення виразу:

1) a – 5792, якщо a = 8397; 10 000;

2) 35 492 – b, якщо b = 9001; 5993.

157. Том Сойєр і Гекльберрі Фін виграли разом у лотерею 327 гривень. Том виграв 159 гривень. Хто з друзів виграв більше і на скільки?

158. З двох полів зібрали 1380 т зерна – пшениці й жита. Пшениці зібрали 657 т. Чого зібрали більше (пшениці чи жита) і на скільки?

159. Виконай перевірку прикладу 23 – 5 = 18. Чи виконуються такі правила:

J 1) Якщо від зменшуваного відняти різницю, то отримаємо від’ємник.

2) Якщо до різниці додати від’ємник, то отримаємо зменшуване.

160. Обчисли:

1) 4006 – 2197 + 875;

2) 80 205 – 12 336 – 17 884;

3) 5 342 542 + (3 735 507 – 2 013 973);

4) 18 473 982 – (10 547 311 – 8 142 891).

161. Обчисли:

1) 47 105 + 29 895 – 57 937;

2) 115 397 – 96 588 – 2389;

3) 705 312 999 – (472 382 515 + 43 180 397);

4) 472 515 392 + (13 839 572 – 8 457 342).

162. Обчисли (усно) найзручнішим способом:

1) 78 – (45 + 18);

2) 547 – (20 + 47);

3) 98 – 13 – 28;

4) (400 + 735) – 200;

5) (547 + 329) – 247;

6) 593 – 90.

Достатній рівень

163. Як зміниться різниця 1527 – 381, якщо:

1) зменшуване збільшити на 15;

2) зменшуване зменшити на 73;

3) від’ємник збільшити на 24;

4) від’ємник зменшити на 83?

164. Заповни таблицю.

Зменшуване

Від’ємник

Різниця

4 273 517

2 311 549

497 857

257 381

3 517 219

417 591

165. 1) Власна швидкість катера – 27 км/год, а швидкість течії річки – 3 км/год. Знайди швидкість катера проти течії річки.

2) Швидкість катера за течією річки – 42 км/год, а швидкість течії річки – 2 км/год. Знайди швидкість катера проти течії річки.

166. Швидкість катера за течією 25 км/год, а власна швидкість катера 21 км/год. На скільки швидкість катера за течією більша за швидкість катера проти течії?

167. Постав у клітинки цифри так, щоб віднімання було виконано правильно:

Віднімання натуральних чисел

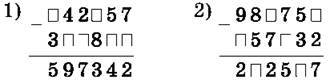
168. Постав цифри у клітинки так, щоб віднімання було виконано правильно:

Віднімання натуральних чисел

169. Мотузку завдовжки 5 м 16 см розрізали на три частини. Перша частина мала довжину 3 м 13 см,

Що на 2 м 23 см більше, ніж довжина другої частини. Знайди довжину третьої частини.

170. Альбом, зошит і ручка разом коштують 11 грн. 40 коп. Ручка коштує 2 грн. 70 коп., що на 90 коп. більше, ніж зошит. Скільки коштує альбом?

171. Три насоси викачали 115 л води з басейну. Перший і другий насоси разом викачали 72 л, а перший і третій разом – 67 л. Скільки літрів води викачав кожний насос окремо?

172. На трьох полицях разом 118 книжок. На першій і другій полицях разом 79 книжок, а решта – на третій, причому на третій полиці на 2 книжки більше, ніж на другій. Скільки книжок на кожній полиці?

173. Знайди значення виразу х + у + z:

Віднімання натуральних чисел

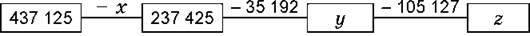
174. Магазин за 3 дні продав m кг яблук. За перший день продали 60 кг, а за другий – b кг. Скільки кілограмів яблук було продано за третій день? Склади буквений вираз і обчисли його значення, якщо m = 223, b = 83.

175. Протягом жовтня з баскетбольної секції пішло

7 учнів, а прийшло 12. Як змінилася кількість учнів у секції?

176. Знайди значення виразу, обираючи зручний порядок обчислення:

1) (7982 + 2001) – 4982;

2) (319 + 795) – 695;

3) 9372 – (1372 + 999);

4) 597 – (150 + 297).

177. Знайди значення виразу, обираючи зручний порядок обчислення:

1) (8957 + 5392) – 5957;

2) 14 582 – (5582 + 3500);

3) (18 397 + 13 152) – 8152;

4) 13 700 – (342 + 6700).

178. Використовуючи властивості віднімання, спрости вираз:

1) (93 + x) – 15; 2) (у + 327) – 100;

3) 59 – (m + 27); 4) 429 – (311 + k).

Розв’язання. 1) (93 + x) – 15 = (93 – 15) + x = 78 + x.

179. Використовуючи властивості віднімання, спрости вираз:

1) (37 + а) – 12; 2) (b + 415) – 300;

3) 42 – (x + 13); 4) 517 – (412 + у).

180. Знайди різницю, якщо:

1) зменшуване дорівнює від’ємнику;

2) зменшуване на п’ять одиниць більше за від’ємник.

181. Перевір правильність рівності а – (b – с) = = (а – b) + с, якщо а = 72, b = 33, с = 12.

182. Обчисли зручним способом, користуючись рівністю з попередньої вправи:

1) 589 – (189 – 30); 2) 7391 – (5291 – 42).

183. Перевір правильність рівності а + (b – с) = = (а – с) + b, якщо а = 48, b = 37, с = 11.

184. Обчисли зручним способом, користуючись рівністю з попередньої вправи:

1) 431 + (527 – 331); 2) 1278 + (352 – 178).

Високий рівень

185. Як зміниться різниця, якщо:

1) зменшуване збільшити на 5;

2) зменшуване зменшити на 7;

3) від’ємник збільшити на 2;

4) від’ємник зменшити на 4?

Розв’язання. 1) Розглянемо різницю a – b. Якщо зменшуване збільшити на 5, то маємо (а + 5) – b = (а – b) + 5, тобто різниця збільшилася на 5.

186. У фермерському господарстві число індиків більше за число курок на 297. Як змінилося це число, якщо:

Віднімання натуральних чисел

1) купили 15 індиків;

2) продали 18 індиків;

3)купили 23 курки;

4) продали 17 курок;

5) купили 18 індиків і 18 курок;

6) продали 17 індиків і 12 курок?

187. На зупинці з вагона метро вийшло 15 пасажирів, а ввійшло 23. На другій зупинці вийшло 17 пасажирів, а ввійшло 12. Скільки пасажирів було у вагоні метро до першої зупинки, якщо після другої зупинки їх стало 68?

188. Постав замість зірочок знак “+” чи “-” так, щоб виконувалася рівність:

1) 120 * 50 * 70 * 30 * 100 = 170;

2) 150 * 30 * 20 * 60 * 10 = 170.

189. Постав замість зірочок знак “+” чи “-“, щоб виконувалася рівність 54 * (32 * 17) * (43 * 11) = 37.

190. Як зміниться різниця, якщо:

1) зменшуване збільшити на 7, а від’ємник збільшити на 2;

2) зменшуване збільшити на 3, а від’ємник зменшити на 1;

3) зменшуване зменшити на 5, а від’ємник зменшити на 2;

4) зменшуване зменшити на 8, а від’ємник збільшити на 4?

Розв’язання. 4) Розглянемо різницю a – b. Якщо зменшуване зменшити на 8, а від’ємник збільшити на 4, то (a – 8) – (b + 4) = ((а – 8) – 4) – b = (а – (8 + 4)) – b = (а – 12) – b = (а – b) – 12.

Отже, різниця зменшилася на 12.

Вправи для повторення

191. Відстань між Києвом та Одесою 480 км. З них назустріч один одному виїхали два автобуси. Яка відстань буде між ними, коли один автобус проїде 217 км, а другий – на 5 км більше?

192. Заповни таблицю результатів змагань зі стрільби та визнач місце кожного учасника, якщо a = 6.

Учасники змагань

Вираз

Очки

Місце

Василь

9а – 7

47

Михайло

95 – 10а

Олександр

8а + 1

Петро

5а + 15

Віталій

88 – 8а

193. Обчисли та порівняй (>, =, <).

Віднімання натуральних чисел

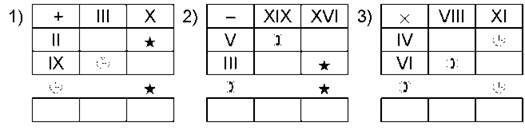
Домашня самостійна робота № 1

1. Запиши цифрами число 7 мільйонів 12 тисяч 4.

A) 7 120 004; Б) 7 12 004;

B) 7 012 004; Г) 7 012 040.

2. Яка із запропонованих нерівностей правильна?

A) 4132 > 4123; Б) 4143 < 4134;

B) 5017 > 5107; Г) 9541 < 9451.

3. Знайди суму 37 142 + 92 539.

А) 129 671; Б) 119 671; В) 129 681; Г) 119 671.

4. Яку з наведених цифр можна поставити замість зірочки у запис 37*8 < 3739, щоб утворилася правильна нерівність?

А) 3; Б) 5; В) 4; Г) 2.

5. Обчисли найзручнішим способом 456 + 3012 + + 2044.

А) 6512; Б) 5512; В) 5412; Г) 5500.

6. В одній цистерні 52 л бензину, а в іншій – на 18 л менше. Скільки літрів бензину у двох цистернах разом?

А) 96 л; Б) 122 л; В) 76 л; Г) 86 л.

7. Запиши число, яке на 4 менше від найменшого

П’ятицифрового числа.

А) 99 995; Б) 9996; В) 10 004; Г) 9997.

8. Скільки є натуральних чисел, замінивши якими букву а, отримаємо правильну подвійну нерівність 417 < а < 428?

А) 9; Б) 10; В) 11; Г) безліч.

9. Як зміниться різниця 5781 – 319, якщо від’ємник збільшити на 18?

A) зменшиться на 18; Б) збільшиться на 18;

B) не зміниться; Г) зменшиться на 36.

10. Сіндбад записав кілька послідовних натуральних чисел у порядку зростання. Число 36 стоїть п’ятим, якщо рахувати як з одного, так і з іншого боку. Якою є різниця між найбільшим і найменшим із записаних чисел?

А) 9; Б) 7; В) 8; Г) 10.

11. Знайдіть суму найбільшого і найменшого трицифрових чисел, записаних за допомогою цифр 1, 4, 5, якщо цифри у кожному із чисел не повторюються.

А) 686; Б) 695; В) 596; Г) 560.

12. Сума деяких двох натуральних чисел дорівнює 631. Якого найбільшого значення може досягати менше із цих чисел?

А) 310; Б) 316; В) 314; Г) 315.

Завдання для перевірки знань № 1 (§1- §4)

1. Порівняй числа:

1) 431 002 і 429 798; 2) 12 311 015 і 12 311 019.

12. Виконай додавання: 7 382 954 + 8 947 527.

3. Виконай віднімання: 13 152 973 – 9 189 858.

4. Порівняй:

1) 8000 г і 8 кг; 2) 7 км і 6993 м.

5. Виконай додавання, обираючи зручний порядок дій:

1) (473 + 152) + 527; 2) 538 + 263 + 212 + 37.

6. У першому ящику 57 кг картоплі, а в другому – на 12 кг менше. Скільки кілограмів картоплі у двох ящиках разом?

7. Яке найбільше і яке найменше чотирицифрові числа можна написати, використовуючи по одному разу цифри 5, 7, 0 і 3?

8. Обчисли значення виразу, обираючи зручний порядок дій:

1) (4897 + 7321) – 2897; 2) 9795 – (3002 + 4795).

9. У числах кілька цифр замінено на зірочки. Порівняй ці числа:

1) 43** і 47**; 2) *99 і 11**; 3) 94* і *398.

10. Додаткове завдання1. Знайди закономірність

І продовж ряд чисел (запиши три наступні числа ряду):

1) 3259, 3262, 3265, 3268, 3271;

2) 4215, 4212, 4214, 4211, 4213.

11. Додаткове завдання. Встав замість * знаки “+” і “-” так, щоб виконувалася рівність:

115 * 25 * 35 * 45 * 70 * = 150.

1 Додаткові завдання призначено для учнів, у яких залишається час після виконання основної роботи. Правильні розв’язання цих завдань вчитель може оцінювати окремою оцінкою.


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Віднімання натуральних чисел Урок № 11 Тема: Віднімання натуральних чисел Мета. Удосконалювати уміння і навички учнів на віднімання натуральних чисел при розв’язуванні прикладів і задач; розвивати пам’ять, увагу, логічне і аналітичне мислення, кмітливість, творчість; виховувати працелюбність, реалізуючи принцип виховання в колективі і через колектив. Обладнання: графо-проектор. Хід уроку І. Контроль, корекція, закріплення знань. 1. Домашні задачі груп А […]...

  2. Strong>Віднімання натуральних чисел. Властивості дії віднімання 4. Додавання і віднімання багатоцифрових чисел Віднімання натуральних чисел. Властивості дії віднімання Зменшення числа на зазначену кількість одиниць здійснюється дією віднімання. Віднімання – це дія, коли за сумою двох доданків і одним із них знаходять другий доданок. 344. 784 – 383 510 – 319 714 – 520 6000 – 600 + 6 918 – 543 […]...

  3. Віднімання натуральних чисел. Властивості віднімання УРОК 23 Тема. Віднімання натуральних чисел. Властивості віднімання Мета: закріпити засвоєння учнями означення віднімання двох натуральних чисел, властивостей нуля під час віднімання та знання властивостей віднімання натуральних чисел; завершити відпрацювання навичок застосування названих знань; перевірити рівень засвоєння навчального матеріалу. Тип уроку: застосування знань, навичок та вмінь. Обладнання: схема-таблиця “Віднімання натуральних чисел. Властивості віднімання”. Хід уроку […]...

  4. ОКРУГЛЕННЯ ЧИСЕЛ. ПРИЙОМИ ДОДАВАННЯ Й ВІДНІМАННЯ ЧИСЕЛ ПОВТОРЕННЯ МАТЕРІАЛУ ЗА 3 КЛАС ОКРУГЛЕННЯ ЧИСЕЛ. ПРИЙОМИ ДОДАВАННЯ Й ВІДНІМАННЯ ЧИСЕЛ 30. Випиши спочатку розрядні числа, потім круглі. Прочитай числа, які не є круглими. Чи всі розрядні числа є круглими? 700 320 500 784 30 640 300 325 400 115 31. У господаря 189 кущів винограду. Що точніше: у господаря приблизно 1 сотня чи […]...

  5. Додавання і віднімання натуральних чисел. Вирази УРОК 27 Тема. Додавання і віднімання натуральних чисел. Вирази Мета: перевірити засвоєння учнями теми “Додавання і віднімання натуральних чисел. Вирази”. Тип уроку: перевірка та корекція знань, навичок та вмінь. Хід уроку Тематична контрольна робота № 2 Варіант 1 1. Обчисліть: 1) 5 693 + 29 758; 2) 42 735 – 4 028. 2. На одній […]...

  6. Одиниці часу. Додавання і віднімання іменованих чисел Одиниці часу. Додавання і віднімання іменованих чисел 1 Згадай відомі тобі одиниці часу. Як вони співвідносяться? 2 Знайди дріб від числа. 3 Знайди число за величиною його дробу, якщо його: Становлять 72 с; Становлять 84 хв; 15 Становлять 90 год; З Становлять 1 рік. 4 Заміни більші одиниці часу меншими. 5 Заміни менші одиниці часу […]...

  7. ПИСЬМОВЕ ДОДАВАННЯ Й ВІДНІМАННЯ ЧИСЕЛ ПОВТОРЕННЯ МАТЕРІАЛУ ЗА 3 КЛАС ПИСЬМОВЕ ДОДАВАННЯ Й ВІДНІМАННЯ ЧИСЕЛ 39. Розв’яжи задачу складанням виразу. У хорі Будинку творчості 85 дітей, у гуртку з моделювання на 39 дітей менше, ніж у хорі, а в танцювальних колективах на 19 дітей більше, ніж у хорі й гуртку з моделювання разом. Скільки дітей займаються в танцювальних колективах? 40. […]...

  8. ДІЯ ВІДНІМАННЯ. НАЗВИ КОМПОНЕНТІВ І РЕЗУЛЬТАТУ ДІЇ ВІДНІМАННЯ. ЗНАХОДЖЕННЯ РІЗНИЦІ ЧИСЕЛ ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 42. ДІЯ ВІДНІМАННЯ. НАЗВИ КОМПОНЕНТІВ І РЕЗУЛЬТАТУ ДІЇ ВІДНІМАННЯ. ЗНАХОДЖЕННЯ РІЗНИЦІ ЧИСЕЛ Мета: розкрити суть дії віднімання; вчити учнів складати, читати й розв’язувати рівності на віднімання за малюнками і числовим променем; розвивати мислення; виховувати старанність. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. […]...

  9. ДОДАВАННЯ І ВІДНІМАННЯ КРУГЛИХ БАГАТОЦИФРОВИХ ЧИСЕЛ ЗАСТОСУВАННЯ НУМЕРАЦІЇ ДО ВИКОНАННЯ ДІЙ ДОДАВАННЯ І ВІДНІМАННЯ КРУГЛИХ БАГАТОЦИФРОВИХ ЧИСЕЛ 496. 5 тис. + 4 тис. 2 сот. + 9 сот. 30 дес. + 20 дес. 5 000 + 4 000 8 сот. – 3 сот. 12 сот. – 3 сот. 3 800 + 1 000 3 800 + 100 3 800 + 20 […]...

  10. Додавання і віднімання мішаних чисел Розділ 2 Звичайні дроби §11. Додавання і віднімання мішаних чисел Переставна та сполучна властивості додавання дають можливість звести додавання мішаних чисел до додавання їх цілих частин і додавання їх дробових частин. Якщо при додаванні дробових частин отримуємо неправильний дріб, то у цьому разі з нього виділяють цілу частину і додають її до цілої частини, яка […]...

  11. ЗАКРІПЛЕННЯ ДОДАВАННЯ І ВІДНІМАННЯ ДВОЦИФРОВИХ ЧИСЕЛ. САМОСТІЙНА РОБОТА УСНЕ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ У МЕЖАХ 100 З ПЕРЕХОДОМ ЧЕРЕЗ РОЗРЯД Урок 48. ЗАКРІПЛЕННЯ ДОДАВАННЯ І ВІДНІМАННЯ ДВОЦИФРОВИХ ЧИСЕЛ. САМОСТІЙНА РОБОТА Мета: удосконалити навички додавання і віднімання двоцифрових чисел; закріпити вміння розв’язувати задачі на дві дії; розвивати математичне мовлення; виховувати інтерес до математики, самостійність. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. […]...

  12. Арифметичні дії додавання і віднімання Арифметичні дії додавання і віднімання 1 Обчисли. 2 Згадай закони додавання; правила додавання і віднімання. Визнач без обчислень істинність або хибність поданих рівностей. Поясни свої міркування. 5 867 – (1 329 + 2 867) = (5 867 – 2 867) – 1 329 (32 405 + 16 000) + 14 000 = 32 405 + […]...

  13. Віднімання раціональних чисел. Властивості віднімання Урок № 7 4 Тема. Віднімання раціональних чисел. Властивості віднімання Мета: доповнити уявлення учнів властивостями віднімання; відпрацювати навички замінювати віднімання додаванням і знаходити значення утворених сум. Тип уроку: застосування знань, навичок та вмінь. Хід уроку І. Перевірка домашнього завдання Математичний диктант Варіант 1 [2] 1. Закінчіть речення: “Щоб від числа [а] відняти число 7 [-6], […]...

  14. ДІЯ ВІДНІМАННЯ. ПРАВИЛО ВІДНІМАННЯ СУМИ ВІД ЧИСЛА. ТАБЛИЧНЕ Й ПОЗАТАБЛИЧНЕ, УСНЕ І ПИСЬМОВЕ ВІДНІМАННЯ. ЗАДАЧІ, ЯКІ РОЗВ’ЯЗУЮТЬСЯ ВІДНІМАННЯМ Мета: узагальнити уявлення учнів про дію віднімання; закріпити вміння розв’язувати задачі на віднімання; повторити прийоми письмового віднімання трицифрових чисел; розвивати мислення; виховувати інтерес до предмета. ХІД УРОКУ I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. КОНТРОЛЬ, КОРЕКЦІЯ І ЗАКРІПЛЕННЯ ЗНАНЬ 1. Перевірка домашнього завдання 2. Усні обчислення Гра “Хто швидше?” 1-ша група 2-га група 3-тя група 3. Математичний диктант […]...

  15. Додавання натуральних чисел. Властивості додавання Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 3. Додавання натуральних чисел. Властивості додавання З початкових класів відомо, як додавати невеликі натуральні числа. Розглянемо задачу. Задача. У 5-А класі 27 учнів, а в 5-Б – 29 учнів. Скільки учнів у двох класах? Розв’язання. 27 + 29 = 56. Ця задача […]...

  16. Множення натуральних чисел Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 5. Множення натуральних чисел Як відомо з молодших класів, суму однакових доданків можна записати коротше за допомогою множення. Наприклад: 45 + 45 + 45 + 45 = 45 ∙ 4 = 180. Читають так: “по 45 взяти 4 рази” або “45 помножити […]...

  17. Ділення натуральних чисел Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 8. Ділення натуральних чисел Розглянемо задачу. Задача. 48 олівців розклали порівну в 6 коробок. Скільки олівців у кожній коробці? Розв’язання. Нехай у кожній коробці по х олівців. Тоді х ∙ 6 = 48. Тільки одне число при множенні на 6 дає 48. […]...

  18. Ряд натуральних чисел Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 1. НАТУРАЛЬНІ ЧИСЛА Вивчивши матеріал цього параграфа, ви розширите свої знання про натуральні числа та форму їх запису, навчитеся зручного способу порівняння натуральних чисел, дізнаєтеся, що таке координатний промінь і як можна позначати на ньому точками натуральні числа. Ознайомитеся з властивостями прямої, променя і відрізка. 1. […]...

  19. Strong>Додавання натуральних чисел. Властивості дії додавання 4. Додавання і віднімання багатоцифрових чисел Додавання натуральних чисел. Властивості дії додавання Будь-які два натуральні числа можна додати. Додавання – це арифметична дія, за допомогою якої знаходять число, що складається зі стількох одиниць, скільки їх є в усіх доданках разом. Сума натуральних чисел завжди більша від кожного з доданків. Для швидкого і раціонального обчислення треба […]...

  20. Додавання і віднімання іменованих чисел Додавання і віднімання іменованих чисел Способи додавання і віднімання складених іменованих чисел 1 Виконай обчислення письмово, перевір результати. 736 108 + 198 302 947 001 – 48 503 33 709 + 66 271 300 040 – 34 072 56 723 + 287 277 500 000 – 208 322 2 Заміни складені іменовані числа простими іменованими. […]...

  21. Порівняння натуральних чисел Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 2. Порівняння натуральних чисел Одне з двох різних натуральних чисел завжди більше або менше від іншого. Це означає, що натуральні числа можна порівнювати. Число 5392 більше за число 837 тому, що 5392 – чотирицифрове число, а 837 – трицифрове. Числа 5392 і […]...

  22. ПЕРЕВІРКА ДОДАВАННЯ Й ВІДНІМАННЯ ЧИСЕЛ ДІЇ З БАГАТОЦИФРОВИМИ ЧИСЛАМИ. ПИСЬМОВЕ ДОДАВАННЯ І ВІДНІМАННЯ ПЕРЕВІРКА ДОДАВАННЯ Й ВІДНІМАННЯ ЧИСЕЛ 571. Чи утворюють числа 17 359, 2 568 і 19 927 при додаванні і відніманні “родину”? Як пов’язані між собою дії додавання і віднімання? 572. Пригадай способи: А) перевірки додавання. 1. а + b = b + а 2. 3. прогнозування результату […]...

  23. Письмове додавання й віднімання трицифрових чисел. Знаходження значень буквених виразів. Задачі на 3 дії УРОК 3 Тема. Письмове додавання й віднімання трицифрових чисел. Знаходження значень буквених виразів. Задачі на 3 дії Мета: повторити алгоритм письмового додавання й віднімання чисел; опрацювати розширену задачу на знаходження третього доданка; ознайомити учнів з розміщенням відрізків на площині і в просторі. Обладнання: предметні малюнки, таблиця “Додавання й віднімання трицифрових чисел”. ХІД УРОКУ I. Контроль […]...

  24. НАЗВИ ЧИСЕЛ ПРИ ВІДНІМАННІ. ПЕРЕВІРКА ВІДНІМАННЯ ДОДАВАННЯМ. ЗНАХОДЖЕННЯ ЗНАЧЕНЬ ВИРАЗІВ З БУКВЕНИМИ КОМПОНЕНТАМИ. ПЕРИМЕТР ТРИКУТНИКА Мета: узагальнити знання учнів про практичне застосування зв’язку дій віднімання і додавання для перевірки обчислень; закріплювати вміння обчислювати значення виразів з буквеними даними; знаходити периметр трикутника; вдосконалювати обчислювальні навички; розвивати логічне мислення, увагу; виховувати старанність. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ (додаток) 1. Перевірка домашнього завдання 2. Гра “Хто швидше?” 3. Математичний […]...

  25. ВІДНІМАННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ Розділ 4 РАЦІОНАЛЬНІ ЧИСЛА ТА ДІЇ З НИМИ § 27. ВІДНІМАННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ Ви вже вмієте віднімати додатні числа і можете знайти різницю, коли зменшуване більше за від’ємник або дорівнює йому. ? Чи можна від меншого числа відняти більше? Так, якщо діємо з раціональними числами. Поміркуємо, спираючись на координатну пряму. Нехай треба знайти різницю чисел […]...

  26. НУМЕРАЦІЯ ЧИСЕЛ 1-100. ВИПАДКИ ДОДАВАННЯ І ВІДНІМАННЯ В МЕЖАХ 100, ПОВ’ЯЗАНІ З НУМЕРАЦІЄЮ ЧИСЕЛ. РОЗВ’ЯЗУВАННЯ ПРОСТИХ ЗАДАЧ ПОВТОРЕННЯ МАТЕРІАЛУ ЗА 1-Й КЛАС Урок 1. НУМЕРАЦІЯ ЧИСЕЛ 1-100. ВИПАДКИ ДОДАВАННЯ І ВІДНІМАННЯ В МЕЖАХ 100, ПОВ’ЯЗАНІ З НУМЕРАЦІЄЮ ЧИСЕЛ. РОЗВ’ЯЗУВАННЯ ПРОСТИХ ЗАДАЧ Мета: повторити нумерацію чисел 1-100; вдосконалити обчислювальні навички, вміння розв’язувати прості задачі; розвивати кмітливість, мислення учнів; виховувати інтерес до математики. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Ознайомлення […]...

  27. Віднімання раціональних чисел Урок № 7 3 Тема. Віднімання раціональних чисел Мета: сформувати уявлення учнів про зміст дії віднімання раціональних чисел; а також виробити вміння застосовувати це правило для розв’язування вправ, що передбачають виконання раціональних чисел. Тип уроку: засвоєння знань, умінь, навичок. Хід уроку І. Перевірка домашнього завдання @ Збираємо зошити на перевірку, виконавши попередньо невелику самостійну роботу […]...

  28. ДОДАВАННЯ 0 І ДО 0. ВІДНІМАННЯ 0 І РІВНИХ ЧИСЕЛ. КРУГ. РОЗПІЗНАВАННЯ ГЕОМЕТРИЧНИХ ФІГУР ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 35. ДОДАВАННЯ 0 І ДО 0. ВІДНІМАННЯ 0 І РІВНИХ ЧИСЕЛ. КРУГ. РОЗПІЗНАВАННЯ ГЕОМЕТРИЧНИХ ФІГУР Мета: ознайомити учнів із властивостями додавання й віднімання 0, віднімання рівних чисел; розвивати мислення; виховувати інтерес до математики. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. ПОВТОРЕННЯ ВИВЧЕНОГО […]...

  29. УТВОРЕННЯ, ЧИТАННЯ ТА ЗАПИСУВАННЯ П’ЯТИЦИФРОВИХ ЧИСЕЛ У МЕЖАХ 20 000. ПИСЬМОВЕ ДОДАВАННЯ І ВІДНІМАННЯ ТРИЦИФРОВИХ ЧИСЕЛ. НЕРІВНОСТІ ОРІЄНТОВНА НАВЧАЛЬНА МЕТА: ОЗНАЙОМИТИ З УТВОРЕННЯМ, ЧИТАННЯМ ТА ЗАПИСОМ П’ЯТИЦИФРОВИХ ЧИСЕЛ У МЕЖАХ 20 000; ПОВТОРИТИ ПИСЬМОВЕ ДОДАВАННЯ І ВІДНІМАННЯ ТРИЦИФРОВИХ ЧИСЕЛ; ФОРМУВАТИ ВМІННЯ ЗНАХОДИТИ ЗНАЧЕННЯ НЕВІДОМИХ У НЕРІВНОСТЯХ; УДОСКОНАЛЮВАТИ ВМІННЯ ПОРІВНЮВАТИ ЗАДАЧІ I. Перевірка домашнього завдання Взаємоперевірка учнями виконаних завдань один у одного в парах. II. Актуалізація та корекція опорних знань учнів 1. Завдання […]...

  30. Strong>Множення натуральних чисел 5. Множення і ділення багатоцифрових чисел Множення натуральних чисел 519. Обчисли. 16 + 16 + 16 14 + 14 + 14 + 14 + 14 + 14 19 + 19 + 19 + 19 + 19 + 19 + 19 + 19 520. Поясни складання рівностей. 15 + 15 + 15 + 15 = 15 […]...

  31. ТАБЛИЦЯ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ. РОЗВ’ЯЗУВАННЯ ЗАДАЧ ЗА ПЛАНОМ ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ. ЗАДАЧІ НА ДВІ ДІЇ. ВИРАЗИ З ДУЖКАМИ ЗАДАЧІ НА ДВІ ДІЇ Урок 25. ТАБЛИЦЯ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ. РОЗВ’ЯЗУВАННЯ ЗАДАЧ ЗА ПЛАНОМ Мета: узагальнити знання таблиць додавання і віднімання чисел; формувати вміння розв’язувати задачі за планом; виховувати пізнавальний інтерес до вивчення математики. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ […]...

  32. Strong>Ділення натуральних чисел 5. Множення і ділення багатоцифрових чисел Ділення натуральних чисел Пригадай, як називаються компоненти при діленні. 658. Поясни записи обчислень у стовпчиках. Дії множення і ділення є взаємно оберненими. 659. Прочитай вирази по-різному. 91 : 3 84 : 16 100 : 2 77 : 11 У множині натуральних чисел дія ділення не завжди виконується. Міркуй так. […]...

  33. ДОДАВАННЯ І ВІДНІМАННЯ БАГАТОЦИФРОВИХ ЧИСЕЛ НА ОСНОВІ НУМЕРАЦІЇ ЗАСТОСУВАННЯ НУМЕРАЦІЇ ДО ВИКОНАННЯ ДІЙ ДОДАВАННЯ І ВІДНІМАННЯ БАГАТОЦИФРОВИХ ЧИСЕЛ НА ОСНОВІ НУМЕРАЦІЇ 487. Назви класи і розряди чисел. Прочитай. 21 793 57 638 8 774 178 315 564 28 488. Використовуючи склад числа за класами і взаємозв’язок додавання і віднімання, виконай дії. 568 000 + 135 46 000 + 100 342 284 – 284 […]...

  34. Величини. Метрична система мір. Додавання й віднімання багатоцифрових чисел УРОК 130 Тема. Величини. Метрична система мір. Додавання й віднімання багатоцифрових чисел Мета: узагальнити й систематизувати знання учнів про дії додавання й віднімання багатоцифрових чисел, їх закони; вдосконалювати навички усної лічби. ХІД УРОКУ I. Контроль і закріплення знань учнів Усні обчислення – Обчислити зручним способом. 130 + 250 + 170 + 250 147 – (47 […]...

  35. СПОСОБИ ДОДАВАННЯ І ВІДНІМАННЯ ДВОЦИФРОВИХ ЧИСЕЛ. ПОРІВНЯННЯ ВИРАЗУ І ЧИСЛА ПОВТОРЕННЯ МАТЕРІАЛУ ЗА 1-Й КЛАС Урок 7. СПОСОБИ ДОДАВАННЯ І ВІДНІМАННЯ ДВОЦИФРОВИХ ЧИСЕЛ. ПОРІВНЯННЯ ВИРАЗУ І ЧИСЛА Мета: повторити способи додавання і віднімання двоцифрових чисел; формувати вміння порівнювати вирази і числа; розвивати логічне мислення; формувати потребу розв’язувати поставлені завдання швидко і правильно. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ Пролунав уже дзвінок, Всіх покликав на урок. Тому […]...

  36. Ряд натуральних чисел УРОК 3 Тема. Ряд натуральних чисел Мета: узагальнити і поглибити знання учнів про натуральні числа; формувати вміння розпізнавати натуральні числа, наводити їх приклади. Тип уроку: засвоєння нових знань. Хід уроку I. Актуалізація опорних знань @ Оскільки тема не є новою для п’ятикласників, доцільно провести з учнями бесіду: – Скільки тобі років? – Скільки кольорів у […]...

  37. ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ. ЗАДАЧІ НА ДВІ ДІЇ. ВИРАЗИ З ДУЖКАМИ ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ 82. Поясни прийоми додавання і віднімання чисел з переходом через розряд. Перевір результати обчислень за таблицями. Розкажи їх із пам’яті. 83. 11 – 2 – 4 14 – 5 + 2 14 – 10 + 6 39 – […]...

  38. ВІДНІМАННЯ ДВОЦИФРОВИХ ЧИСЕЛ З ПЕРЕХОДОМ ЧЕРЕЗ РОЗРЯД ВИДУ 34-18. РОЗВ’ЯЗУВАННЯ ЗАДАЧ Мета: повторити способи віднімання двоцифрових чисел з переходом через розряд; формувати в учнів уміння розв’язувати задачі; вдосконалювати обчислювальні навички; сприяти розвитку творчих здібностей. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Перевірка домашнього завдання (с. 156, завдання 25; 26) Завдання 25 – Скільком людям він побажав щастя? На скільки більше дітей, ніж дорослих […]...

  39. ПОРІВНЯННЯ ТРИЦИФРОВИХ ЧИСЕЛ ПОВТОРЕННЯ МАТЕРІАЛУ ЗА 3 КЛАС ПОРІВНЯННЯ ТРИЦИФРОВИХ ЧИСЕЛ 1. 324 > 89, трицифрове число більше від двоцифрового. 2. 571 > 498, із двох трицифрових чисел більше те, у якого більше сотень. 3. Якщо у трицифрових чисел сотень порівну, то далі слід порівнювати кількість десятків, потім – кількість одиниць. 317 < 371, бо 3 сот. = […]...

  40. Письмове додавання та віднімання багатоцифрових чисел Розділ IV Арифметичні дії з багатоцифровими числами Письмове додавання та віднімання багатоцифрових чисел 673. Математична розминка. Обчисли частку, одержану відділення числа 824 на число, що дорівнює кількості його десятків. Обчисли частку, одержану відділення числа 60 300 на число, що дорівнює кількості його сотень. Обчисли частку, одержану від ділення числа 8100 на число, що дорівнює сумі […]...

Ви зараз читаєте: Віднімання натуральних чисел
«
»