Вирази зі змінними. Цілі раціональні вирази. Числове значення виразу
Розділ 1. ЦІЛІ ВИРАЗИ
& 1. Вирази зі змінними. Цілі раціональні вирази. Числове значення виразу
Числові вирази утворюють із чисел за допомогою знаків дій і дужок. Наприклад, числовими виразами є:
12 ∙ 3 – 9; 1,23; 5 
– ( 5,7 : 3 + 1 
) тощо.
Число, що є результатом виконання всіх дій у числовому виразі, називають значенням виразу.
Оскільки 12 ∙ 3 – 9 = 36 – 9 = 27, то число 27 є значенням числового виразу 12 ∙ 3 = 9.
Якщо числовий вираз містить дію, яку неможливо виконати, то кажуть, що вираз
5 : (8 : 2 – 4) не має смислу, бо 8 : 2 – 4 = 0 і наступну дію 5 : 0 виконати неможливо.
Окрім числових виразів у математиці зустрічаються вирази, що містять букви. Такі вирази ми називали буквеними.
Приклад 1. Нехай необхідно знайти площу прямокутника, довжина якого дорівнює 10 см, а ширина – b см.
За формулою площі прямокутника маємо: S = 10b. Якщо, наприклад, b – 3, то S = 30, а якщо b = 7, то S = 70. У виразі 106 буква b може набувати різних значень, тобто її значення можна змінювати. При цьому буде змінюватися і значення виразу 10 b. Оскільки значення b може змінюватися (набувати різних,
Наприклад, вирази 5 + а; 2(6 – 3х);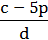 
виразами зі змінними.
Якщо у вираз зі змінними замість змінних підставимо певні числа, то одержимо числовий вираз. Його значення називають числовим значенням виразу для вибраних значень змінних.
Приклад 2. Знайти значення виразу:
1) (5 + b) : 4, якщо b = 0; -2; 2) a –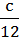 
, якщо а = 17, с = -5.
Р о з в’ я з а н н я.
1) Якщо b = 0, то (5 + b) : 4 = (5 + 0) : 4 = 1,25;
Якщо b = -2, то (5 + b) : 4 = (5 + (-2)) : 4 = 0,75.
2) Якщо а = 17, с = -5, то a – 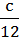= 17 – 
= 
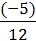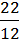= 1 
.
Вираз, який складається із чисел і змінних, сполучених знаками дій та дужок, називають раціональним виразом. Наприклад, раціональними є вирази:
2 а – m; p +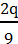 
; – 
(x – 9 + y); 5 +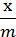 
; 
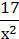– 3; a + b – 
.
Раціональний вираз, який не містить ділення на вираз зі змінною, називають цілим раціональним виразом. Якщо в раціональному виразі є ділення на вираз зі змінною, його називають дробовим раціональним виразом. Три перших з поданих вище виразів – цілі, а три останніх – дробові.
Вирази зі змінними використовують для запису формул.
Наприклад, s = vt – формула відстані; Р = 2(а + b) – формула периметра прямокутника; n = 2k (де k – ціле число) – формула парного числа; n = 2k + 1 (де k – ціле число) – формула непарного числа; n = 7k (де k – ціле число) – формула числа, кратного числу 7.
А ще раніше…
Поява букв і знаків арифметичних дій y математичних записах є результатом розвитку математичної науки. У своїх працях шукане невідоме число стародавні єгипетські вчені називали “хау” (у перекладі – “купа”), а знаки математичних дій взагалі не вживали, записуючи усе переважно словами. І хоча потреба у використанні знаків математичних дій виникла ще у Стародавньому Єгипті, з’явилися вони набагато пізніше. Замість знаків додавання і
Віднімання стародавні математики використовували малюнки або слова, що призводило до громіздких записів.
Знаки арифметичних дій стали зустрічатися в наукових працях математиків, починаючи з XV ст. На сьогодні відомо, ким і коли було запропоновано деякі математичні знаки для записів. Так, знаки “+” і”-” зустрічаються вперше у 1489 році в праці “Арифметика” Погана Відмана. професора Лейпцизького університету. Знак “х” для позначення дії множення введено англійським математиком Вільямом Оутредом у 1631 році. Для позначення дії ділення він використовував риску “/”. Дробову риску в математичних записах (для відокремлення чисельника дробу від його знаменника) уже в 1202 році використовував Леонардо Пізанський, відомий математик середньовічної Європи. Німецький математик, фізик і філософ Готфрід Вільгельм Лейбніц (1646-1716) запропонував використовувати у якості знака множення крапку (“∙”), а у якості знака ділення – двокрапку (“:”). Це відбулося у 1693 році та у 1684 році відповідно. Знак рівності (“-“) було введено в 1557 році Робертом Рекордом, математиком, який народився в Уельсі і довгий час був особистим лікарем королівської сім’ї Великої Британії.
Величезний внесок у розвиток алгебраїчної символіки зробив у XVI ст. видатний французький математик Франсуа Віст, якого називають “батьком” алгебри. Саме він став позначати буквами не тільки змінні, а й будь-які числа, зокрема коефіцієнти при змінних. Проте його символіка відрізнялася від сучасної.
Замість х, х2 і х3 Вієт писав відповідно букви N (Numerus – число), Q (Quadratus – квадрат) і С (Сubus – куб). Наприклад, рівняння х3 + 7×2 – 8х = 20 він записував так:
1C + 7Q – 8N aequ 20 (aequali – дорівнює).
Франсуа Віст (1540-1603)
Із чого утворюють числові вирази? Що називають значениям числового виразу? Із чого утворюють вирази зі змінними? Що називають числовим значенням виразу для вибраних значень змінних? Наведіть приклад числового виразу і виразу зі змінними. Який вираз називають цілим раціональним виразом?
1. (Усно) Які з наведених нижче виразів є числовими, а які – виразами зі змінними:
1) 5 + m2 – а;
2) (12 – 3) : 4;
3) 
;
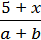4) (0 – 8) ∙ 5 – 13?
2. (Усно) Які з раціональних виразів є цілими, а які – дробовими:
1) 
;
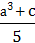2) 
;
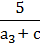3) m + 
;
4) m + 
?
3. Випишіть окремо: числові вирази; вирази зі змінними; цілі раціональні вирази; дробові раціональні вирази:
1) 5 + с;
2) (2 – 15) ∙ 4;
3) 
;
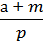4) q2 – 19;
5) 7 + 
;
6) 
ab;
7) 
;
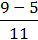8) 
.
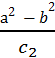4. Прочитайте словами вирази зі змінними:
1) х + 7;
2) m – а;
3) 5ab;
4) 5 : (с + 9).
5. Складіть і запишіть по два вирази:
1) зі змінною а;
2) зі змінними х і у.
6. Складіть і запишіть по три вирази:
1) зі змінною х;
2) зі змінними а і b.
7. (Усно) Які з даних числових виразів не мають смислу:
1) (5 – 6) : 7;
2) (10 – 2 ∙ 5) : 7;
3) 4 : (12 – 2 ∙ 6);
4) 
?
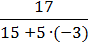8. Знайдіть значення виразу:
1) 5х – 3, якщо х = 1,8; де x = 2 
;
2) а2 + 3а, якщо а = -1; а = 0,8.
9. Знайдіть значення виразу:
1) 5m + 2n, якщо m = -1,3; n = 2 
;
2) а(2b – с), якщо а = 1,5; b = 3,2; с = -1,4.
10. Знайдіть значення виразу:
1) b2 – 4b, якщо b = -2; b = 0,5;
2) х2 – y2, якщо х = 5; у = -3; якщо х = 0,1; у = 0,2.
11. Запишіть у вигляді виразу:
1) суму чисел b і с;
2) добуток чисел 5m і n3;
3) квадрат суми чисел а і 9р;
4) різницю квадратів чисел 3d і 7r.
12. Запишіть у вигляді виразу:
1) різницю чисел р і 7;
2) частку чисел а + с і d;
3) суму числа а і добутку чисел m і n.
13. Заповніть у зошиті наступні таблиці:
M | 2 | 3 | -1 | 0 | -2 |
N | 1 | 2 | 0 | -5 | -3 |
2m – 3n |
X | -1 | 0 | 1 | 2 |
Х2 + 2 | ||||
Х2 + 2х |
14. Дізнайтеся прізвище видатного українського кардіохірурга. Для цього знайдіть значення виразу в першій таблиці і перенесіть букви, що відповідають знайденим значенням, у другу таблицю.
Х | -2 | -1 | 0 | 1 | 2 |
Х2 – 4х | |||||
Букви | О | А | В | М | С |
5 | -3 | 12 | -4 | 12 | 0 |
15. Порівняйте суму а + b з добутком ab, якщо:
1) а = 0, b = -2;
2) а = -3, b = 2.
16. Майстер за одну годину виготовляє х деталей, а його учень – у деталей. Скільки деталей вони виготовили разом, якщо майстер працював 8 год, а учень – 4 год?
17. (Усно) Нехай а дм – довжина прямокутника, b дм – його ширина. Що означають вирази:
1) ab;
2) 2(а + b);
3) 2а;
4) 
?
18. Ручка коштує х грн, олівець у грн (x > у). Що означають вирази:
1) х + у;
2) 3х + 4у;
3) х – у;
4) 
?
19. Запишіть у вигляді виразу час, який учень щоденно проводить у школі, якщо у нього а уроків по 45 хв, b перерв по 15 хв і с перерв по 10 хв. Обчисліть значення цього виразу, якщо а = 6; b = 2; с = 3.
20. Коли Марійка витягла зі своєї скарбнички всі монети, то виявилося, що там було х монет номіналом 10 коп., у монет номіналом 25 коп. і z монет номіналом 50 коп. Обчисліть, яку суму коштів назбирала Марійка, якщо х = 8; у = 5; z = 20.
21. При якому значенні змінної а значення виразу 5а – 8 дорівнює -13?
22. При якому значенні де значення виразів 3х – 4 і -2х + 7 рівні між собою?
23. Складіть формулу цілого числа, яке:
1) кратне числу 9;
2) при діленні на 5 дає в остачі 1.
24. При деяких значеннях а і b значення виразу а – b дорівнює 2,25. Якого значення при тих самих значеннях а і b набуває вираз:
1) 4(а – b);
2) b – а;
3) 
;
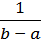4) 
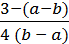
25. При деяких значеннях с і d значення виразу с – d дорівнює 
. Якого значення при тих самих значеннях с і d набуває вираз:
1) 7(с – d);
2) d – c;
3) 
;
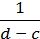4) 
?
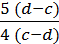26. Складіть вирази для обчислення площ фігур (мал. 1-3):
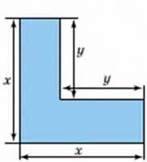
Мал. 1
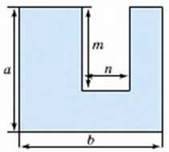
Мал. 2
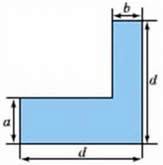
Мал. 3
Вправи для повторення
27. Обчисліть:
1) 132;
2) 73;
3) (-2,1)2;
4) (-1,1)3;
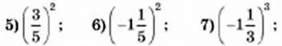
8) 0,23.
28. Якою цифрою закінчується значення виразу:
1) 1322; 2) 2713; 3) 20172; 4) 13152 – 1153?
29. Власна швидкість катера 26 км/год, а швидкість течії річки – 2 км/год. Знайдіть відстань між двома пристанями, якщо в одному напрямі катер проходить її на 30 хв швидше, ніж у зворотному.
Цікаві задачі для учнів неледачих
30. Чи існує таке значення х, для якого:
1) – х >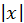 
;
2) х > ?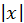
(1 votes, average: 5.00 out of 5)
Loading...