Головна ⇒ 📌Довідник с фізики ⇒ Висновки з перетворень Лоренца

Висновки з перетворень Лоренца

ФІЗИКА

Частина 4

ОПТИКА. СПЕЦІАЛЬНА ТЕОРІЯ ВІДНОСНОСТІ

Розділ 14 ШВИДКІСТЬ ПОШИРЕННЯ СВІТЛА. ОСНОВИ СПЕЦІАЛЬНОЇ ТЕОРІЇ ВІДНОСНОСТІ

14.6. Висновки з перетворень Лоренца

Слід зазначити, що у формули перетворень Лоренца (14.9) і (14.10) входять не довжини відрізків і не проміжки часу, а координати окремих подій. Наприклад, час t відлічується за годинником, який перебуває в стані спокою в системі К, а час t – за годинником, що не рухається в системі К’. Із перетворень Лоренца випливає чимало незвичайних з погляду класичної механіки

висновків.

1. Відносність одночасності. У класичній фізиці проміжок часу між будь-якими двома подіями не залежить від системи відліку. Це знайшло своє відображення у перетвореннях Галілея для часу: t = t’. Тоді проміжок часу

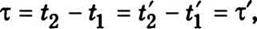
Де ti і ti’ – моменти часу, що відповідають здійсненню першої (t1 і t1′) і другої (t2 і t2′) подій, виміряних відповідно в нерухомій і рухомій інерціальних системах відліку. Якщо τ = τ’, то дві події одночасні в деякій інерціальній системі відліку (τ = 0) мають бути одночасними і в усіх інших інерціальних системах відліку (τ’ = 0). Отже, виходячи з перетворень

Галілея, одночасність абсолютна. З перетворень Лоренца випливає відносність одночасності: події, одночасні в одній інерціальній системі відліку, не обов’язково є одночасними в інших інерціальних системах, які рухаються відносно першої прямолінійно і рівномірно. Справді, нехай у системі К дві події сталися в момент часу t1 і t2, a місце їх визначається координатами х1 і х2. У системі К’ цим подіям відповідатимуть моменти часу t1′ і t2′ і координати х1′ і х2′. Припустімо, що в системі К події відбуваються одночасно, тобто t1 = t2 = t. Тоді, виходячи з перетворень Лоренцо (14.9), можна записати

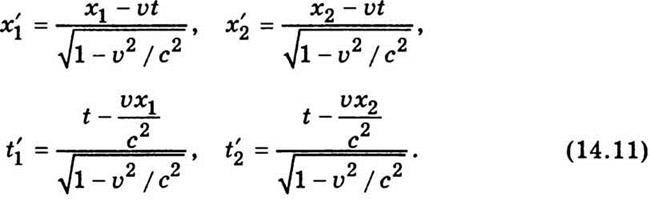
Із формул (14.11) випливає, що коли одночасні події в системі К відбуваються в одній точці простору (x1 = х2), вони збігатимуться в просторі (х1′ = х2′) і часі (t1′ = t2′) і в системі К’, а також у будь-якій іншій інерціальній системі, яка рухається відносно системи К. Проте якщо одночасні події в системі К просторово розділені (х1 ≠ x2) то в системі К’ вони неодночасні (t1′ ≠ t2′) І просторово розділені (х1′ ≠ х2′).

2. Сповільнення часу. Розглянемо процес, що відбувається в точці з координатою х’ нерухомій відносно системи К’. Позначимо тривалість цієї події за годинником системи К’ через τ’, причому τ’ = t2′ – t1′, де індекси 1 і 2 відповідають початку і кінцю процесу. Визначимо тривалість події τ = t2 – t1 у системі К. Відповідно до формул перетворення Лоренца (14.10) можна записати:

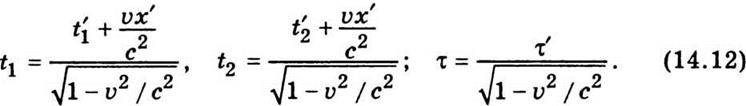
Отже, тривалість події, що відбувається в певній точці, мінімальна в тій інерціальній системі відліку, відносно якої ця точка є нерухомою. Одержаний результат можна сформулювати інакше, а саме: годинник, який рухається відносно інерціальної системи відліку, йде повільніше від годинника, що перебуває у стані спокою. Тому плинність часу в рухомій системі повільніша, ніж у нерухомій. Із співвідношення (14.12) видно, що сповільнення ходу годинника стає істотним лише при швидкостях υ, що наближаються до швидкості світла у вакуумі. Релятивістський ефект сповільнення плинності часу блискуче підтвердився в дослідах з μ-мезонами – нестабільними елементарними частинками, що входять до складу космічного випромінювання. Середній час життя нерухомого μ-мезона становить близько 2 ∙ 10-6 с. Здавалося б, що, рухаючись навіть зі швидкістю світла, μ-мезони можуть пройти шлях близько 600 м. Проте, як свідчать спостереження, ц-мезони виникають у космічному випромінюванні на висоті 20…30 км і багато з них досягає поверхні Землі. Це пояснюється тим, що 2 ∙ 10-6 с – власний час життя μ-мезона – час, виміряний за годинником, який би рухався разом з ним. Час, відрахований за годинником експериментатора на Землі, відповідно до співвідношення (14.12), набагато більший.

3. Формула лоренцового скорочення. Розглянемо стрижень, розташований уздовж осі х, який перебуває в стані спокою відносно системи К’. Тоді відносно системи К цей стрижень рухатиметься зі швидкістю υ. Порівняємо довжини стрижня у системах К і К’. У системі К’ відносно якої стрижень перебуває у стані спокою, визначення довжини стрижня зводиться до визначення координат х1′ і х2′ його кінців. Довжиною стрижня у системі К’ є l’ = х2′ – х1′.

У системі К, відносно якої стрижень рухається, справа ускладнюється тим, що треба визначити одночасно координати кінців стрижня x1 i х2. Тоді l = x2 – x1. Відповідно до формул перетворень Лоренца (14.9) маємо

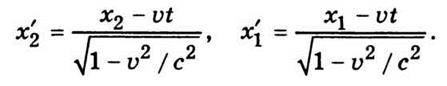
Звідси

Отже, в системі К, відносно якої стрижень рухається, довжина його менша, ніж у системі К’ відносно якої стрижень перебуває в стані спокою. Співвідношення (14.13) називають формулою ло – ренцового скорочення. Слід зауважити, що формули перетворень Лоренца втрачають свій зміст, коли υ = с, оскільки тоді в знаменнику з’являються нулі, а ділення на нуль, як відомо, неможливе. Це означає, що ніякі дві системи відліку не можуть мати відносну швидкість, яка дорівнювала б швидкості світла. Цей результат випливає також із формули лоренцового скорочення: тіло, що рухалося б зі швидкістю світла, мало б поздовжні розміри, які дорівнювали б нулю.

4. Закон додавання швидкостей. У класичній механіці, як відомо, швидкість тіла просто додається до швидкості системи відліку. Розглянемо це питання в релятивістській механіці й обмежимося одновимірним випадком. Нехай у двох системах відліку К і К’ вивчається рух тіла, яке переміщується прямолінійно і рівномірно паралельно осям х і х’ обох систем відліку (див. рис. 14.5). Нехай швидкість тіла, визначена в системі К, є u, а швидкість того самого тіла, визначена в системі К’ – u’. Швидкість системи К’ відносно системи К позначимо через υ. Унаслідок руху тіла його координати в системах К і К’ змінюються. Початкове положення тіла в системі К визначається координатами х1, t1, кінцеве – х2, t2. У системі К’ координати тіла відповідно дорівнюватимуть х1′, t1′ і х2′, t2′. Швидкість тіла визначається відношенням пройденого тілом шляху до відповідного проміжку часу. Тому для знаходження швидкості тіла в обох системах відліку треба різницю просторових координат обох подій поділити на різницю часових координат:

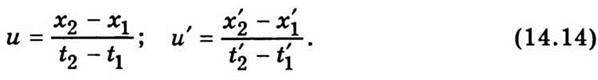
Із формул перетворень Лоренца дістанемо

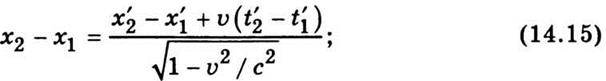
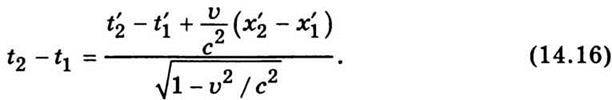
Поділимо відповідно праві і ліві частини цих рівностей:

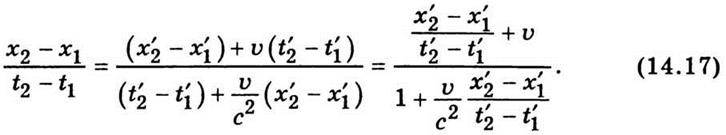
Отже, дістанемо релятивістську формулу додавання швидкостей

Розглянемо мислений експеримент. Нехай ракета рухається зі швидкістю світла (u’ = с) відносно системи К’, а сама система К’ також рухається відносно системи К зі швидкістю υ= = с. Якою буде швидкість ракети відносно нерухомої системи К? Щоб відповісти на це запитання, скористаємось релятивістським законом додавання швидкостей (14.18)

Цей результат пояснює і дослід Майкельсона. Один з основних висновків спеціальної теорії відносності полягає в тому, що жодне тіло не може рухатись зі швидкістю, більшою за швидкість світла у вакуумі. Справді, якщо швидкість тіла наближається до швидкості світла, то його об’єм унаслідок лоренцового скорочення (14.13) прагнутиме до нуля, а маса – до нескінченності.

Слід звернути увагу на те, що однаковою в усіх системах є лише швидкість світла у вакуумі. Швидкість світла в речовині в різних системах відліку різна. Значення с/n вона має в системі відліку, що пов’язана з середовищем, в якому поширюється світло. Якщо υ ” с, то формула (14.18) переходить у формулу додавання швидкостей класичної механіки.