Головна ⇒ 📌Довідник з геометрії ⇒ Властивості подібних фігур

Властивості подібних фігур

Геометрія

Подібність фігур

Теорема. Коли фігура 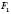подібна фігурі 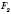, а фігура 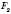– фігурі 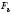, то фігури 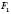і 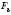Подібні.
Із властивостей перетворення подібності випливає, що у подібних фігур відповідні кути рівні, а відповідні відрізки пропорційні. Наприклад, у подібних трикутниках ABC і :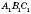

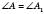
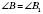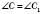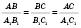class=""/>;

;

Ознаки подібності трикутників

Теорема 1. Якщо два кути одного трикутника відповідно дорівнюють двом кутам другого трикутника, то такі трикутники подібні.
Теорема 2. Якщо дві сторони одного трикутника пропорційні двом сторонам другого трикутника і кути, утворені цими сторонами, рівні, то трикутники подібні.
Теорема 3. Якщо сторони одного трикутника пропорційні сторонам другого трикутника, то такі трикутники подібні.
Із цих теорем випливають факти, що є корисними для розв’язування задач.
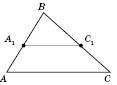
1. Пряма,

яка паралельна стороні трикутника і яка перетинає дві інші його сторони, відтинає від нього трикутник, подібний даному.
На рисунку

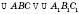2. У подібних трикутників відповідні елементи (висоти, медіани, бісектриси тощо) відносяться як відповідні сторони.
3. У подібних трикутників периметри відносяться як відповідні сторони.
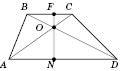
4. Якщо О – точка перетину діагоналей трапеції ABCD

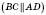, то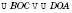

.
На рисунку в трапеції ABCD:

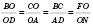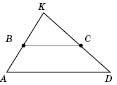
5. Якщо продовження бічих сторін трапеції ABCD

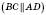перетинаються в точці K, то

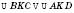(див. рисунок).

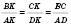Подібність прямокутних трикутників

Теорема 1. Якщо прямокутні трикутники мають рівний гострий кут, то вони подібні.
Теорема 2. Якщо два катети одного прямокутного трикутника пропорційні двом катетам другого прямокутного трикутника, то ці трикутники подібні.
Теорема 3. Якщо катет і гіпотенуза одного прямокутного трикутника пропорційні катету й гіпотенузі другого прямокутного трикутника, то такі трикутники подібні.
Теорема 4. Висота прямокутного трикутника, проведена з вершини прямого кута, розбиває трикутник на два прямокутні трикутники, подібні даному.
На рисунку .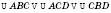

Із подібності прямокутних трикутників випливає таке.
1. Катет прямокутного трикутника є середнім пропорційним між гіпотенузою і проекцією цього катета на гіпотенузу:
; ,
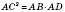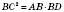або
; .
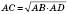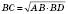2. Висота прямокутного трикутника, проведена з вершини прямого кута, є середнім пропорційним між проекціями катетів на гіпотенузу:
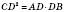, або .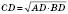
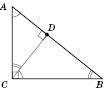
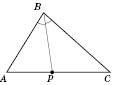
3. Властивість бісектриси трикутника:
бісектриса трикутника (довільного) поділяє протилежну сторону трикутника на відрізки, пропорційні двом іншим сторонам.
На рисунку у BP – бісектриса .
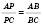, або .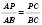

Подібність рівносторонніх і рівнобедрених трикутників

1. Усі рівносторонні трикутники подібні.
2. Якщо рівнобедрені трикутники мають рівні кути між бічними сторонами, то вони подібні.
3. Якщо рівнобедрені трикутники мають пропорційні основу й бічну сторону, то вони подібні.