Внутрішня енергія і теплоємність ідеального газу
ФІЗИКА
Частина 2 МОЛЕКУЛЯРНА ФІЗИКА І ТЕРМОДИНАМІКА
Розділ 4 ОСНОВИ МОЛЕКУЛЯРНО-КІНЕТИЧНОЇ ТЕОРІЇ ГАЗІВ
4.6. Внутрішня енергія і теплоємність ідеального газу
Оскільки молекули ідеального газу на відстані не взаємодіють, внутрішня енергія такого газу складається лише з кінетичних енергій окремих молекул. Тоді внутрішня енергія моля ідеального газу дорівнюватиме добутку числа Авогадро на середню кінетичну енергію однієї молекули:
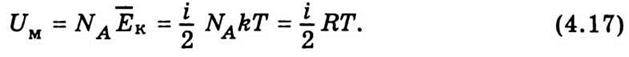
Внутрішня енергія довільної маси газу т дорівнює внутрішній
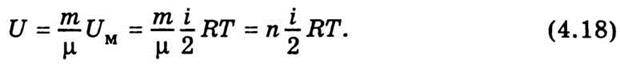
Теплоємністю називають фізичну величину, що визначається кількістю теплоти, яка потрібна для нагрівання певної маси на один градус. Якщо надана тілу кількість теплоти dQ підвищує його температуру на dТ, то його теплоємність
Теплоємність виражається у джоулях на кельвін (Дж/К). Розрізняють молярну та питому теплоємності. Теплоємність моля речовини позначають літерою С. Одиниця виміру її,- джоуль на моль-кельвін. Теплоємність одиниці маси речовини називають питомою теплоємністю, її позначають
Між молярною та питомою теплоємкостями речовини існує така залежність:
Де μ – молярна маса.
Теплоємність залежить від умов, за яких тіло нагрівається. Найбільший інтерес становить теплоємність для випадків, коли нагрівання здійснюється при сталому об’ємі або тиску. В першому випадку теплоємність називають теплоємністю при сталому об’ємі (СV), а в другому – теплоємністю при сталому тиску (Ср).
Якщо нагрівання відбувається при сталому об’ємі, тіло не здійснює роботи над зовнішніми тілами і, отже, вся теплота витрачається на приріст внутрішньої енергії тіла:
Звідси випливає, що теплоємність будь-якого тіла при сталому об’ємі
Отже, щоб дістати вираз для теплоємності моля ідеального газу при сталому об’ємі, треба здиференціювати за температурою вираз (4.17) для внутрішньої енергії газу. Виконавши диференціювання, дістанемо
Як випливає з цієї формули, теплоємність ідеального газу при сталому об’ємі залишається величиною сталою, що не залежить від параметрів стану газу, зокрема від температури.
Розглянемо один моль ідеального газу в двох різних станах, які мають однаковий об’єм, а за температурою відрізняються один від одного на один градус. Використавши вираз (4.17), дістанемо
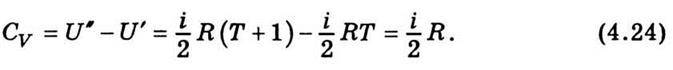
Визначимо молярну теплоємність газу при сталому тиску Ср = СV + ΔА, де ΔА – робота, яку виконує газ при розширенні, значення якої при р = const визначається за формулою ΔА = pΔV. Тоді
Де ΔV – зміна об’єму газу при нагріванні його на один градус при р = const. Для визначення ΔV використаємо рівняння стану для моля газу: pV = RT; V =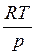 
. Звідси
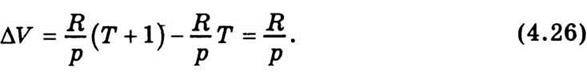
Підставивши значення ΔV у рівняння (4.25), дістанемо
Отже, робота, яку здійснює моль ідеального газу в разі підвищення його температури на один градус при сталому тиску, дорівнює універсальній газовій сталій.
З урахуванням формули (4.24) можна дістати для Ср такий вираз:
Поділивши (4.28) на (4.24), знайдемо характерне для кожного газу відношення Ср до СV:
Як випливає з (4.29), відношення теплоємкостей γ визначається числом ступенів вільності молекули.
(1 votes, average: 5.00 out of 5)
Loading...