Закон всесвітнього тяжіння
ФІЗИКА
Частина 1 МЕХАНІКА
Розділ 2 ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ
2.11. Закон всесвітнього тяжіння
Усі тіла в природі взаємно притягуються. Закон, що описує це притягання, відкрив І. Ньютон. Його називають законом всесвітнього тяжіння. За цим законом будь-які дві матеріальні точки притягуються одна до одної з силою, що прямо пропорційна добутку їхніх мас і обернено пропорційна квадрату відстані між ними:

Де G – коефіцієнт пропорційності, який називають гравітаційною сталою. Для визначення сили взаємодії
У разі довільних тіл, тобто тіл різної густини та форми, розв’язання такої задачі досить складне. Ця задача спрощується для однорідних куль і таких тіл, в яких масу умовно можна зосередити в одній точці. Для таких тіл можна застосувати закон всесвітнього тяжіння у вигляді (2.23).
Гравітаційні сили порівняно слабкі. Наприклад, вони значно слабкіші за електричні. Тому процеси
Гравітаційні сили стають відчутними для тіл великих мас і космічних тіл – планет, зірок тощо. Маса Сонця в 750 разів більша, ніж сумарна маса всіх планет Сонячної системи. Тому планети значно більше притягуються Сонцем, ніж одна одною. Наприклад, Місяць є природним супутником Землі й на нього найбільше впливає поле її тяжіння. Центр мас Сонячної системи зміщений від центра Сонця всього на 2,15R Сонця (радіус Сонця 695 989 км, відстань центра Сонця від центра мас Сонячної системи близько 1 486 000 км).
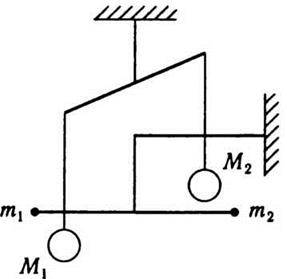
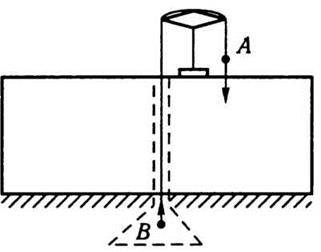
Рис. 2.5 Рис. 2.6
Для визначення сили гравітаційної взаємодії між тілами за законом Ньютона (2.23) треба знати гравітаційну сталу G. Вперше її експериментально визначив 1798 р. Г. Кавендіш. Він виміряв силу тяжіння між свинцевими кулями за допомогою крутильних терезів. Схематично основну частину приладу зображено на рис. 2.5. На одному стрижні підвішено дві масивні свинцеві кулі, на другому – дві невеликі свинцеві кульки. Всю установку вміщували в спеціальну камеру і захищали від коливань температури. Повертаючи стрижень з великими кулями, можна було спостерігати, що стрижень з малими кульками, який підвішено на нитці з відомими пружними властивостями, повертається на деякий кут назустріч важким кулям. За кутом закручування підвісу Г. Кавендіш підраховував сумарну силу притягання 2F між кулями М1 і m1 та М2 і m2. Відстань між центрами куль точно вимірювалась. Визначена Г. Кавендішем величина G відрізнялася лише на 1 % від тієї, яку дістали в наступних дослідах.
У 1898 р. Ріхарц до 100-річчя досліду Г. Кавендіша за ідеєю Ф. Жоллі визначив гравітаційну сталу іншим способом. Схему досліду Ріхарца подано на рис. 2.6. До кінця коромисла терезів підвішено дві кульки А і В, що мають однакові маси (з урахуванням підвісу). Свинцева плита масою 100 т своїм тяжінням збільшує вагу кульки А і зменшує вагу кульки В. Тому терези відхиляються від положення рівноваги. За відхиленням коромисла терезів можна судити про силу тяжіння між кулями й свинцевою плитою. Цей спосіб визначення G вважається найбільш точним. Установлено, що
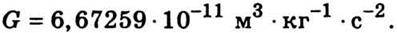
Використовуючи закон всесвітнього тяжіння (2.23), можна знайти залежність прискорення вільного падіння від висоти над поверхнею Землі. Справді, вага тіла зв’язана з його масою співвідношенням

Якщо нехтувати впливом добового обертання Землі, то за законом тяжіння вага тіла визначається за формулою

Де М3 – маса Землі; m – маса тіла; r – відстань тіла від центра Землі, що дорівнює радіусу Землі (R3 = 6 378 164 м), якщо тіло лежить на її поверхні. З формули (2.25) видно, що вага тіла зменшується з віддаленням тіла від земної поверхні. Оскільки маса тіла залишається сталою, то ця закономірність зумовлена характером поведінки прискорення вільного падіння від висоти. Якщо прирівняти співвідношення (2.24) і (2.25), то дістанемо аналітичний вираз цієї залежності

Де R3 – радіус Землі.
