Головна ⇒ 📌Плани-конспекти уроків по математиці ⇒ Аналіз тематичного опитування. Поняття про швидкість. Задачі на знаходження швидкості руху (№№ 490-499)

Аналіз тематичного опитування. Поняття про швидкість. Задачі на знаходження швидкості руху (№№ 490-499)

Тема. Аналіз тематичного опитування. Поняття про швидкість. Задачі на знаходження швидкості руху (№№ 490-499).

Мета. Провести аналіз тематичного опитування; з’ясувати типові помилки; організувати роботу над помилками; ознайомити учнів з поняттям “швидкість руху”, простими і складеними задачами на знаходження швидкості.

Обладнання. Таблиця “Швидкість. Час. Відстань”; схеми задач.

Зміст уроку

1. Аналіз тематичного опитування.

1. Загальна характеристика результатів тематичного опитування.

2. Аналіз помилок та

виконання відповідних завдань.

А) Проаналізувати типові помилки учнів.

Б) Колективне розв’язування завдань, аналогічних тим, у яких були допущені помилки.

В) Вправи для учнів, які успішно впоралися із завданнями тематичного опитування.

Робота № 12 (с. 7) із посібника М. В. Богдановича “Завдання для самостійної роботи. Математика. 4 клас.” – Тернопіль, 2012.

ІІ. Вивчення нового матеріалу.

1. Робота над вправою № 490.

2. Бесіда.

– Відомо, що учень пробіг 50 м за 10 с. Скільки метрів учень пробігав за одну секунду, якщо щосекунди він пробігав однакову кількість метрів?

class=""/>

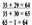
Учні розглядають схему задачі і роблять висновок: щоб відповісти на запитання задачі, треба 50 : 10 = 5 (м).

Отже, якщо за 1 с учень пробігає 5 м, то говорять, що він рухається зі швидкістю 5 м за секунду. Це записують так: 5 м/с.

Висновок. Щоб знайти швидкість, треба відстань поділити на час.

– З поняттям швидкості ми зустрічаємося часто: “тролейбус рухався повільно”, “літак рухався з надзвуковою швидкістю”, “друга космічна швидкість”, “швидкість променя світла” тощо.

Швидкості вимірюють у різних одиницях. Наприклад: 3 м/с; 10 м/хв.; 120 км/год. Ці одиниці швидкості можна перетворювати. Так, 5 м/с – це те саме, що 5 • 60 м/хв., тобто 300 м/хв.

3. Первинне закріплення.

А) Виконання завдання № 491.

Б) Робота з таблицею.

Рухомий об’єкт	Швидкість	Час	Відстань
Пішохід	5 км/год	3 год	15 км
Велосипедист	?	2 год	26 км
Автомобіль	?	4 год	280 км

За даними таблиці учні складають прості задачі на знаходження швидкості і розв’язують їх.

В) Самостійне виконання завдання № 492.

Г) Розв’язування задачі № 493 за поданим планом.

– Що треба знати, щоб відповісти на перше запитання задачі (на друге запитання)?

– Чи відомі ці числа?

– Чому дорівнює відстань, яку проїхав велосипедист? (72 км)

– Скільки часу він був у дорозі? (6 год)

– Як визначити швидкість велосипедиста? (Треба відстань поділити на час, тобто: 72: 6.)

– Як визначити швидкість мотоцикліста? (Треба 100 : 2 = 50 (км/год).)

– Чи можемо тепер відповісти на третє запитання плану? Чому?

– Що для цього потрібно зробити? (Від швидкості мотоцикліста відняти швидкість велосипедиста.)

(Розв’язання: 100 : 2 – 72 : 6 = 38 (км/год).)

Г) Розв’язування задачі № 494.

На дошці – ілюстрація до задачі.

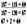
– Яку відстань пробіг хлопчик туди і назад?

– Скільки часу хлопчик біг туди і назад?

– З якою швидкістю біг хлопчик?

– Запишіть розв’язання задачі виразом. (400 • 2 : 4 = 200 (м/хв).)

Д) Розв’язування задачі № 495.

Учні з високим та достатнім рівнем знань працюють самостійно, решта – під керівництвом учителя.

(Розв’язання: 320 : 4 : 10 = 8 (км/с).)

Фізкультхвилинка.

III. Розвиток математичних знань.

1. Усне виконання вправи № 496 (1).

2. Самостійна робота № 496 (2, 3).

2) 20 грн 8 к. – 59 к. = 19 грн 49 к.

12 грн 70 к. – 8 грн 7 к. = 4 грн 63 к.

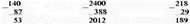
3) 30 грн 60 к. : 3 = 10 грн 20 к.

Учні звіряють відповіді із записаними на дошці.

3. Цікаві задачі.

– “Муха і мураха”.

Муха і мураха пішли пішки віт підлоги до стелі і назад. Муха віт підлоги до стелі рухалася вдвічі повільніше, ніж мураха, зате зворотний шлях вона подолала вдвічі швидше, ніж мураха. Мураха увесь час йшла з однаковою швидкістю. Хто раніше закінчив подорож?

(Розв’язання. Поки муха шила від підлоги до стелі, мураха встигла пройти вдвічі більшу відстань (адже вона рухалася вдвічі швидше за муху), тобто дійти від підлоги до стелі і назад. Мураха закінчила подорож набагато раніше, ніж муха: коли вона спустилася на підлогу, муха саме знаходилася на стелі.)

– “Винахідливий турист”.

Турист вирішив подорожувати з одного міста в інше, скориставшись попутним транспортом. Першу половину шляху він проїхав на машині, витративши у 10 разів менше часу, ніж якби йшов пішки. Однак другу половину шляху турист рухався на волах – удвічі повільніше, ніж якби йшов пішки. Чи швидше він здолав увесь шлях, ідучи таким чином, ніж якби пройшов його пішки?

(Розв’язання. На другу половину шляху турист витратив стільки часу, скільки потрібно було б, щоб подолати шлях пішки. Отже, він не заощадив час, а навпаки, витратив його більше на стільки, скільки зайняла поїздка на машині.)

– Задача № 497*. (Відповідь: 18 км/год.)

IV. Підсумок уроку.

– Відгадайте загадку.

Долає шлях вона за певний час, то змагаючись з будь-ким із нас, то вітер обганяючи, то хмарку здоганяючи.

Є вона і в кожного із нас, і в машини, літака чи черв’яка, у ракети, пароплава, і в жука. (Швидкість).

– Як знайти швидкість?

– В яких одиницях вимірюються швидкості?

V. Домашнє завдання.

№№ 498, 499 (с. 80): правило на с. 79.