ЦІЛІ ЧИСЛА. РАЦІОНАЛЬНІ ЧИСЛА
Розділ 4 РАЦІОНАЛЬНІ ЧИСЛА ТА ДІЇ З НИМИ
§ 24. ЦІЛІ ЧИСЛА. РАЦІОНАЛЬНІ ЧИСЛА
У п’ятому класі ви вивчали натуральні числа. Це числа, які використовують для лічби: 1; 2; 3; 4; … . Усі натуральні числа утворюють множину натуральних чисел. Цю множину позначають буквою N. Множина N має нескінченно багато елементів, оскільки натуральних чисел нескінченно багато.
Коротко це записують так: N=(1; 2; 3; 4;…).
Окрім множини натуральних чисел є й інші числові множини.
Натуральні числа, протилежні їм числа і число нуль утворюють множину цілих
Коротко це записують так:
Z = (… – 3; – 2; – 1; 0; 1; 2; 3; …).
Яким би не було натуральне число, воно є елементом множини цілих чисел. Проте не кожне ціле число є елементом множини натуральних чисел. Справді, будь-яке від’ємне число, яке є протилежним до натурального числа, є елементом множини цілих чисел. Але таке число не є натуральним. Співвідношення між цілими і натуральними числами показано на малюнку 114.
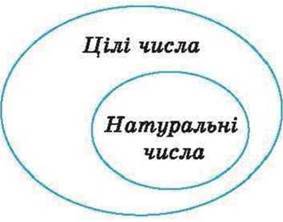
Мал. 114
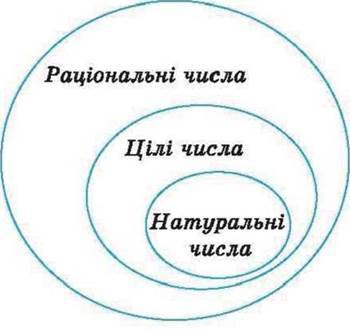
Мал.
? Чи можна вважати, що додатні цілі числа є натуральними числами? Так.
Крім цілих чисел ви знаете ще й дробові числа. Деякі з дробів позначають цілі числа, а деякі – ні. Наприклад, дріб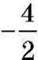 
дорівнює числу -2, яке є цілим. Вважають, що 
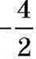і -2 – це різні записи одного числа. Про 
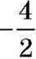ще кажуть, що це – число -2, яке записано у вигляді дробу. А от число 
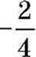навіть після скорочення дробу залишиться дробовим.
Зверніть увагу:
Не всі числа, записані у вигляді дробу, є дробовими.
Цілі числа та дробові числа утворюють множину раціональних чисел. Її позначають буквою Q. Множина раціональних чисел, як і множина цілих чисел, має нескінченно багато елементів. Співвідношення між натуральними, цілими і раціональними числами показано на малюнку 115.
Задача 1 Серед чисел 5,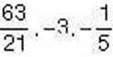 
Укажіть:
1) натуральні; 2) цілі; 3) раціональні.
Розв’язання.
1. Натуральними є числа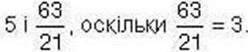 
2. Цілими є числа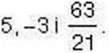 
3. Раціональними є числа 5,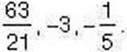 
Зверніть увагу:
– кожне натуральне число є і цілим числом, і раціональним числом;
– кожне ціле число є раціональним числом;
– не кожне раціональне число є цілим числом;
– не кожне раціональне число є натуральним числом.
Задача 2. На координатній прямій побудуйте точку, розміщену між точками А (2) і В (-4) і координата якої є: 1) від’ємним цілим числом; 2)додатним раціональним числом. Розв’язання. Побудуємо координатну пряму і позначимо на ній точки А і В (мал. 116).
Мал. 116
1. Узагалі між точками А (2) і В (-4) знаходиться п’ять точок із цілими координатами;-3,-2,-1, 0,1. Шукана точка М, координата якої є від’ємним цілим числом, розміщена між точками В і О. Це, наприклад, точка М (-3).
2. Узагалі між точками А (2) і В (-4) знаходиться безліч точок із раціональними координатами. Шукана точка Р, координата якої є додатним раціональним числом, розміщена між точками О і А. Це, наприклад, точка Р (1,5).
Зверніть увагу:
Між двома числами на координатній прямій знаходиться нескінченна кількість раціональних чисел.
Дізнайтеся більше
Поняття “множина” – одне з первинних понять математики. Множину можна утворювати не лише із чисел, а й з будь-яких інших об’єктів. Наприклад, цукерки в коробці, приладдя в пеналі теж утворюють відповідні множини. Об’єкти, з яких складається множина, називають елементами множини. Для позначення множин зазвичай використовують великі латинські літери А, В, С… . Множину, яка не містить жодного елемента, називають порожньою множною. Для її позначення використовують спеціальний знак: 0.
ПРИГАДАЙТЕ ГОЛОВНЕ
1. Які числа відносять до натуральних?
2. Як позначають множину натуральних чисел?
3. Які числа відносять до цілих?
4. Як позначають множину цілих чисел?
5. Які числа утворюють множину раціональних чисел?
6. Як позначають множину раціональних чисел?
7. Яке ціле число не є від’ємним і не є натуральним?
8. Як пов’язані між собою натуральні, цілі та раціональні числа?
РОЗВ’ЯЖІТЬ ЗАДАЧІ
1045′. Назвіть чотири:
1) натуральні числа; 3) раціональні числа;
2) цілі числа; 4) дробові числа.
1046′. Чи є правильним твердження:
1) -11 – ціле число; 7) -9,4 – ціле число;
2) 5 – раціональне число; 8) 0 – раціональне число;
3) -11 – натуральне число; 9) -9,4 – раціональне число;
4) 5 – натуральне число; 10) 0 – ціле число;
5) -11 – раціональне число; 11) -9,4 – натуральне число;
6) 5 – ціле число; 12) 0 – натуральне число?
1047′. Чи права Іринка, стверджуючи, що:
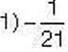– раціональне число;
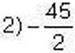– ціле число;
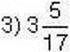– раціональне число;
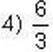– натуральне число?
1048°. Які з тверджень є правильними;
1) кожне натуральне число є цілим числом;
2) кожне натуральне число є раціональним числом;
3) кожне ціле число є раціональним числом?
1049°. Серед чисел 9; -8; 0; -4,6; 7,8; -475; 1143;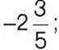 
оберіть:
1) натуральні числа; 4) цілі від’ємні числа;
2) цілі числа; 5) недодатні раціональні числа.
3) додатні числа;
1050°. Серед чисел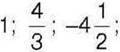 
-96,3; 0; -25; 283; 4,78; 11; 
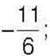56; -85; 
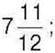2577 оберіть:
1) цілі числа; 4) дробові числа;
2) цілі додатні числа; 5) раціональні числа;
3) цілі від’ємні числа; 6) дробові від’ємні числа.
1051°. Серед чисел 534; -2,02; 0;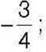 
33,01 оберіть:
1) натуральні числа; 2) цілі числа; 3) раціональні числа.
1052°. Наведіть приклад числа, яке:
1) є цілим, але не є натуральним;
2) є раціональним, але не є цілим і не є додатним.
1053°. Скільки цілих чисел і скільки натуральних чисел розміщується на координатній прямій між числами:
1)-12 і 12; 2)-62 і 62?
1054°. Скільки натуральних чисел і скільки цілих чисел можна позначити на координатній прямій між точками:
1 )А(12) і B(28); 2) С(-3,5) і D(-12,9); 3) М(-3,2) і N(10)? Назвіть ці числа.
1055°. Скільки цілих чисел можна позначити на координатній прямій між точками:
1) А(2) і В(2,5); 2) С(-5) і D(-12,9)?
1056°. Позначте на координатній прямій усі додатні цілі числа, які лежать ліворуч від числа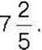 
1057°. Позначте на координатній прямій усі натуральні числа, які лежать ліворуч від числа 5, і числа, протилежні до них.
1058°. Запишіть усі цілі числа, модуль яких менший від числа:
1)3; 2)4,5; 3)1,25.
1059, Які з чисел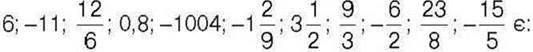 
1) цілими; 2) дробовими; 3) натуральними; 4) раціональними?
1060. Серед чисел, протилежних до чисел 15; -71; 0; – 1,1; 4,05;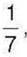 
оберіть:
1) натуральні числа; 3) цілі недодатні числа;
2) цілі числа; 4) раціональні числа,
1061. Які з чисел-3; 1230;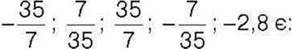 
1) цілими, але не натуральними;
2) дробовими, але не додатними;
3) раціональними, але не цілими?
1062. Знайдіть цілі числа, модуль яких знаходиться між числами:
1) 12 і 15; 3) -10 і 1; 5) 58,6 і 59,1;
2)-2 і 2; 4) 19 і 22;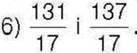 
1063. Чи є правильною рівність:
1) |а| = – а, якщо а – раціональне число;
2) |а| = а, якщо а – натуральне число;
3) |x| =-х, якщо х – ціле число;
4) |х| =-х, якщо х – натуральне є число?
1064. Чи є правильною рівність:
1) |а| = а, якщо а – раціональне число;
2) |х| = х, якщо х – ціле число?
1065. Укажіть такі цілі значення а, за яких між числами – а і а на координатній прямій розміщується тільки одне ціле число.
1066*. Чи існує таке значення а, за якого між числами -2а і а на координатній прямій: 1) лежить рівно сто цілих чисел; 2) не лежить жодного числа? Наведіть приклад.
1067*. Для яких натуральних чисел х і у справджується рівність: |x| +|у| =6?
1068*. Для яких цілих чисел х і у справджується рівність: |х| + |у|=8?
1069. Чи може існувати клас, у якому половина учнів вивчає тільки іспанську мову, чверть учнів – тільки німецьку мову, сьома частина учнів – тільки французьку мову, крім того, є ще три учні, які вивчають тільки китайську мову?
1070. Чи може існувати клас, у якому третина учнів грає тільки у футбол, чверть учні в-тільки у баскетбол, восьма части на учнів-тільки у теніс, крім того, є ще п’ять учнів, які не займаються спортом?
ЗАДАЧІ НА ПОВТОРЕННЯ
1071. Порівняйте значення числових виразів:
1)400094-20 900 +6 і 401 543-11 267+ 190;
2) 300 005 – 23 000 + 5 і 3 230 005 : 5 + 2.
1072. Порівняйте числа:
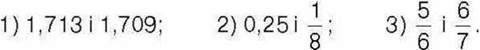
1073. Сашко задумав три числа. Сума цих чисел дорівнює 61,5. Сума першого і другого чисел дорівнює 40,2, а сума першого і третього становить 29,8. Які числа задумав Сашко?
(1 votes, average: 5.00 out of 5)
Loading...