МОДУЛЬ ЧИСЛА
Розділ 4 РАЦІОНАЛЬНІ ЧИСЛА ТА ДІЇ З НИМИ
§ 23. МОДУЛЬ ЧИСЛА
Позначимо на координатній прямій точки А (-6), В (-2) і С (2) (мал. 104). Яка точка розміщена найдалі від початку відліку О? Точка А, оскільки ОА = б од., а ОВ = ОС = 2 од.
Мал. 104
Порівнюючи відстані від точок А, В і С до початку відліку, ми шукали довжини відповідних відрізків ОА, ОВ і ОС. Кажуть: ми шукали модуль кожного із чисел – б, -2 і 2. Отже, модуль числа -6 дорівнює б, а модуль числа -2, так само, як і модуль числа 2, дорівнює 2.
Модуль числа позначають двома
Для чисел – б, -2 і 2 можемо записати: |-6| = 6, |-2| = 2, |2| = 2.
Зверніть увагу:
Модуль числа показує, на якій відстані від початку відліку знаходиться дане число на координатній прямій.
У цьому полягає геометричний зміст модуля числа. Звідси випливає, що модуль числа не може бути від’ємним числом. Фраза “модуль числа дорівнює -24” не має змісту.
? Чому дорівнює модуль числа 0? Модуль числа 0 дорівнює нулю: |0| = 0.
Розміщення точок В (-2) і С (2) (див. мал. 104) є особливим. Вони знаходяться на тій самій відстані від початку відліку О, але по різні
Запам’ятайте!
Два числа, що мають рівні модулі, але протилежні знаки, називаються протилежними числами.
Число 0 протилежне до самого себе.
? Як записати число, протилежне до даного числа? Для цього достатньо змінити знак даного числа на протилежний. Наприклад, для числа 5 протилежним є число -5, а для числа -5 протилежним є число +5 = 5.
Задача 1. Чому дорівнює модуль: 1) додатного числа; 2) від’ємного числа?
Розв’язання. 1. Нехай а – додатне число. На координатній прямій таке число розміщується праворуч від початку відліку О (мал. 105). Відстань від нього до початку відліку показує саме це число. Отже, модуль додатного числа а дорівнює цьому числу:
|а| = а, якщо а – додатне число.
Мал. 105
2. Нехай а – від’ємне число. На координатному промені таке число розміщується ліворуч від початку відліку О (мал. 106). Відстань від нього до початку відліку дорівнює відстані до точки О від протилежного до нього числа: – а. Це означає, що – а – додатне, якщо а – від’ємне. Отже, модуль від’ємного числа а дорівнює протилежному числу:
|а| = – а, якщо а – від’ємне число.
Мал. 10б
Запам’ятайте!
Властивості модуля числа
1. Модуль додатного числа дорівнює самому числу.
2. Модуль від’ємного числа дорівнює протилежному числу.
3. Модуль числа 0 дорівнює нулю.
Коротко записують:
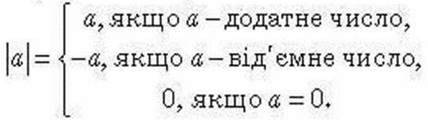
Задача 2. Знайдіть відстань між точками: 1)А (2) і В (-7); 2) А (2) і С (7); Z)D (-2) і В (-7).
Розв’язання. 1. На координатній прямій позначимо точки А (2) і В (-7) (мал. 107). З умови випливає, що ОА = 2 од., ОВ = 7 од. Оскільки точки А (2) і В (-7) розміщуються по різні сторони від точки О, то АВ = ОВ + ОА = 7 + 2 = 9 (од.). Отже, шукана відстань дорівнює сумі модулів координат даних точок.
Мал. 107
2. На координатній прямій позначимо точки А (2) і С (7) (мал. 108). Зумови випливає, щоОА=2 од., ОС-7од, Оскільки точки А (2) і С (7) розміщуються по одну сторону від точки О, то АС = ОС – ОА = 7 -2 = 5 (од.). Отже, шукана відстань дорівнює різниці більшого і меншого модулів координат даних точок.
Мал. 108
3. На координатній прямій позначимо точки D (-2) і В (-7) (мал. 109). Зумови випливає, що OD = 2од., ОВ = 7 од. Оскільки точки D (-2) і В (-7) розміщуються по одну сторону від точки О, то DB = ОВ – OD = 7-2 = 5 (од.). Отже, шукана відстань дорівнює різниці більшого і меншого модулів координат даних точок.
Мал. 109
Зверніть увагу:
Щоб знайти відстань між двома точками за їх координатами, треба:
– додати модулі координат, якщо координати мають різні знаки;
– від більшого модуля координати відняти менший модуль координати, якщо координати мають однакові знаки.
Дізнайтеся більше
Слово “модуль” – латинського походження: modulus – міра. Донедавна замість “модуль числа” говорили абсолютна величина. Так раніше називали “числа без знаків”, протиставляючи їм так звані “відносні числа” – числа зі знаками. Зараз терміни “відносні числа” й “абсолютна величина числа” вважають застарілими і їх не використовують.
ПРИГАДАЙТЕ ГОЛОВНЕ
1. Що таке модуль числа?
2. Яких значень може набувати модуль числа?
3. Чому дорівнює модуль числа 0 ?
4. Які числа називаються протилежними?
5. У чому полягає особливість розміщення протилежних чисел на координатній прямій?
6. Що можна сказати про модулі протилежних чисел?
7. Чому дорівнює модуль додатного числа?
8. Чому дорівнює модуль від’ємного числа?
РОЗВ’ЯЖІТЬ ЗАДАЧІ
983′. На якій відстані від початку відліку розміщується кожна точка (мал. 110)? Чому дорівнює модуль її координати?
Мал. 110
984′. Чи може модуль числа дорівнювати:
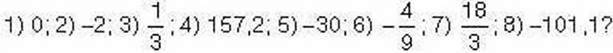
985′. Чи є протилежними числа:
1) 6 і -6; 2) 15 і 0; 3) 28 і 82; 4)-56 і 56; 5) 119 і-191?
986′. Чи правильно, що протилежним до числа-10 є число:
1)0; 2) -10; 3)10?
987°. На координатній прямій позначте точку з координатою:
1)3,5; 2)-7; 3)3; 4)-6.
Знайдіть модуль координати цієї точки.
988°. На координатній прямій позначте точку з координатою:
1) 0; 2) -5; 3) 8. Знайдіть модуль координати цієї точки.
989°. Модуль координати точки дорівнює:
1) 2; 2) 4; 3) 3.
Яку координату може мати точка?
990°. Модуль координати точки дорівнює:
1) 5; 2) 8.
Яку координату може мати точка?
991°. На координатній прямій побудуйте дві точки, у яких модуль координати дорівнює:
1) 5; 2) 4,5; 3) 2,5; 4) 1.
992°. На координатній прямій побудуйте дві точки, у яких модуль координати дорівнює:
1) 4; 2) 3,5; 3) 3; 4) 1,5.
993°. Яка відстань від точки А{а) до початку відліку на координатній прямій, якщо:
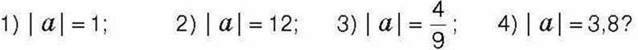
994°. Чи є протилежними числа:
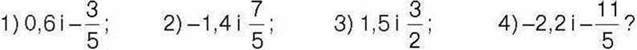
995°. Чи є протилежними числа:
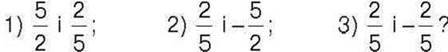
996°. Серед чисел 32;
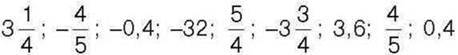
Оберіть пари протилежних чисел.
997°. Якими даними треба доповнити таблицю 6?
Таблиця 6
998°. Запишіть число, якщо протилежним до нього є число:
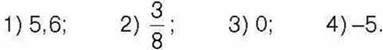
999°. Запишіть число, яке протилежне до числа:
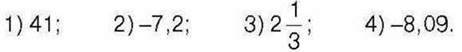
1000°. Знайдіть р, якщо:
1) – р = 9; 2)-р = -20; 3)-р = 0,4; 4)-р = 0.
1001°. Знайдіть – x, якщо:
1) x = 9,5; 2)х = -6; 3)х = -30; 4)х = 38.
1002°. Розв’яжіть рівняння:
1) – х = 34; 2)-х = 5; 3)-х = -65; 4)-х = -8.
1003°. Розв’яжіть рівняння:
1)-х = 28; 2)-х = 2; 3)-х = -86; 4)-х = -5.
1004°. Якими даними треба доповнити таблицю 7?
Таблиця 7
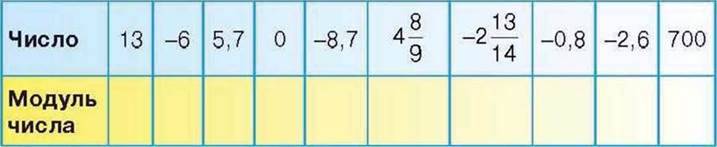
1005°. Знайдіть модуль числа:
1)7; 2)-8; 3)-42; 4) 0; 5)-1;
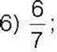7) 100; 8)-250;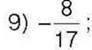 
10)0,01; 11)2,8;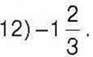 
1006°. Обчисліть:
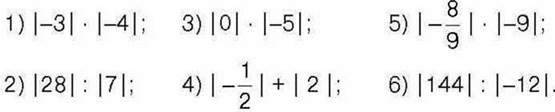
1007°. Знайдіть суму і добуток модулів чисел:
1)-0,6 i 3; 3)44 і-12; 5)-22 і 5;
2)-24 і 12; 4)-15 і -5; 6) -6 і 16.
1008°. Знайдіть суму і добуток модулів чисел:
1) 6 і -3; 2) 24 і-12; 3)-44 і 12; 4)-3 і-25.
1009°. Укажіть числа, модуль яких дорівнює:
1)18; 2)5,4; 3)12,1; 4)254;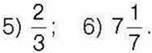 
1010°. Укажіть від’ємне число, модуль якого дорівнює:
1)24; 2)0,4; 3)14,25; 4)311.
1011°. Розв’яжіть рівняння:
1) |x| = 15; 3) |х|=4,5;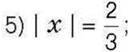 
1012°. Розв’яжіть рівняння:
1)|х| = 1; 2)|x| = 125; 3)|x|=7,8;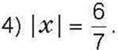 
1013°. Обчисліть значення виразу:
1) 5+ 8 ∙ | х |, якщо: а) x = 0,4; б) x = -0,4;
2) 17 – 16 ∙ | х |, якщо: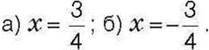 
1014°. Знайдіть число, протилежне до значення суми:
1) |15| + |38|; 3) |43|+ |-28|;
2) |-16|+ |11|; 4) | -101| + |-61.
1015 . Знайдіть число, протилежне до значення різниці:
1) |14| – |12|; 3) |61| – |-31|;
2)|-21| – |21|; 4) |-11| – | -11|.
1016°. Якими даними треба доповнити таблицю 8?
Таблиця 8
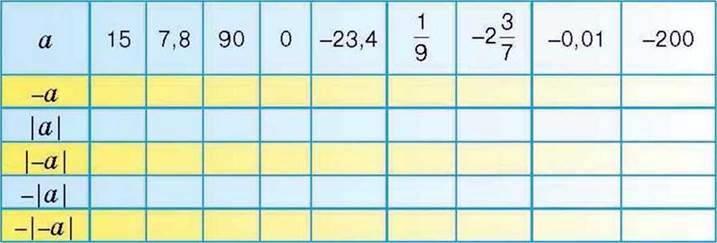
Яку закономірність ви помітили?
1017°. Порівняйте модулі чисел:
1) -41 і 41; 2)-2,5 і 2,5;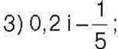 
4)-1,5 і 1,5.
1018°. Користуючись координатною прямою, обгрунтуйте, що: |а| = |-а|.
1019°. Знайдіть відстань між точками:
1) А(25) і B(23); 2) С(-2) і D(8); 3) М(-14) і N(-4).
1020. Визначте одиничний відрізок координатної прямої на малюнку 111, якщо модуль координати точки А дорівнює: 1) 3; 2) 2.
Мал. 111
1021. Визначте одиничний відрізок координатної прямої на малюнку 112, якщо модуль координати точки В дорівнює: 1) 4; 2) 6.
Мал. 112
1022. Користуючись координатною прямою, поясніть суть твердження:
1) число, протилежне до додатного числа, є від’ємним;
2) число, протилежне до від’ємного числа, є додатним.
1023. Знайдіть число, протилежне до числа, яке протилежне до числа:
1)36; 2)217; 3)-96; 4)-127.
1024. Чому дорівнює |а| + а, якщо – а = -5,002?
1025. Накресліть у зошиті та заповніть таблицю 9.
Таблиця 9
Яку закономірність ви помітили?
1026. Обчисліть:
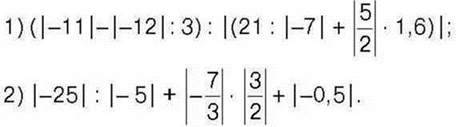
1027. Чи правильно, що:
1) протилежним до числа | -31 є число -3;
2) протилежним до числа 4 є число-|-4|?
1028. Чи існує таке число а, що: 1) | a | = -|а|; 2) |a| = -|а|? Якщо так, то наведіть приклад.
1029. Розв’яжіть рівняння:
1) |x|- 70 = 30; 4) |-х| = 54,9;
2) |х|+ 55 = 68; 5)|-х|=-4;
3) |х|-32 = 79; 6)-|х| =-12.
1030. Розв’яжіть рівняння:
1) |x| =4,2; 2) |-х| =-115; 3)|-x|=0; 4)11 + |х|=43.
1031. Знайдіть: 1)20%числа |-1001; 2) 75% числа |-250| + 112501.
1032. Знайдіть відстань між точками:
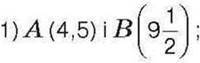
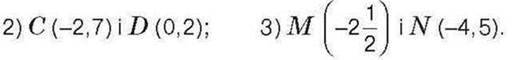
1033. У скільки разів відстань між точками А (-62) і М (-7) більша за відстань між точками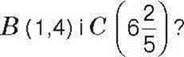 
1034*. За якого значення а число, що є значенням виразу 2а – 8, є протилежним до себе?
1035*. Розв’яжіть рівняння:
1) ||x|+2| =0; 3) |4-х| + 128 = 0;
2) ||х|-5| =0; 4) |-х| +3=125.
1036*. Розв’яжіть рівняння:
1) 3 ∙ |x| = |х| + 8; 2)2 -|х|-6 = |-х|;3)4-|х-2|= |2-х|.
1037*. На координатній прямій (мал. 113) позначено точки, які відповідають числам 1 і а. Перемалюйте малюнок у зошит і позначте точки, які відповідають числам |а|, 2 | а|.
Мал. 113
1038*. Знайдіть відстань між точками:
1)А(|а – 11 + 4) i В (|-а+ 1|);
2) А (-|а|) і В (|2а|), якщо відстань між точками М(а) і N(-5a) дорівнює 6 і а – додатне число.
1039*. Спростіть вираз:
|а| + |а + 2| – 2, якщо а – додатне число.
ЗАСТОСУЙТЕ НА ПРАКТИЦІ
1040. Із пункту А в протилежних напрямках виїхали два автомобілі. Перший вирушив праворуч від пункту А і ‘їхав зі швидкістю 60 км/год. Другий за 2 год проїхав 100 км ліворуч. Якою буде відстань між автомобілями через 2 год після початку руху?
1041. Із пункту А в протилежних напрямках виїхали два велосипедисти. Перший із них проїхав 15 км ліворуч від пункту А. Другий проїхав 23 км праворуч, але потім повернувся на 5 км назад. Який велосипедист опинився на меншій відстані від пункту А?
ЗАДАЧІ НА ПОВТОРЕННЯ
1042. Назвіть натуральні числа, які менші від 23 і більші за 15.
1043. Назвіть найбільше натуральне число, яке менше від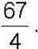 
1044. Виконайте дії:
1)217 м 7 дм 6 см + 95 м 34 см;
2)734 кг 886 г-115 кг 978 г;
3) 1 доба 23 год 56 хв + 4 доби 1 год 24 хв;
4) 4 доби 6 год 15 хв 45 с – 2 доби 23 год 54 хв 20 с.
(1 votes, average: 5.00 out of 5)
Loading...