Дифракція Фраунгофера
ФІЗИКА
Частина 4
ОПТИКА. СПЕЦІАЛЬНА ТЕОРІЯ ВІДНОСНОСТІ
Розділ 12 ХВИЛЬОВІ ВЛАСТИВОСТІ СВІТЛА
12.6. Дифракція Фраунгофера
Дифракція Фраунгофера спостерігається на нескінченності, тобто в паралельних променях. Часто для зручності спостереження використовують збиральну лінзу і дістають дифракційну картину у фокальній площині лінзи L (рис. 12.13). Дифраговані під певним кутом φ світлові пучки даватимуть зображення отвору АВ у фокальній площині лінзи L. Вважатимемо, що падаючі промені паралельні. Оскільки для кожної точки спостереження
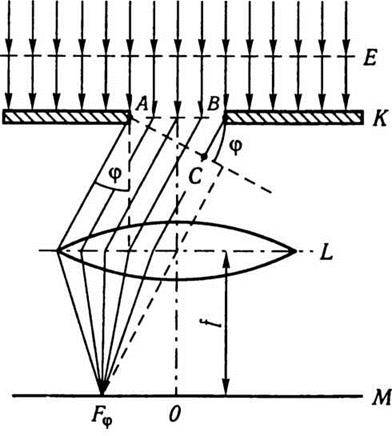
Рис. 12.13
Врахуємо, що внаслідок дифракції світлові промені від щілини поширюються не лише в початковому напрямі, а й під різними кутами φ до цього напряму. Всі промені, що падають на лінзу L під кутом φ до її оптичної осі, збиратимуться в точці (лінії) Fφ, яка розташована у фокальній площині лінзи L. Різниця оптичного ходу хвиль Δ між крайніми променями, що йдуть від щілини в цьому напрямі, буде

Щілину АВ можна розбити на зони Френеля. Ці зони матимуть вигляд однакових за шириною смуг, паралельних краям щілини. Оскільки для всіх таких зон кути між нормаллю до зони і напрямом дифрагованого променя виявляються однаковими, то всі вони однаково випромінюють світло в заданому напрямі. Амплітуда результуючих коливань, що приходять у точку спостереження від кожної пари сусідніх зон, дорівнює нулю, оскільки вони збуджують коливання з однаковими амплітудами і протилежними фазами в точці спостереження. Отже, результуюча амплітуда в точці Fφ визначатиметься числом зон Френеля, на які розбито щілину для кута дифракції φ. Якщо число зон для цієї точки спостереження парне, то в ній спостерігатиметься дифракційний мінімум:
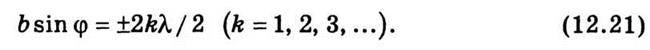
Знак мінус відповідає променям, які поширюються від щілини під кутом φ і збираються в точці (лінії), симетричній Fφ відносно головного фокуса 0. Якщо число зон непарне, то спостерігатиметься дифракційний максимум, що відповідає дії однієї зони Френеля:
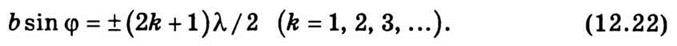
Число k називають порядком дифракційного максимуму (мінімуму). Отже, дифракційна картина, що утворюється від однієї щілини при освітленні її монохроматичним світлом, має вигляд світлих і темних смуг, які змінюють одна одну і розташовані симетрично по обидва боки від центральної світлої смуги. Яскравість світлих смуг швидко зменшується при віддаленні від центральної смуги. Якщо щілину освітлювати немонохроматичним світлом (білим), то характер дифракційної картини змінюється: центральна смуга залишається білою і лише по краях буде забарвленою, а всі максимуми, починаючи з максимуму першого порядку, розкладатимуться в спектр. У цьому разі повного затемнення не спостерігається в жодній точці екрана. Це пов’язано з тим, що максимуми і мінімуми світла для різних довжин хвиль перекриваються.
Важливе значення має дифракція Фраунгофера на багатьох паралельних однакових щілинах, розміщених в одній площині на однакових відстанях одна від одної. Таку систему щілин називають дифракційною решіткою. Дифракційні решітки використовують у спектроскопії для розкладання світла у спектр замість призми. Властивість решіток розкладати світло в спектр грунтується на тому, що положення дифракційних максимумів одного порядку для різних довжин хвиль неоднакове. Спектр, утворений за допомогою решітки, називають дифракційним, на відміну від спектра, що дає призма і який називають призматичним. Найпростіша дифракційна решітка – це пластинка, на якій чергуються вузькі прозорі й непрозорі смуги, паралельні між собою. Таку решітку можна виготовити, надряпавши на склі алмазом ряд штрихів. Можна виготовити також решітку, якщо нанести подряпини на поверхню металевого дзеркала. Таку решітку називають відбивною. Суму ширини прозорої (відбивної) і непрозорої (розсіювальної) смуг називають періодом решітки d.
При освітленні решітки монохроматичним світлом дифракційна картина, що спостерігається на екрані, розташованому в фокальній площині лінзи, складніша, ніж у випадку однієї щілини. Це пов’язано з тим, що у дифракційних решітках спостерігається не тільки взаємна інтерференція променів, які поширюються від однієї щілини, а й інтерференція променів, що приходять в точку спостереження від різних щілин. Це приводить до того, що поряд з так званими головними максимумами, які визначаються умовою

Де m = 0,1,2, … – порядок головного максимуму; d – період решітки, і головними мінімумами, які визначаються співвідношенням

Де k = 1,2,…; b – ширина однієї щілини, виникають дуже слабкі побічні максимуми, розділені додатковими мінімумами. Число побічних максимумів і додаткових мінімумів, що містяться між двома сусідніми головними максимумами, залежить від кількості щілин у решітці. Головні максимуми, що відповідають кутам φ, для яких одночасно виконуються співвідношення (12.23) і (12.24), не спостерігаються. Так, якщо d = 2b, то парних максимумів (m = 2, 4, 6 і т. д.) немає.
Дифракційні решітки широко застосовують на практиці, оскільки загальна кількість енергії, що проходить крізь решітку, пропорційна кількості щілин. Інтенсивність головних максимумів пропорційна квадрату кількості щілин. Отже, зі збільшенням кількості щілин енергія, що потрапляє в головні максимуми, зростає швидше, ніж загальний потік енергії, тобто зі збільшенням кількості щілин все більше енергії, що проходить, припадає на головні максимуми. Ці загальні енергетичні міркування приводять до висновку, що дифракційна картина зі збільшенням кількості щілин стає більш виразною. Найпростішим методом збільшення кількості щілин було б збільшення розмірів решітки. Проте практично такий метод малопридатний, тому збільшують кількість щілин на 1 мм, зменшуючи їхню ширину. В кращих сучасних решітках наносять до 1200 штрихів на 1 мм. Період такої решітки становить близько 800 нм. Великих успіхів у виготовленні перших дифракційних решіток досяг А. Майкельсон. У 1905 р. він виготовив решітку розміром 15 см, на яку було нанесено 110 000 штрихів. Через десять років А. Майкельсон виготовив дифракційну решітку розміром 20 см, а потім 24 см, яка є найбільшою з усіх виготовлених будь-коли дифракційних решіток. На неї нанесено 117 000 штрихів, що є значним досягненням у техніці експерименту.