Ділення раціональних чисел
Урок № 93
Тема. Ділення раціональних чисел
Мета: підготувати учнів до виконання тематичної контрольної роботи.
Тип уроку: систематизація та корекція знань.
Хід уроку
@ Оскільки цей урок є логічним завершенням попередньої роботи, схема його може бути такою самою, як і попереднього. Єдина відмінність – змістом навчального матеріалу є тема “Ділення раціональних чисел”.
І. Перевірка домашнього завдання
Спочатку обговорюємо труднощі, що, можливо, виникли під час виконання домашнього завдання (див. урок № 96).
Усні
1. Обчисліть:
А) |
| Б) |
|
2. Назвіть подібні доданки в сумі та їх коефіцієнти:
1) -2,4х + 4,3х + 8,2 – 8,2х;
2) 3 У – 3
У – 3 Х – 3
Х – 3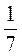 У + 3
У + 3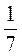 Х;
Х;
3) 4,5a – 4,5b + 10a – 10b;
4) 100a + 101b – 200a – 202b.
Зведіть подібні доданки.
3. Обчисліть значення виразу найзручнішим способом:
А) -25 – 106 – (-4);
Б) -4 – (-0,81) – 25;
В) 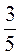 – (-8) –
– (-8) – 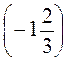 ;
;
Г)
Д) -1,23 – (-4) – (-5) – (-5);
Є) 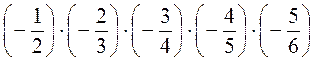
4. Дайте відповідь на запитання та наведіть приклади:
А) Яка кількість від’ємних множників повинна бути в добутку, щоб він виражався додатним числом? від’ємним числом?
Б) За якої умови добуток кількох множників дорівнює 0?
В) Як зміниться добуток декількох чисел, якщо його помножити на (-1)?
II. Систематизація знань
Проводиться в ігровій формі (див. попередній урок).
III. Відтворення, вдосконалення та корекція вмінь
@ На цьому уроці ми повторюємо та систематизуємо досвід, набутий у ході вивчення теми “Ділення раціональних чисел”, але насправді ми систематизуємо знання про виконання всіх інших арифметичних дій у комплексі з діленням. Тому й завдання, відібрані на урок, є в основному “комплексними”, тобто вимагають від учнів, окрім знань алгоритмів виконання арифметичних дій, ще й знання правил встановлення порядку виконання дій та правил, що виражають залежність між компонентами арифметичних дій.
1. 1) Виконайте ділення:
А) -124 : 31;
Б) -33,77 : (-11);
В) 53,4 : (-15);
Г) 1,242 : (-0,27);
Д) –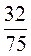 :
: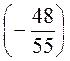 ;
;
Є) -1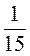 : 4
: 4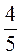 .
.
2) Виконайте дії:
А) 3,2 – (-6) – 7,8 : (8,8 – 10,1);
Б) (-31,7 : 63,4 – 23,4: (-1,17)) – (-2,4);
В) (-1,2 + 4,32 : (-1,8)) : (-0,001) – (-0,3).
3) Знайдіть значення виразу:
А)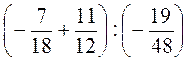 ; б)
; б)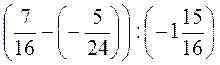 ; в)
; в)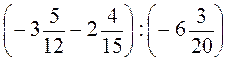 ; г)
; г) 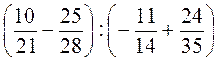 ; д)
; д) 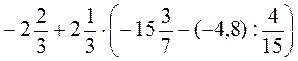 ;
;
2. 1) Усно розв’яжіть рівняння:
А) 5,2 : х = 5,2; x – 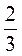 = -1; х : 5,72 = 0;
= -1; х : 5,72 = 0;
Б) -4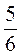 : х = 4
: х = 4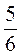 ; х :
; х : 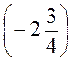 = -1; х :
= -1; х : 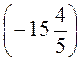 = 0;
= 0;
В) -4х = -8,8; -6y = -36; -6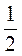 Х = 1;
Х = 1;
Г) -3,7 : (-х) = -1; – х : 4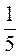 = 0; – х : (-8,7) = 1.
= 0; – х : (-8,7) = 1.
3. Розв’яжіть рівняння: а)  Х = –
Х = –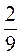 ; б) –
; б) –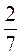 Х = –
Х = – ; в) -2
; в) -2 Х =
Х = 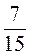 .
.
4. Знайдіть корінь рівняння:
A) 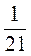 Y –
Y –  Y –
Y – 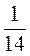 Y =
Y = 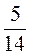 ;
;
Б) 0,4z – 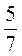 Z = 4,4;
Z = 4,4;
В) 4(0,2х – 7) -5-(0,3х + 6) = 5;
Г) 22,4-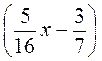 – 35,1
– 35,1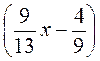 = -45,9.
= -45,9.
Додаткова вправа
Перше число на 2,9 більше за друге. Якщо перше число збільшити у 1,7 раза, а друге – у 1,9 раза, то різниця цих нових значень дорівнює 11,59. Знайдіть дані числа (складіть рівняння за умовою задачі та розв’яжіть його).
IV. Підсумки уроку
Тестові завдання
1. В якому з наведених випадків ділення виконано неправильно?
1) -75 : 5 = 15;
2) -169 : (-13) = -13;
3) 210 : (-10) = -21; 4) 0 : (-47) = 0.
2. Знайдіть суму: (-8 + 24) : (-1 – 3) + 4.
1) 8; 2) 0; 3) -8; 4) -4.
3. Який з поданих виразів дорівнює -4, якщо k = -2?
1) (-k – 15k) : 4;
2) (3k – 9k) : (-3);
3) (10 – k) : (-6);
4) (6k – 12) : 3.
4. Яке з поданих чисел дорівнює частці коренів рівнянь 2х – 5 – 6х = 11 та -5х + 11х + 7 = 13?
1) 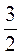 ; 2) -4; 3) –
; 2) -4; 3) –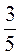 ; 4) 4.
; 4) 4.
5. Обчисліть модуль виразу (-b – 48) : (-16) + b, якщо b = -16.
1) -14; 2) 12; 3) 14; 4) 20.
V. Домашнє завдання
1. До частки чисел – 7,5 і – 3 додайте добуток чисел – 0,3 і 30.
2. До добутку чисел – 1,8 і 2 додайте частку чисел 24 і – 1,2.
3. Розв’яжіть рівняння:
А) х – 2,3 = -4,2;
Б) 2х + 3,6 = 5;
В) 20 – (5 – 4х) = 3;
Г) 14 – (-5 + 2х) = -3.
4. Розв’яжіть рівняння: а) 3х – (х + 17) = 21; б) 10 – 2(7 – х) = 8.
5. Обчисліть: -2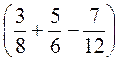 + (9,7 – 1,6) : (-0,9).
+ (9,7 – 1,6) : (-0,9).
6. Спростіть вираз:
А) 2(4a – 5) – (2 – 3а);
Б) -3(5 – 7х) + 4(х – 7);
В) 1,5(2 – 0,2а) + 3(-а + 1);
Г) -2(-1 – 2a + 7b) – (4a – 8b + 1);
Д) –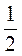 (0,5х – 1,1) –
(0,5х – 1,1) – 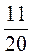 Х;
Х;
Є) (-0,25х + 0,3y) – 3(0,7х – 0,3у).