Дільники і кратні
Математика – Алгебра
Подільність натуральних чисел
Дільники і кратні
Дільником натурального числа а називають натуральне число, на яке а ділиться без остачі.
Кратним натуральному числу а називається натуральне число, яке ділиться на а без остачі.
Приклади
1) Число 12 має 6 дільників: 1, 2, 3, 4, 6, 12. (Зверніть увагу: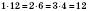 
.)
2) Запишемо п’ять перших чисел, кратних числу 7: 7, 14, 21, 28, 35.
(Зверніть увагу: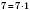 
, 
, 
, 
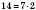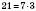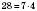
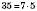.)Число 1 є дільником будь-якого натурального числа. Число 1 має лише один дільник – 1.
Усі інші натуральні числа мають не менше двох дільників: найменший із них – одиниця, найбільший – саме це число.
Кожне натуральне число має безліч кратних, найменшим із яких є саме це число.
Щоб одержати всі числа, кратні числу n, треба множити це число послідовно на всі натуральні числа. Нариклад, запишемо всі числа, кратні 9: 9, 18, 27, 36, … Загальний вигляд числа, кратного 9: 9n, де n – довільне натуральне число.
Загальний вигляд числа b, яке при діленні на число а дає
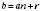, де n – довільне натуральне число, 
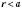.Числа, кратні 2, називаються Парними, а ті, що на 2 не діляться,- Непарними.
Ознака подільності на 2. На 2 діляться ті й тільки ті натуральні числа, запис яких закінчується парною цифрою (тобто 0, 2, 4, 6, 8).
Слова “ті й тільки ті” означають, що у даному випадку є правильними такі два твердження.
1. Якщо запис числа закінчується парною цифрою, то це число ділиться на 2.
2. Якщо число ділиться на 2, то його запис закінчується парною цифрою.
Ознака подільності на 10. На 10 діляться ті й тільки ті натуральні числа, запис яких закінчується цифрою 0. (Аналогічні ознаки можна сформулювати для чисел 100, 1000 і т. д.)
Ознака подільності на 5. На 5 діляться ті й тільки ті натуральні числа, запис яких закінчується цифрами 0 або 5.
Ознака подільності на 3. На 3 діляться ті й тільки ті натуральні числа, сума цифр яких ділиться на 3.
Ознака подільності на 9. На 9 діляться ті й тільки ті натуральні числа, сума цифр яких ділиться на 9.
Ознака подільності на 4(25). На 4 (25) діляться ті й тільки ті натуральні числа, двома останніми цифрами яких записано число, що ділиться на 4 (25).
Запис a b означає, що а кратне b.
Приклади
1)
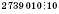, тому що остання цифра числа – 0;3 256 041 не кратне 10 (остання цифра 1).
2)
; 
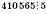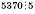;19 372 не кратне 5.
3)
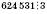, тому що сума цифр 
, 
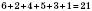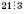;624 532 не кратне 3, тому що сума цифр – число 22 – не кратне 3.
4)
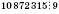, тому що сума цифр 
, 
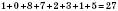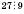;5)
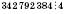, тому що 
;
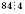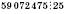, тому що 
.
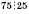(1 votes, average: 5.00 out of 5)
Loading...