Головна ⇒ 📌Математика ⇒ ДОДАВАННЯ НАТУРАЛЬНИХ ЧИСЕЛ

ДОДАВАННЯ НАТУРАЛЬНИХ ЧИСЕЛ

РОЗДІЛ 2 ДІЇ ПЕРШОГО СТУПЕНЯ З НАТУРАЛЬНИМИ ЧИСЛАМИ

§ 7. ДОДАВАННЯ НАТУРАЛЬНИХ ЧИСЕЛ

Ви знаєте, що додавання – це арифметична дія. Числа, які потрібно додати, називаються доданками. Число, яке отримують у результаті додавання, називається сумою.

Складемо рівність на додавання за малюнком 94.

ДОДАВАННЯ НАТУРАЛЬНИХ ЧИСЕЛ

Мал. 94

ДОДАВАННЯ НАТУРАЛЬНИХ ЧИСЕЛ

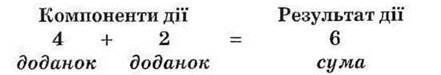
Вираз 4 + 2 також називається сумою.

? Чи зміниться сума, якщо поміняти місцями доданки? Ні. Справді, 4 + 2 = 2 + 4 = 6.

Така властивість додавання справджується для будь-яких

чисел а і b і називається переставним законом додавання.

Переставний закон додавання.

Від перестановки доданків сума не змінюється.

А + b = b + а.

Зрозуміло, що коли один із доданків дорівнює 0, то сума дорівнює іншому доданку:

А + 0 = 0 + а = а.

Ви знаєте, що багатоцифрові числа зручніше додавати у стовпчик. Наприклад, треба знайти суму чисел 4523 і 38245. Для цього розміщують доданки один під одним так, щоб одиниці містилися під одиницями, десятки – під десятками, сотні – під сотнями і т. д. Оскільки а + b = b + а, то для зручності додавання першим, як правило, ставлять більше число. Додавання виконують порозрядно,

починаючи з найменшого розряду – одиниць:

ДОДАВАННЯ НАТУРАЛЬНИХ ЧИСЕЛ

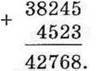
Розглянемо, які задачі можна розв’язувати за допомогою додавання.

Задача 1. Як відомо, Карлсон – дуже великий ласун. На свій день народження він із задоволенням з’їв 6 банок суничного варення до обіду, а після обіду – ще 8 банок. Скільки банок суничного варення з’їв Карлсон?

Розв’язання. Щоб знайти кількість банок суничного варення, які з’їв Карлсон, треба знайти суму двох чисел: 6 і 8. Звідси 6 + 8 = 14 (банок). Отже, Карлсон з’їв 14 банок суничного варення.

Задача 2. Ласун Карлсон дуже скромний. Тому в гостях у Малюка він пригостився лише 2 тістечками. Але цукерок з’їв на 5 штук більше, ніж тістечок. Скільки цукерок з’їв Карлсон?

Розв’язання. Щоб знайти кількість цукерок, які з’їв Карлсон, треба кількість тістечок збільшити на 5. Звідси

2 + 5 = 7 (цукерок). Отже, Карлсон з’їв 7 цукерок.

Зверніть увагу:

За допомогою додавання:

1) знаходять суму двох або більше чисел;

2) збільшують число на вказану кількість одиниць.

Подивіться на малюнок 95. Ви бачите, як на координатному промені число 2 збільшували на 5 одиниць. Для цього від числа 2 у напрямку стрілки (тобто від нього праворуч) відклали 5 одиничних відрізків. Дістали: 2 + 5 = 7.

ДОДАВАННЯ НАТУРАЛЬНИХ ЧИСЕЛ

Мал. 95

Ви вже знаєте, що результат додавання кількох доданків не залежить від порядку їх додавання. Наприклад, щоб знайти суму чисел 36, 11 і 9, можна спочатку додати числа 36 і 11, а потім до їх суми додати число 9. Але зручніше спочатку додати числа 11 і 9 і вже їх суму додати до числа 36. Порядок додавання чисел указують за допомогою дужок. Для розглянутого прикладу дістанемо: (36 + 11) + 9 = 36 + (11 + 9).

Така властивість додавання справджується для будь-яких чисел а, b і с і називається сполучним законом додавання.

Сполучний закон додавання.

Від групування доданків сума не змінюється.

(а + b) + с = а + (b + с).

Зверніть увагу:

Спираючись на сполучний закон додавання, діють за правилом: щоб до суми двох чисел додати третє число, можна до першого числа додати суму другого і третього.

Додавати можна не тільки числа і числові вирази, а й буквені вирази. Наприклад, у сумі а + а + а три рівних

Доданки а, тому а+а+а=а∙3=3∙а=3а. І навпаки, вираз За можна розуміти, як суму трьох рівних доданків, кожен з яких дорівнює а. Тому можемо записати:

3а = а + а + а.

Задача 3. Знайдіть суму 2с + 3d + с + d.

Розв’язання. Застосувавши переставний і сполучний закони додавання, згрупуємо окремо доданки з буквою с і доданки з буквою d:

2с + 3d + с + d – (2с + с) + (3d + d).

Оскільки 2с = с + с, то 2с + с = с + с + с = 3с. Аналогічно, оскільки 3d = d + d + d, тo 3d + d = d + d + d + d = 4d. Тому (2с + с) + (3d + d) = 3c + 4d. Отже, 2с + 3d + с + d = Зс + 4d.

Зверніть увагу:

Додавати можна лише такі буквені вирази, кожен з яких містить ті самі букви.

Дізнайтеся більше

Для обчислення суми чисел в нагоді можуть стати такі властивості додавання.

Якщо один із доданків збільшити (зменшити) на деяке число, то сума збільшиться (зменшиться) на те саме число. Наприклад,

23 + 4 = 27, а (23 + 10) + 4 = 37 і 23 + (4 + 10) = 37.

Якщо один із доданків збільшити на одне число, а другий доданок – на інше число, то сума збільшиться на суму даних чисел. Наприклад,

23 + 4 = 27, а (23 + 10) + (4 + 2) = 39.

Якщо один із доданків збільшити на деяке число, а другий доданок зменшити на те саме число, то сума не зміниться. Наприклад,

23 + 4 = 27, а (23 + 3) + (4 – 3) = 27.

РОЗВ’ЯЖІТЬ ЗАДАЧІ

208. Чи правильно, що в рівності 1084 + 111 = 1195 доданком є число:

1) 1084; 2)111; 3)1195?

209. Чи правильно, що в рівності 54321 = 54300 + 21 сумою є число:

1)54321; 2)21; 3)54300?

210. Обчисліть усно:

1)200 + 250000; 2) 15000000 + 40000.

Яку дію ви виконали? Назвіть компоненти і результат дії.

211. Чи правильно, що 23437 + 78956 = 78956 + 23437? Який закон додавання застосували?

212. Обчисліть:

1)56789 + 0; 2)0 + 3004002009.

213. Число 25 збільшили на: 1) 5; 2) 125; 3) 95; 4) 100000. Яке число отримали?

214. За даними таблиці 6 виконайте дію.

Таблиця 6

Доданок

1 210

462

14117

210

20000560 12300675

Доданок

701587

510123

5 452

65789

345000000176543210

Сума

215. Знайдіть суму чисел:

1) один мільйон триста сорок п’ять тисяч двадцять один і сімсот тисяч двадцять п’ять;

2) сімдесят дев’ять тисяч сто сорок і вісімдесят чотири тисячі;

3) двадцять три мільйони і двадцять три.

216.Порівняйте значення числових виразів:

1) 153000+ 22 і 22+153000;

2) 12056 + 6078 і 6078 + 1256;

3) 300400500 + 23456 і 30040500 + 23456;

4) 2300460 і 333+ 1967.

217. Виконайте додавання:

1) 100 км 17 м + 15 км 23 м; 4) 5 кг 2 г + 115 кг 8 г;

2) 124 км 64 м + 26 км 6 м; 5) 3 год 32 хв + 12 год 24 хв;

3) 16 кг 346 г + 71 кг 4 г; 6)7 год 52 хв + 5 хв.

218. Накресліть координатний промінь. Позначте на ньому число 5. Покажіть на координатному промені, як збільшити дане число на:

1)4; 2)2; 3)10.

Яке число отримали?

219. Накресліть координатний промінь. Позначте на ньому число 3. Покажіть на координатному промені, як збільшити дане число на:

1)8; 2)4; 3)12.

Яке число отримали?

220. Виконайте додавання зручним способом:

1) 12030 + 330 + 670; 4) 1150 + 40010 + 850 + 60090;

2) 175+1619 + 225; 5)20006 + 20012 + 31+6944 + 9 + 888;

3) 1013 + 2000900 + 87; 6)222222 + 33333 + 77777 + 888888.

Яким законом додавання ви скористалися?

221. Спираючись на сполучний закон, виконайте додавання зручним способом:

1) 11001 +197 + 9009;

2)7820 + 105+ 1180;

3) 60005070 + 5002701+ 805030 + 4187199;

4) 16845 + 1234 + 221855 + 66.

222. Порівняйте значення числових виразів:

1) 400094 +20900 + 6 і 401543 + 11267 + 190;

2)30000005 + 2300000 + 5 і 323000005.

223. Знайдіть значення суми а + с, якщо:

1 ) а= 12889, с = 987111;

2) а = 5555555,с = 444445;

3) а = 1234567890,с = 76543210.

Чому дорівнює сума с + а?

224. Швидкість літака дорівнює 720 км/год. Якою стане його швидкість після її збільшення на:

1) 5 м/год; 2) 5 м/хв; 3) 5 м/с?

225. У 2010 році в математичному конкурсі “Кенгуру” брало участь 469554 учні України, а в 2011 році – на 143113 учнів більше. Скільки учнів брало участь у конкурсі за ці два роки?

226. У математичному турнірі з міста А брало участь d учнів, а з міста В – нa c учнів більше. Скільки всього учнів із цих міст брало участь у турнірі?

227. Стадіон “Донбас Арена” в Донецьку може прийняти 51504 вболівальники, стадіон “Олімпійський” у Києві – 70050 вболівальників, а стадіон “Арена Львів” у Львові – 34915 вболівальників. Скільки всього вболівальників можуть прийняти ці три стадіони?

228. Стадіон А може прийняти n вболівальників, стадіон В – m вболівальників, стадіон С – k вболівальників. Скільки всього вболівальників можуть прийняти три стадіони?

229. Складіть задачу за виразом:

1 )m+n4 2 )m+(m+n); 3 )р+m + n.

230. Знайдіть суму;

1)348 + 493; 4) 15923 + 89989;

2)2868 + 642 + 100; 5) 424592 + 3575408;

3)30925 + 84553; 6)999999+ 111111.

231. Як зміниться сума, якщо один доданок збільшити на 80008, а другий на 765?

232. Розставте суми чисел 1020304 + 102030, 652356 + 376583, 111111 + 100015 + 336 і 34067 + 0 у порядку спадання.

233. Розставте суми чисел 9544 + 102320, 52356 + 60583 і 1001 + 9000 + 540 + 460 у порядку зростання.

234. Виконайте додавання:

1) 1234 км 17 м + 167 км 87 м;

2) 62 кг 346 г + 79 кг 786 г;

3) 15 год 48 хв 58 с + 6 год 24 хв 15 с;

4) 4 год 32 хв 34 с + 27 хв 26 с.

235. Знайдіть суму найбільших п’ятицифрового, чотирицифрового і двоцифрового чисел.

236. Знайдіть суму найменших п’ятицифрового, чотирицифрового і двоцифрового чисел.

237. Накресліть координатний промінь. Позначте на ньому точки А(2) і В(6). Покажіть, як побудувати точку С, координата якої є сумою координат даних точок.

238. Накресліть координатний промінь. Позначте на ньому точки А(7) і B(3). Покажіть, як побудувати точку С, координата якої є сумою координат даних точок.

239. Обчисліть зручним способом:

1) 1 + 12 + 23 + 34 + 45 + 56 + 67 + 78 + 89 + 90;

2)145+146 + 147+148+149+150+151 + 152+153+154+155.

240. Знайдіть значення виразу:

1)2а + 2b, якщо а + b = 1843;

2)х ∙ 3 + у ∙ 3, якщо х + у = 507.

241. Знайдіть суму:

1) 6а + 5n + 5 + 4а + 14m + 9m + 28;

2) c + 5d + 2c + d ∙ 5.

242. Чому дорівнює значення суми а + с + p, якщо:

1) а = 56, с = 567 + 87, р = 112 + 76;

2) а = 93 + 39, с = 38, р = 105 + 45 + 23?

243. Довжина відрізка АВ дорівнює 248 м 65 см. Відрізок CD довший за відрізок АВ на 52 м 35 см і коротший від відрізка MN на 67 м. Знайдіть суму довжин відрізків АВ, CD і MN.

244 Довжина відрізка AS дорівнює 43 м 24 см. Відрізок CD довший за відрізок АВ на 56 м 76 см і коротший від відрізка MN на 5 м 23 см. Знайдіть суму довжин відрізків АВ, CD і MN.

245. У школі № 1 навчається р учнів, у школі № 2 – на n учнів більше, а в школі № 3 – на m учнів більше, ніж у школі № 2. Скільки учнів навчається в кожній школі? Скільки учнів навчається в трьох школах?

Розв’яжіть задачу, якщо:

1)р = 673, n = 453, m = 232; 2)р = 942, n = 361, m= 1004.

246. Запишіть число 5678 у вигляді суми трьох чисел, перше з яких є найменшим чотирицифровим числом, а друге – найбільшим трицифровим.

247. Поставте знаки “+” між числами так, щоб рівність була правильною:

1)5555 555 = 665; 2)5555555 = 125.

248. Знайдіть суму чисел 1 +2 +….+ 99 + 100.

249. Замість * вставте пропущені цифри:

ДОДАВАННЯ НАТУРАЛЬНИХ ЧИСЕЛ

ЗАСТОСУЙТЕ НА ПРАКТИЦІ

250. Відстань від Харкова до Києва дорівнює 483 км. Вона на 294 км більша, ніж відстань від Києва до Черкас, і на 142 км

Більша за відстань від Черкас до Вінниці. Яку відстань подолав турист маршрутом Харків – Київ – Черкаси – Вінниця?

251. Дерево гінко з’явилося на Землі дуже давно. В Японії та Китаї його вважають священним і вирощують біля храмів. Висота цих дерев досягає 30 м. Щоб дізнатися, скільки років тому з’явилося це дерево, обчисліть суму 99999 + 45627 + + 19287345+15567029.

252. Швидкість звуку дорівнює 344 м/с, що на 299 792 115 м/с менше, ніж швидкість світла. Знайдіть швидкість світла.

ЗАДАНІ НА ПОВТОРЕННЯ

253. Обчисліть:

1) 12 + 50+15+16 + 30 + 45; 2)27 + 70 + 48 + 52 + 30+13.

254. У 5-Б класі навчається 28 учнів, у 5-В – на 6 учнів більше, а в 5-А – на 4 учні менше, ніжу 5-В. Скільки учнів у кожному класі?

255. Василько має в понеділок п’ять уроків по 45 хв. Перший урок розпочинається о 8 год. О котрій годині закінчується останній урок, якщо перерви тривають по 10 хв?


1 Звезда2 Звезды3 Звезды4 Звезды5 Звезд (1 votes, average: 5.00 out of 5)
Loading...


Related posts:

  1. Властивості додавання натуральних чисел УРОК 19 Тема. Властивості додавання натуральних чисел Мета: повторити і систематизувати знання учнів про переставну і сполучну властивості додавання; сформувати навички застосування властивостей додавання під час розв’язання вправ на додавання. Тип уроку: комбінований. Обладнання: схема “Властивості додавання”. Хід уроку I. Перевірка домашнього завдання № 197 1) II. Актуалізація опорних знань Усні вправи 1. Знайдіть суму […]...

  2. Додавання натуральних чисел. Властивості додавання Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 3. Додавання натуральних чисел. Властивості додавання З початкових класів відомо, як додавати невеликі натуральні числа. Розглянемо задачу. Задача. У 5-А класі 27 учнів, а в 5-Б – 29 учнів. Скільки учнів у двох класах? Розв’язання. 27 + 29 = 56. Ця задача […]...

  3. Strong>Додавання натуральних чисел. Властивості дії додавання 4. Додавання і віднімання багатоцифрових чисел Додавання натуральних чисел. Властивості дії додавання Будь-які два натуральні числа можна додати. Додавання – це арифметична дія, за допомогою якої знаходять число, що складається зі стількох одиниць, скільки їх є в усіх доданках разом. Сума натуральних чисел завжди більша від кожного з доданків. Для швидкого і раціонального обчислення треба […]...

  4. Додавання натуральних чисел. Властивості додавання УРОК 20 Тема. Додавання натуральних чисел. Властивості додавання Мета: закріпити знання учнів про властивості додавання натуральних чисел; відпрацювати навички додавання багатоцифрових натуральних чисел; додавання величин і застосування переставної та сполучної властивостей додавання для раціоналізації обчислень. Тип уроку: застосування знань, навичок та вмінь. Обладнання: таблиця-схема “Властивості додавання”. Хід уроку І. Перевірка домашнього завдання На дошці скорочено […]...

  5. Додавання і віднімання натуральних чисел. Вирази УРОК 27 Тема. Додавання і віднімання натуральних чисел. Вирази Мета: перевірити засвоєння учнями теми “Додавання і віднімання натуральних чисел. Вирази”. Тип уроку: перевірка та корекція знань, навичок та вмінь. Хід уроку Тематична контрольна робота № 2 Варіант 1 1. Обчисліть: 1) 5 693 + 29 758; 2) 42 735 – 4 028. 2. На одній […]...

  6. Додавання натуральних чисел. Переставна і сполучна властивість додавання Урок № 8 Тема. Додавання натуральних чисел. Переставна і сполучна властивість додавання Мета. Узагальнити знання учнів про додавання натуральних чисел з початкових класів, ввести правило додавання натуральних чисел, переставний і сполучний закони додавання, формувати навички додавання багатоцифрових натуральних чисел та розв’язування задач більш складного характеру; розвивати пізнавальну самостійність, увагу, пам’ять; виховувати культуру математичної мови, записів […]...

  7. Аналіз контрольної роботи. Додавання натуральних чисел. Закони додавання. Задачі, які розв’язуються додаванням (№№ 374-381) Тема. Аналіз контрольної роботи. Додавання натуральних чисел. Закони додавання. Задачі, які розв’язуються додаванням (№№ 374-381). Мета. Проаналізувати допущені під час контролю знань помилки та організувати роботу над ними; узагальнити уявлення учнів про дію додавання та її закони, а також задачі на додавання та способи їх розв’язування. Обладнання. Схеми задач; демонстраційний матеріал. Зміст уроку І. Аналіз […]...

  8. ДІЯ ДОДАВАННЯ. НАЗВИ КОМПОНЕНТІВ І РЕЗУЛЬТАТУ ДІЇ ДОДАВАННЯ. ЗНАХОДЖЕННЯ СУМИ ЧИСЕЛ. ДОПОВНЕННЯ РІВНОСТЕЙ ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 40. ДІЯ ДОДАВАННЯ. НАЗВИ КОМПОНЕНТІВ І РЕЗУЛЬТАТУ ДІЇ ДОДАВАННЯ. ЗНАХОДЖЕННЯ СУМИ ЧИСЕЛ. ДОПОВНЕННЯ РІВНОСТЕЙ Мета: ознайомити учнів з термінами “доданок” і “сума”; вчити користуватися числовим відрізком під час розв’язування прикладів на додавання; розвивати мислення; виховувати інтерес до предмета. Хід уроку I. […]...

  9. Ознаки подільності натуральних чисел на 2, 5, 10, 3 і 9 Урок № 3 Тема. Ознаки подільності натуральних чисел на 2, 5, 10, 3 і 9 Мета: відпрацювати навички використання ознак подільності і понять уроку №1 для виконання завдань, що передбачають означення подільності чисел. Тип уроку: засвоєння вмінь і навичок. Хід уроку І. Перевірка домашнього завдання 1. Ігровий момент @Учитель заздалегідь виготовляє картки з правильними і […]...

  10. АЛГОРИТМ ПИСЬМОВОГО ДОДАВАННЯ ЧИСЕЛ. КУБ ДІЇ З БАГАТОЦИФРОВИМИ ЧИСЛАМИ. ПИСЬМОВЕ ДОДАВАННЯ І ВІДНІМАННЯ АЛГОРИТМ ПИСЬМОВОГО ДОДАВАННЯ ЧИСЕЛ. КУБ 544. Прочитай коротке пояснення письмового додавання. 1. Записую розряди під однойменними розрядами. 2. Починаю додавання з одиниць: 4 + 8 = 12, 2 пишу під одиницями, 1 десяток надписую над десятками. 1 + 9 = 10 та ще 1 буде 11, 1 […]...

  11. ПИСЬМОВЕ ДОДАВАННЯ Й ВІДНІМАННЯ ЧИСЕЛ ПОВТОРЕННЯ МАТЕРІАЛУ ЗА 3 КЛАС ПИСЬМОВЕ ДОДАВАННЯ Й ВІДНІМАННЯ ЧИСЕЛ 39. Розв’яжи задачу складанням виразу. У хорі Будинку творчості 85 дітей, у гуртку з моделювання на 39 дітей менше, ніж у хорі, а в танцювальних колективах на 19 дітей більше, ніж у хорі й гуртку з моделювання разом. Скільки дітей займаються в танцювальних колективах? 40. […]...

  12. Додавання натуральних чисел Урок № 9 Тема. Додавання натуральних чисел Мета: удосконалювати вміння і навички учнів розв’язувати приклади і задачі на додавання натуральних чисел; розвивати увагу, аналітичне, логічне, творче мислення; виховувати працелюбність, реалізуючи принципи виховання в колективі і через колектив, культуру математичної мови. Обладнання: графо-проектор, дидактичний матеріал, кодопозитиви, мікрокалькулятори. Хід уроку І. Контроль, корекція і закріплення знань. 1. […]...

  13. ДОДАВАННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ Розділ 4 РАЦІОНАЛЬНІ ЧИСЛА ТА ДІЇ З НИМИ § 26. ДОДАВАННЯ РАЦІОНАЛЬНИХ ЧИСЕЛ Кожне раціональне число характеризують його модуль і знак. Тому для додавання двох раціональних чисел важливо з’ясувати, яким буде модуль і знак суми залежно від модулів і знаків доданків. Для додатних чисел цей зв’язок очевидний, оскільки сума двох додатних чисел є числом додатним. […]...

  14. ЗАКРІПЛЕННЯ ДОДАВАННЯ І ВІДНІМАННЯ ДВОЦИФРОВИХ ЧИСЕЛ. САМОСТІЙНА РОБОТА УСНЕ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ У МЕЖАХ 100 З ПЕРЕХОДОМ ЧЕРЕЗ РОЗРЯД Урок 48. ЗАКРІПЛЕННЯ ДОДАВАННЯ І ВІДНІМАННЯ ДВОЦИФРОВИХ ЧИСЕЛ. САМОСТІЙНА РОБОТА Мета: удосконалити навички додавання і віднімання двоцифрових чисел; закріпити вміння розв’язувати задачі на дві дії; розвивати математичне мовлення; виховувати інтерес до математики, самостійність. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. […]...

  15. ДІЯ ДОДАВАННЯ. ЗАКОНИ ДОДАВАННЯ. ТАБЛИЧНЕ Й ПОЗАТАБЛИЧНЕ, УСНЕ І ПИСЬМОВЕ ДОДАВАННЯ. ЗАДАЧІ, ЯКІ РОЗВ’ЯЗУЮТЬСЯ ДОДАВАННЯМ Мета: узагальнити уявлення учнів про дію додавання та її закони; закріпити вміння розв’язувати задачі на додавання; повторити прийоми письмового додавання трицифрових чисел; розвивати уважність; виховувати інтерес до предмета. ХІД УРОКУ I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. КОНТРОЛЬ, КОРЕКЦІЯ І ЗАКРІПЛЕННЯ ЗНАНЬ 1. Перевірка домашнього завдання 2. Усні обчислення Гра “Ланцюжок” Зменшуване 400, від’ємник 120, знайди різницю; до […]...

  16. Додавання двох чисел з різними знаками Розділ 4 Раціональні числа і дії мідними §39. Додавання двох чисел з різними знаками Припустимо, що в понеділок Іван заборгував Сергію 3 грн, а у вівторок повернув борг, тобто віддав Сергію 3 грн. Оскільки борг можна тлумачити як від’ємні числа, а майно – як додатні, то розрахунок між хлопцями можна подати так: -3 + 3 […]...

  17. ТАБЛИЦЯ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ. РОЗВ’ЯЗУВАННЯ ЗАДАЧ ЗА ПЛАНОМ ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ. ЗАДАЧІ НА ДВІ ДІЇ. ВИРАЗИ З ДУЖКАМИ ЗАДАЧІ НА ДВІ ДІЇ Урок 25. ТАБЛИЦЯ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ. РОЗВ’ЯЗУВАННЯ ЗАДАЧ ЗА ПЛАНОМ Мета: узагальнити знання таблиць додавання і віднімання чисел; формувати вміння розв’язувати задачі за планом; виховувати пізнавальний інтерес до вивчення математики. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ […]...

  18. Додавання раціональних чисел з різними знаками Урок № 7 1 Тема. Додавання раціональних чисел З різними знаками Мета: сформувати уявлення учнів про зміст дії додавання раціональних чисел з різними знаками (в тому числі й протилежних чисел), а також виробити вміння використовувати це правило під час додавання двох раціональних чисел з різними знаками. Обладнання: демонстраційний термометр. Тип уроку: засвоєння навичок та вмінь. […]...

  19. Додавання від’ємних чисел Розділ 4 Раціональні числа і дії мідними §38. Додавання від’ємних чисел Нехай у понеділок Іван узяв у Сергія в борг 2 грн, а у вівторок – ще 3 грн. Тоді за два дні разом борг складає 2 + 3 = 5 (грн). Борг можна тлумачити як від’ємні числа. Тому суму боргу за два дні можна […]...

  20. Ряд натуральних чисел Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 1. НАТУРАЛЬНІ ЧИСЛА Вивчивши матеріал цього параграфа, ви розширите свої знання про натуральні числа та форму їх запису, навчитеся зручного способу порівняння натуральних чисел, дізнаєтеся, що таке координатний промінь і як можна позначати на ньому точками натуральні числа. Ознайомитеся з властивостями прямої, променя і відрізка. 1. […]...

  21. Величини. Метрична система мір. Додавання й віднімання багатоцифрових чисел УРОК 130 Тема. Величини. Метрична система мір. Додавання й віднімання багатоцифрових чисел Мета: узагальнити й систематизувати знання учнів про дії додавання й віднімання багатоцифрових чисел, їх закони; вдосконалювати навички усної лічби. ХІД УРОКУ I. Контроль і закріплення знань учнів Усні обчислення – Обчислити зручним способом. 130 + 250 + 170 + 250 147 – (47 […]...

  22. Розв’язування задач на додавання і віднімання натуральних чисел Урок № 12 Тема. Розв’язування задач на додавання і віднімання натуральних чисел Мета. Удосконалювати вміння і навички розв’язування різних типів задач на додавання і віднімання натуральних чисел; систематизувати відомі прийоми розв’язування задач; формувати вміння виявляти закономірності, узагальнювати, проводити міркування за аналогією; розвивати творче мислення, активність, пізнавальну самостійність; виховувати інтерес і любов до предмета математики. Обладнання: […]...

  23. Множення натуральних чисел Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 5. Множення натуральних чисел Як відомо з молодших класів, суму однакових доданків можна записати коротше за допомогою множення. Наприклад: 45 + 45 + 45 + 45 = 45 ∙ 4 = 180. Читають так: “по 45 взяти 4 рази” або “45 помножити […]...

  24. Властивості додавання раціональних чисел Урок № 7 2 Тема. Властивості додавання раціональних чисел Мета: повторити зміст переставної та сполучної властивостей додавання та відпрацювати застосування цих законів додавання в комплексі із вивченими правилами додавання раціональних чисел. Тип уроку: застосування знань, умінь, навичок. Хід уроку І. Перевірка домашнього завдання 1. Фронтальна робота із сигнальними картками 1) Заповніть пропуски в реченнях: А) […]...

  25. НУМЕРАЦІЯ ЧИСЕЛ 1-100. ВИПАДКИ ДОДАВАННЯ І ВІДНІМАННЯ В МЕЖАХ 100, ПОВ’ЯЗАНІ З НУМЕРАЦІЄЮ ЧИСЕЛ. РОЗВ’ЯЗУВАННЯ ПРОСТИХ ЗАДАЧ ПОВТОРЕННЯ МАТЕРІАЛУ ЗА 1-Й КЛАС Урок 1. НУМЕРАЦІЯ ЧИСЕЛ 1-100. ВИПАДКИ ДОДАВАННЯ І ВІДНІМАННЯ В МЕЖАХ 100, ПОВ’ЯЗАНІ З НУМЕРАЦІЄЮ ЧИСЕЛ. РОЗВ’ЯЗУВАННЯ ПРОСТИХ ЗАДАЧ Мета: повторити нумерацію чисел 1-100; вдосконалити обчислювальні навички, вміння розв’язувати прості задачі; розвивати кмітливість, мислення учнів; виховувати інтерес до математики. Хід уроку I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ 1. Ознайомлення […]...

  26. Читання і записування п’ятицифрових чисел у межах 20 тисяч. Письмове додавання трицифрових чисел. Задачі на знаходження третього доданка (№№ 206-216) Тема. Читання і записування п’ятицифрових чисел у межах 20 тисяч. Письмове додавання трицифрових чисел. Задачі на знаходження третього доданка (№№ 206-216). Мета. Ознайомити учнів з утворенням, називанням, читанням і записуванням п’ятицифрових чисел у межах 20 тисяч; повторити правило письмового додавання трицифрових чисел; виправляти учнів у розв’язанні задач на знаходження третього доданка. Обладнання. Нумераційна таблиця; картки […]...

  27. Віднімання натуральних чисел Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 4. Віднімання натуральних чисел Розглянемо задачу. Задача 1. Пішохід за дві години пройшов 7 км. Скільки кілометрів він пройшов за другу годину, якщо за першу подолав 4 км? У цій задачі число 7 є сумою числа 4 і невідомого числа: 4 + […]...

  28. Властивості додавання Розділ 4 Раціональні числа і дії мідними §40. Властивості додавання Для додавання раціональних чисел, як і для додавання додатних чисел, справджуються переставна і сполучна властивості. Переставна властивість додавання. Для будь-яких раціональних чисел а і b виконується рівність а + b = b + а. Перевіримо цю властивість на прикладах. Приклад 1. -8 + (-3) = […]...

  29. Додавання і віднімання багатоцифрових чисел Мета: формувати обчислювальні навички Дидактичні задачі. Вдосконалювати навички усних обчислень. Актуалізувати розуміння залежності значення суми від зміни одного з доданків, залежності значення різниці від зміни від’ємника. Актуалізувати прийом округлення при додаванні і відніманні; застосування прийому округлення до випадків додавання і віднімання, чисел, близькі до розрядних одиниць: 99,999,9999… . Формувати навички додавання та віднімання багатоцифрових чисел […]...

  30. АНАЛІЗ КОНТРОЛЬНОЇ РОБОТИ. УСНЕ ДОДАВАННЯ ДВОЦИФРОВИХ ЧИСЕЛ З ПЕРЕХОДОМ ЧЕРЕЗ ДЕСЯТОК УСНЕ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ У МЕЖАХ 100 З ПЕРЕХОДОМ ЧЕРЕЗ РОЗРЯД Урок 34. АНАЛІЗ КОНТРОЛЬНОЇ РОБОТИ. УСНЕ ДОДАВАННЯ ДВОЦИФРОВИХ ЧИСЕЛ З ПЕРЕХОДОМ ЧЕРЕЗ ДЕСЯТОК Мета: ознайомити учнів із загальним випадком усного додавання двоцифрових чисел з переходом через десяток; формувати вміння розв’язувати задачі; розвивати математичну грамотну мову; виховувати інтерес до математики. Хід уроку I. ОРГАНІЗАЦІЙНИЙ […]...

  31. Письмове додавання і віднімання багатоцифрових чисел (№№ 390-396) Тема. Письмове додавання і віднімання багатоцифрових чисел (№№ 390 – 396). Мета. Ознайомити учнів з прийомами письмового додавання і віднімання багатоцифрових чисел у межах мільйона; закріплювати вміння учнів розв’язувати задачі та рівняння. Обладнання. Таблиця усних обчислень; “Картки для поточного контролю знань”; схеми задач. Зміст уроку І. Контроль, корекція і закріплення знань. 1. Перевірка домашньою завдання. […]...

  32. Порівняння натуральних чисел Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 2. Порівняння натуральних чисел Одне з двох різних натуральних чисел завжди більше або менше від іншого. Це означає, що натуральні числа можна порівнювати. Число 5392 більше за число 837 тому, що 5392 – чотирицифрове число, а 837 – трицифрове. Числа 5392 і […]...

  33. ПИСЬМОВЕ ДОДАВАННЯ БАГАТОЦИФРОВИХ ЧИСЕЛ ДІЇ З БАГАТОЦИФРОВИМИ ЧИСЛАМИ. ПИСЬМОВЕ ДОДАВАННЯ І ВІДНІМАННЯ ПИСЬМОВЕ ДОДАВАННЯ БАГАТОЦИФРОВИХ ЧИСЕЛ 533. Прочитай числа в таблиці. Поясни, як знайдено їх суму. Дія Сотні тисяч Десятки тисяч Одиниці тисяч Сотні Десятки Одиниці + 4 2 3 4 2 3 3 6 4 3 6 4 7 8 7 7 8 7 Дія Сотні тисяч Десятки […]...

  34. Письмове додавання й віднімання трицифрових чисел. Знаходження значень буквених виразів. Задачі на 3 дії УРОК 3 Тема. Письмове додавання й віднімання трицифрових чисел. Знаходження значень буквених виразів. Задачі на 3 дії Мета: повторити алгоритм письмового додавання й віднімання чисел; опрацювати розширену задачу на знаходження третього доданка; ознайомити учнів з розміщенням відрізків на площині і в просторі. Обладнання: предметні малюнки, таблиця “Додавання й віднімання трицифрових чисел”. ХІД УРОКУ I. Контроль […]...

  35. ДОДАВАННЯ І ВІДНІМАННЯ КРУГЛИХ БАГАТОЦИФРОВИХ ЧИСЕЛ ЗАСТОСУВАННЯ НУМЕРАЦІЇ ДО ВИКОНАННЯ ДІЙ ДОДАВАННЯ І ВІДНІМАННЯ КРУГЛИХ БАГАТОЦИФРОВИХ ЧИСЕЛ 496. 5 тис. + 4 тис. 2 сот. + 9 сот. 30 дес. + 20 дес. 5 000 + 4 000 8 сот. – 3 сот. 12 сот. – 3 сот. 3 800 + 1 000 3 800 + 100 3 800 + 20 […]...

  36. ЧИСЛОВІ ВИРАЗИ, РІВНОСТІ, НЕРІВНОСТІ. ПОРІВНЯННЯ НАТУРАЛЬНИХ ЧИСЕЛ РОЗДІЛ 1 ЛІЧБА, ВИМІРЮВАННЯ І ЧИСЛА § 4. ЧИСЛОВІ ВИРАЗИ, РІВНОСТІ, НЕРІВНОСТІ. ПОРІВНЯННЯ НАТУРАЛЬНИХ ЧИСЕЛ Ви вже знаєте чотири арифметичні дії над числа­ми – додавання, віднімання, множення і ділення. Щоб записати, яку саме дію над числами треба виконати, використовують числові вирази. Наприклад, записи 24 + 2, 24 – 2, 24 ∙ 2, 24 : 2 […]...

  37. Дроби і ділення натуральних чисел Розділ II ДРОБОВІ ЧИСЛА І ДІЇ З НИМИ § 4. ЗВИЧАЙНІ ДРОБИ 28. Дроби і ділення натуральних чисел Чи можна число 3 поділити на 4? Нібито не можна. Але тоді виходить, що четверо шукачів скарбів, коли знайдуть 3 мішки із золотом, не зможуть розділити здобич? Звісно, зможуть. Наприклад, можна зробити так: поділити кожний великий мішок […]...

  38. НУМЕРАЦІЯ ТРИЦИФРОВИХ ЧИСЕЛ. ЗАПИС ЧИСЕЛ СУМОЮ РОЗРЯДНИХ ДОДАНКІВ. ПИСЬМОВЕ ДОДАВАННЯ І ВІДНІМАННЯ ТРИЦИФРОВИХ ЧИСЕЛ. РОЗМІЩЕННЯ ВІДРІЗКІВ НА ПЛОЩИНІ ОРІЄНТОВНА НАВЧАЛЬНА МЕТА: ЗАКРІПЛЮВАТИ ВМІННЯ ЗАМІНЮВАТИ ТРИЦИФРОВІ ЧИСЛА СУМОЮ ВІДПОВІДНИХ РОЗРЯДНИХ ДОДАНКІВ, ПРИЙОМИ ПИСЬМОВОГО ДОДАВАННЯ І ВІДНІМАННЯ ТРИЦИФРОВИХ ЧИСЕЛ, УМІННЯ ВИРАЗНОГО І ЧІТКОГО ЧИТАННЯ ЗАДАЧ; УДОСКОНАЛЮВАТИ НАВИЧКИ ЗНАХОДЖЕННЯ ЗНАЧЕНЬ БУКВЕНИХ ВИРАЗІВ, УМІННЯ ОПИСУВАТИ ПОЛОЖЕННЯ ВІДРІЗКІВ НА ПЛОЩИНІ I. Перевірка домашнього завдання Запис розв’язання задачі 10 на дошці. Фронтально повідомити значення виразів із вправи 9. На […]...

  39. Ряд натуральних чисел УРОК 3 Тема. Ряд натуральних чисел Мета: узагальнити і поглибити знання учнів про натуральні числа; формувати вміння розпізнавати натуральні числа, наводити їх приклади. Тип уроку: засвоєння нових знань. Хід уроку I. Актуалізація опорних знань @ Оскільки тема не є новою для п’ятикласників, доцільно провести з учнями бесіду: – Скільки тобі років? – Скільки кольорів у […]...

  40. Порівняння, додавання та віднімання раціональних чисел Урок № 8 0 Тема. Порівняння, додавання та віднімання Раціональних чисел Мета: перевірити якість та рівень знань і вмінь учнів, здобутих у ході вивчення теми. Тип уроку: перевірка і корекція знань, умінь і навичок. Хід уроку I. Організаційний момент II. Умови тематичної контрольної роботи Варіант 1 1. Позначте на координатній прямій точки: A(3); B(-4); C(1,5); […]...

Ви зараз читаєте: ДОДАВАННЯ НАТУРАЛЬНИХ ЧИСЕЛ
«
»