Додавання раціональних чисел (з однаковими знаками)
Урок № 7 0
Тема. Додавання раціональних чисел (з однаковими знаками)
Мета: сформувати уявлення про зміст дії додавання раціональних чисел; вивести правила додавання від’ємних чисел і виробити вміння застосовувати це правило для розв’язування задач, що передбачають додавання від’ємних чисел.
Обладнання: демонстраційний термометр.
Тип уроку: засвоєння нових знань.
Хід уроку
I. Актуалізація опорних знань
Усні вправи
1. Обчисліть:
А) 5 + 0,8; 0,23 + 7; 0,48 + 0,2; 0,6 + 0,34; 2,7 + 1,12;
Б) 3,4 + 2,5; 17,2 + 2,8; 5,9 + 3,7; 4,857 + 7,64;
В) 6 +
2. Знайдіть серед чисел від’ємні: -(-4);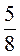 
; -2,3; 
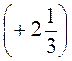; -(-(-3,8)).
3. Чому дорівнюють модулі чисел: 2,7; -3; -2,7; 3; 5,03; а, якщо а > 0; – b, якщо b > 0?
4. Чому дорівнюють значення пропущених цифр (нерівності є правильними):
А) 2,7… > 2,73; б) -2,7… > -2,73; в) 2,7… > -2,73; г) -2,7… > 2,73?
II. Формування знань
@ 1. Традиційно в радянській школі цій темі передувала тема “Зміни величин”, у ході вивчення якої діти усвідомлювали, що зміни величин бувають двох видів: збільшення (зміна вважається додатною) та зменшення (зміна вважається
2. Автор наполягає на тому, що краще не давати правило додавання від’ємних чисел, а провести аналогію з додаванням двох додатних чисел і сформулювати загальне правило додавання двох чисел з однаковими знаками.
Зміст навчального матеріалу може бути таким (працюємо з моделлю термометра):
Задача 1. Термометр показує +3 °С. Потім температура підвищилась на 2 °С. Яку температуру показує термометр зараз?
Розв’язання. Зрозуміло, що +3 + (+2) = 5 або +3 + (+2) + = (|+3| + |+2|) = + (3 + 2)+ = 5.
Задача 2. Термометр показував -4 °С. Потім температура знизилась на 2 °С. Яку температуру показує термометр зараз?
Розв’язання. Зрозуміло, що, як і в попередній задачі, -4 + (-2) = -6.
Звернемо увагу, що -4 + (-2) = (|-4| +|-2|) = -(4 + 2) = -6.
Отже, щоб додати 2 числа з однаковими знаками, достатньо додати їх модулі і перед результатом поставити їх спільний знак.
III. Закріплення знань. Вироблення вмінь
Усні вправи
Виконайте додавання: а) 40 + 60; -40 + (-60); 20 + (+15); -20 + (-15);
Б) 0,3 + 0,7; -0,3 + (-0,7); +1,2 + (0,6); -1,2 + (-0,6);
В)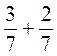 
; 
; 
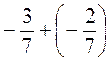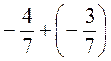; г) 
; 
; 
.
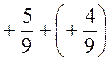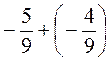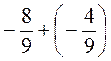Письмові вправи
1. Знайдіть суму чисел:
А) 110 + 120; б) -110 + (-120); в) -107 + (-18); г) -25 + (-50); д) (-0,5) + (-2,5); є) +4,2 + (+5,8); ж) -6,3 + (-4,7); з) -8,5 + (-1,75); к) -1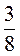
+ 
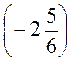; л) -5
+ 
.
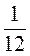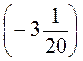2. Увечері температура повітря була-10,5 °С, а за ніч знизилась на 7,9 °С. Яка температура повітря була вранці?
3. Поставте замість * знак “>” або “<“, щоб утворилась правильна нерівність: а) -17 + (-31) * -17; б) -22 + (-35) * -35.
4. Знайдіть значення виразу х + у + (-16), якщо
А) х = -17; у = -19; б) х = -9,1; у = -7,4; в) х = –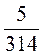
; у = -2
.
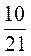Додатково. Вправи на повторення
5. Відомо, що х і у додатні числа. Порівняйте: а) 0 та х; б) – у та 0; в) – х та у; г) у та – х, д) |х| та – х; е) |у| та у; ж) – х та |у|; з) |-х| та – у.
6. На координатній прямій позначено точки A(х) та B(у). Знайдіть координату С середини відрізка АВ, якщо: а) х = 4; у = 8; б) х =-2; у = -4; в) х = -3; у = 5.
IV. Підсумки уроку
Історична довідка. Відомо, що додатні і від’ємні числа були відомі ще давнім індусам. Але, на відміну від нас, вони вважали додатні числа “майном”, а від’ємні числа “боргом”. Спробуйте перекласти вивчене правило додавання чисел з однаковими знаками на мову давніх індусів.
(Правильна відповідь. Борг + борг є борг; майно + майно є майно.)
V. Домашнє завдання
1. Виконайте додавання:
А) -46 + (-18); б) -8 + (-12); в) -144 + (-56); г) -6,4 + (-3,6); д) -5,8 + (-1,8); є) -3,74 + (-1,74);
Ж) –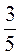
+ 
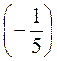; з) –
+ 
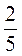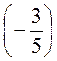; к) –
+ 
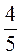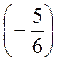; л) -3
+
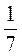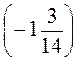; м) -1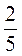+ (-2,8); н) -1
+ (-2,25).
2. Задача. Відстань від Києва до Харкова 500 км; 15 % цієї відстані становить 60 % довжини каналу Сіверський Донець – Донбас. Визначте довжину каналу.
3. Розв’яжіть рівняння: а)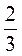 
Х +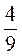 
Х = 3,2; б) х – 0,2х = 
.
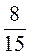(1 votes, average: 5.00 out of 5)
Loading...