Головна ⇒ 📌Плани-конспекти уроків по математиці ⇒ Друга ознака рівності трикутника

Друга ознака рівності трикутника

Урок № 20

Тема. Друга ознака рівності трикутника

Мета: домогтися розуміння учнями другої ознаки рівності трикутників та поняття “сторона і прилеглі до неї кути трикутника”.

Сформувати в учнів первинні уміння:

– знаходити на готових рисунках та в трикутниках, заданих назвою своїх вершин, відповідні сторони і прилеглі до неї кути;

– робити висновки щодо рівності трикутників за знайденими рівними стороною і прилеглими кутами;

– відтворювати зміст теореми, що виражає другу ознаку рівності трикутників та застосовувати

цей зміст до розв’язування задач на доведення рівності трикутників.

Тип уроку: засвоєння знань, умінь та навичок.

Наочність і обладнання: набір демонстраційного креслярського приладдя; таблиця “Ознаки рівності трикутників”.

ХІД УРОКУ

I. Організаційний момент

II. Перевірка домашнього завдання

Запитання до класу

1. Чи можуть три кути трикутника бути прямими? Чому?

2. Поза прямою a дано точку. Скільки через неї можна провести:

А) прямих;

Б) прямих, паралельних до a;

В) прямих, перпендикулярних до a;

Г) перпендикулярів до прямої a.

Як зміняться відповіді на запитання,

якщо точка лежатиме на прямій?

Домашні вправи перевіряємо вибірково, зупинившись на важливих та найскладніших моментах.

III. Мотивація навчальної діяльності. Формулювання мети й завдань уроку

Задача. У трикутнику 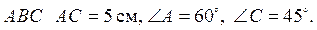Побудуйте трикутник A1B1C1 , в якому 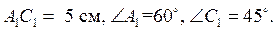Що можна сказати про трикутники ABC і A1B1C1. Чому?

Методичний коментар

Насправді ознаки рівності трикутників у певному вигляді застосовувались учнями ще у 5 класі під час вивчення теми “Трикутник” (у розв’язуванні задач на побудову за стороною і прилеглими до неї кутами, зокрема).

Тому, запропонувавши учням зміст подібної задачі й отримавши відповідь на запитання (ΔABC = ΔA1B1C1), дістанемо протиріччя між результатом, який явно існує (рівність трикутників) та апаратом, що дозволяє аргументувати цю рівність (відповідної ознаки рівності трикутників ще не доведено). Це протиріччя і є основою мотивації діяльності учнів, а також поштовхом до цілепокладання.

IV. Актуалізація опорних знань

Виконання письмових вправ

За наведеним коротким записом сформулюйте розгорнуте твердження:

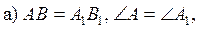
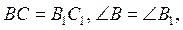тому ΔABC =Δ A1B1C1;

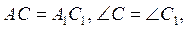
Б) AB = A1B1, AC = A1C1, тому ΔABC =Δ A1B1C1.

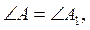
V. Засвоєння нових знань

План вивчення нового матеріалу

1°. Формулювання і доведення другої ознаки рівності трикутників.

2°. Приклади застосування другої ознаки рівності трикутників.

Методичний коментар

Методика викладання другої ознаки рівності трикутників аналогічна до викладення першої ознаки, тобто грунтується на уявленні про рівні фігури як ті, що співпадають при накладанні та на аксіомах відкладання відрізків та кутів.

Результатом роботи з вивчення нового матеріалу може стати схема 2, що подається в таблиці “Ознаки рівності трикутників”.

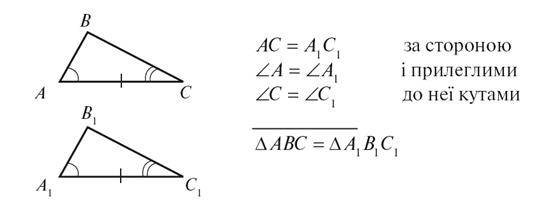
VI. Первинне усвідомлення нового матеріалу

Формуванню стійких умінь застосування другої ознаки рівності трикутників повинна передувати робота з вироблення вміння “бачити” “тріо”-сторону й прилеглі до неї кути. Тому на першому етапі приділяємо найбільше уваги саме завданням на розпізнавання елементів трикутників, названих у другій ознаці рівності трикутників.

Виконання усних вправ

1. У трикутниках ABC і 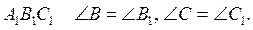Яку рівність необхідно додати до умови, щоб рівність даних трикутників можна було довести за другою ознакою?

2. У трикутниках ABC і 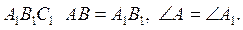Яку рівність необхідно додати до умови, щоб рівність даних трикутників можна було довести за другою ознакою?

3. Чи можна стверджувати, що ΔABC = ΔDEF, якщо AB = DE,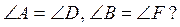

4. Якщо сторона й сума прилеглих до неї кутів одного трикутника відповідно дорівнюють стороні й сумі прилеглих до неї кутів другого трикутника, то такі трикутники рівні. Чи правильне це твердження?

Виконання письмових вправ

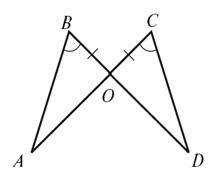
1. На рисунку 1 зображено пари рівних трикутників (рис. 1 а, б, в). Дайте обгрунтування рівності ΔABC =ΔA1B1C1 у кожному випадку.

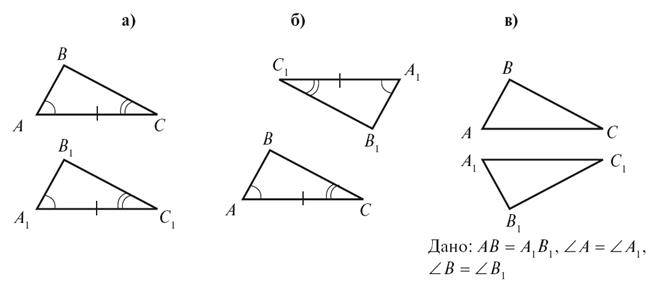
2. За даними рисунка 2 доведіть рівність трикутників ABC і A1B1C1.

3. На рисунку 3 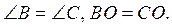Доведіть рівність трикутників AOB і DOC.

Під час розв’язування задач, в яких необхідно довести рівність трикутників і деякі рівності відповідних елементів задані явно, учні повинні знайти за умовою та властивостями геометричних фігур рівні елементи, яких бракує (наприклад, спільну сторону; рівність кутів на підставі означення бісектриси кута або властивості вертикальних кутів тощо).

VII. Підсумки уроку

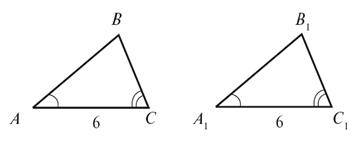
На рисунку 4 позначено дві пари відповідно рівних елементів Δ ABC і Δ A1B1C1. Яка пара елементів має бути рівною, щоб ΔABC =Δ A1B1C1:

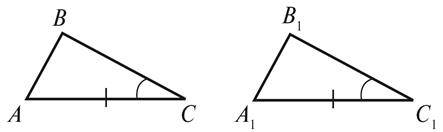
А) за першою ознакою рівності трикутників;

Б) за другою ознакою рівності трикутників?

VIII. Домашнє завдання

Вивчити формулювання та доведення другої ознаки рівності трикутників.

Усно виконати вправи.

1. У трикутниках ABC і KMN AB = KM, 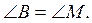Яку рівність необхідно додати до умови, щоб рівність можна було довести за другою ознакою?

2. Чи можна стверджувати, що ΔMNK = ΔDEF, якщо NK = EF, 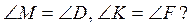Письмово розв’язати задачі.

1. Накресліть гострий кут A і проведіть його бісектрису AD.

А) Від променя DA по різні боки від прямої DA відкладіть рівні кути й позначте точки B і C – точки перетину сторін побудованих кутів зі сторонами кута A.

Б) Чи рівні трикутники ABD і ACD? Як це довести?

2. На рисунку 5 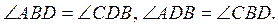Доведіть рівність трикутників ABD і CDB.