Електроємність
ФІЗИКА
Частина 3 ЕЛЕКТРИКА І МАГНЕТИЗМ
Розділ 8 ЕЛЕКТРИКА
8.7. Електроємність
Розглянемо спочатку відокремлений провідник, тобто такий, що міститься досить далеко від інших тіл. Якщо такому провіднику надавати різні заряди q1, q2,…, qn, то він заряджатиметься відповідно до потенціалів φ1, φ2,…, φn. Зі збільшенням заряду q зростатиме й потенціал φ, який змінюється так, що відношення заряду до потенціалу є величиною сталою:
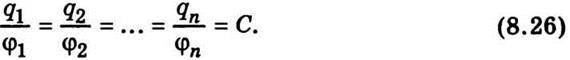
Це відношення називають електроємністю, або просто ємністю, провідника.
Електроємністю відокремленого провідника називають фізичну величину, яка чисельно дорівнює електричному заряду, що змінює його потенціал на одиницю.
За одиницю електроємності в СІ взято ємність конденсатора, напруга між обкладинками якого становить 1 В при заряді 1 Кл. Цю одиницю називають фарад:
Одиниця електроємності в системі СГСЕ дорівнює
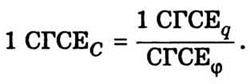
Неважко переконатися, що розмірність електроємності в системі СГСЕ збігається з розмірністю довжини. Тому одиницею електроємності в системі СГСЕ є сантиметр. Можна
Оскільки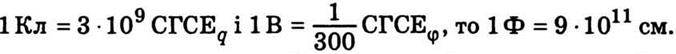 
На практиці використовують також інші одиниці електроємності:
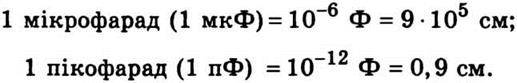
Якщо підрахувати електроємність Землі, вважаючи її провідною кулею радіуса 6400 км, то вона дорівнюватиме 711 мкФ.
Електроємність провідників залежить не від матеріалу, а від їхніх розмірів і форми, діелектричних властивостей навколишнього середовища, а також наявності поблизу провідника інших провідників.
Поняття електроємності можна застосувати і до системи провідників, найпростішою з яких є плоский конденсатор – система з двох металевих паралельних пластин, розділених шаром діелектри ка завтовшки d і однаково наелектризованих різнойменними зарядами.
При наданні обкладкам конденсатора зарядів +q і – q вони заряджатимуться до потенціалів φ1 і φ2. Електроємністю конденсатора називають відношення заряду q на одній із його обкладок до різниці потенціалів між обкладками:
Виходячи з теореми Остроградського – Гаусса, можна визначити напруженість однорідного електричного поля плоского конденсатора
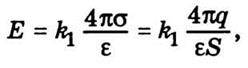
Де S – площа обкладок; σ = q/S – поверхнева густина зарядів на обкладках; k1 – коефіцієнт, що залежить від вибору одиниць виміру (в СІ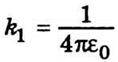 
). Для однорідного поля справедливе співвідношення (8.25), тому
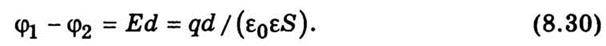
Підставивши цей вираз у (8.29), дістанемо формулу для обчислення електроємності плоского конденсатора
На практиці доводиться з’єднувати конденсатори в батареї. При паралельному з’єднанні конденсаторів їхня загальна ємність дорівнює сумі ємностей:
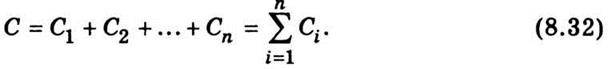
Ємність батареї послідовно з’єднаних конденсаторів визначають формулою
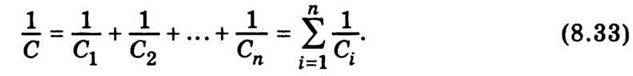
Отже, при паралельному з’єднанні конденсаторів ємності їх додаються, а при послідовному – додаються величини, обернені до їхніх ємностей.
Сферичний конденсатор складається з двох концентричних сферичних обкладок, розділених сферичним шаром діелектрика. Якщо внутрішній обкладці такого конденсатора надати заряд +q, то на зовнішній обкладці, що заземлена, наводитиметься заряд – q. Поле сферичного конденсатора зосереджене між його обкладками і є таким, ніби заряд зосереджений у центрі сфери. Тому потенціали обкладок обчислюють за такими формулами:
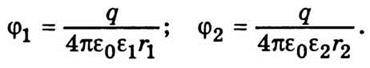
Тоді різниця потенціалів між обкладками
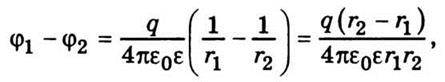
А електроємність сферичного конденсатора відповідно до формули (8.29)
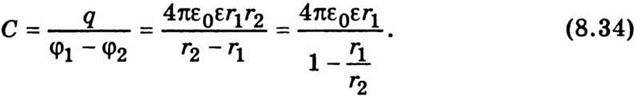
Якщо зовнішній радіус сферичного конденсатора набагато більший за внутрішній (r2 ” r1), то формула (8.34) спрощується і має такий вигляд
Якщо r2 -> ∞, то внутрішню обкладку сферичного конденсатора можна розглядати як відокремлену кулю, а формула (8.35) визначатиме її електроємність. У системі СГСЕ ємність відокремленої кулі вимірюється її радіусом r, якщо ε = 1.
(1 votes, average: 5.00 out of 5)
Loading...