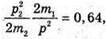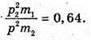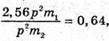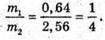ФІЗИКА АТОМНОГО ЯДРА ТА ЕЛЕМЕНТАРНИХ ЧАСТИНОК
Вправа 36
1.
Дано:
Mр = 1,00728 а. о. м. Mп = 1,00866 а. о. м. Mе = 0,00055 а. о. м. MН = 3,01605 а. о. м.
Е зв.- ? | Розв’язання: Енергія зв’язку ядра визначається як Е зв = λmс2, де Δm. – дефект маси ядра, який дорівнює різниці мас вільних частинок, що входить до складу ядра і маси спокою ядра. Δm = Zmр + Nmп – mя, Визначимо склад ядра: Нуклонів: А = 3. Протонів: Z = 1. Нейтронів: N = A – Z = 3 – 1 = 2. Масу ядра можна розрахувати як різницю Mя = mН – Zme. Тоді Δm = Zmр + Nmn – (mН – Zme) = Z(mp + mе) + Nmn – mH. Перевіримо одиниці фізичних величин: [Δm] = а. о. м. + а. о. м. + а. о. м. – а. о. м. = а. о. м.
Знайдемо числові значення: Δm = 1 х (1,00728 + 0,00055) + 2 х 1,00866 – 3,01605 = = 0,0091 (а. о. м.). Езв = 0,0091 х 931,5 = 48 (МеВ). Відповідь: енергія зв’язку ядра 8,48 МеВ. |
2.
Дано:
Mр = 1,00728 а. о. м. Mп = 1,00866 а. о. м. Me = 0,00055 а. о. м. MA1 = 26,98146 а. о. м.
Езв – | Розв’язання: Енергія зв’язку ядра визначається як: Езв = Δmс2, де Δm – дефект маси ядра, який дорівнює різниці мас вільних частинок, що входить до складу ядра і маси спокою ядра. Δm = Zmp+Nmn – mя. Визначимо склад ядра: Нуклонів: А = 27. Протонів: Z = 13. Нейтронів: N = А – Z = 27 – 13 = 14. Масу ядра можна розрахувати як різницю маси атоми і маси всіх електронів, що входять до складу атома: Mя = mA1 – Zme. Тоді Δm = Zmp + Nmп – (mA1 – Zme) = Z(mp + me) + Nmn – mA1. Перевіримо одиниці фізичних величин: [Δm] = а. о. м. + а. о. м. + а. о. м. – а. о. м. = а. о. м.
Знайдемо числові значення: Δm = 13 х (1,00728 + 0,00055) + 14 х 1,00866 – 26,98146 = = 0,24157 (а. о. м.). Езв = 0,24157 х 931,5 = 225 (МеВ). Відповідь: енергія зв’язку ядра 225 МеВ. |
3.
Дано:
Mр = 1,00728 а. о. м. Mn = 1,00866 а. о. м. Mе = 0,00055 а. о. м. MLi = 7,01601 а. о. м. Mо = 15,99491 а. о. м.
Eпит(Li) – ? Епит(О) – ? | Розв’язання: Енергія зв’язку, що припадає на один нуклон у ядрі, визначається як:
Енергію зв язку можна розрахувати як: Eзв (Li) = Δm(Li) х с2; Eзв (O) = Δ m(О) х с2, де Δm – дефект маси ядра, який дорівнює різниці мас вільних частинок, що входять до складу ядра, і маси спокою ядра: Δm = Zmp + Nmп – mя. Визначимо склад ядра Протонів: 2 = 3. Нейтронів: N = A – Z = 7 – 3 = 4. Визначимо склад ядра Протонів: Z = 8. Нейтронів: N = A – Z = 16 – 8 = 8. Масу ядра можна розрахувати як різницю маси атома і маси всіх електронів, що входять до складу атома: Mя(Li) = mLi – Zme; mя(О) = mO – Zme. Тоді: Δm(Li) = Zmp + Nmn – (mLi – Zme) = Z(mp + me) + Nmn – mLi; Δm(О) = Zmp + Nmn – (mO – Zme) = Z(m p + me) + Nmn – mO. Оскільки в ядрі Перевіримо одиниці фізичних величин: [Δm] = а. о. м. + а. о. м. + а. о. м. – а. о. м. = а. о. м.
Знайдемо числові значення: Δm(Li) = З х (1,00728 + 0,00055) + 4 х 1,00866 – 7,01601 = = 0,04212 (а. о. м.); Δm(О) = 8 х (1,00728 + 0,00055 + 1,00866) – 15,99491 = = 0,13701 (а. о. м.); Eзв(Li) = 0,04212 х 931,5 = 39,23 (МеВ); Eзв(O) = 0,13701 х 931,5 = 127,62 (МеВ);
Відповідь: питома енергія зв’язку ядра
|
4.
Дано: R. = 1,224 м й2 – 1,232 м m2- 238 а.ο.м.
“і-? | Розв’язання: · На заряджену частинку, що рухається в магнітному полі, діє сила Лоренца: F1 = Bq1v1, F2 = Bq2v2. Оскільки ізотопи мають однакову валентність, то їх заряди однакові: q2 = q2 = q. Сила Лоренца надає iонам доцентрового прискорення: F1 = m1a1, F2 = m2a2. Оскільки То Прирівняємо отримані вирази для сили Лоренца:
Перед тим як влетіти в магнітне поле, іони розганяються різницею потенціалів. Тоді їх кінетична енергія дорівнює:
Тоді: В результаті отримуємо: Звідси Перевіримо одиниці фізичних величин:
Знайдемо числові значення:
Відповідь: відношення мас ізотопів Урану 1,013, маса іонів легкого ізотопу 235 а. о. м. |
Вправа 37
1.
Дано:
| Розв’язання: Знайдемо частину радіоактивних ядер, що не розпалися із закону раді оактивного розпаду: N0 – початкова кількість ядер; N – кількість ядер, що залишилися у зразку через час t. Тоді: Виразимо отриманий результат в процентах: Частка радіоактивних ядер, що розпалися:
Відповідь: за половину періоду піврозпаду розпадеться 29 % ядер. |
2.
Дано:
Т = 27,8 діб T – ? | Розв’язання: Знайдемо частку ядер, що не розпалися:
Згідно з законом радіоактивного розпаду:
Отже, Перевіримо одиницю фізичної величини: [t] – доба. Знайдемо числове значення:
Відповідь: 80 % атомів розпадеться за 64,6 доби. |
3.
Дано: N = 6,4 X 108 T = 1 хв – 60 с А – ? | Розв’язання: Активність радіоактивного препарату – це кількість радіоактивних розпадів за одиницю часу: Перевіримо одиницю фізичної величини: Знайдемо числове значення:
Відповідь: А = 10,7 МБк. |
4.
Дано: А = 8,2 МБк = 8,2 х 106 Бк n = 25 х 108 T – ? | Розв’язання: Активність радіоактивного препарату – не кількість радіоактивних розпадів за одиницю часу: Тоді Перевіримо одиницю фізичної величини:
Знайдемо числове значення:
T = 5 хв 5 с. Відповідь: за 5 хв 5 с розпадається 25 х 108 ядер. |
5.
Дано: N0 = 1 млн. = 1 х 106 N’ = 175 000 = 0,175 х 106 t =1 доба = 86,4 х 103с Т – ? | Розв’язання: Згідно з законом радіоактивного розпаду: За одну добу в зразку залишиться N0 – N’ атомів. Тоді Перевіримо одиницю фізичної величини: [Т] = с. Знайдемо числове значення:
Відповідь: період піврозпаду Радону 3,11 х 105 с. |
6.
Дано: Т = 14,8 год = 53,3 х 103 с M = 1 мг = 10-6 кг T =10 год = 36 х 103 с
N’ – ? | Розв’язання: Кількість атомів, що розпалися, визначається як N’ = N0- N, де N0- початкова кількість атомів; N – кількість атомів, що не розпалися. Згідно з законом радіоактивного розпаду: Тоді Так як в 1 молі міститься кількість атомів, що дорівнює сталій Авогадро, то Отже, Перевіримо одиницю фізичної величини:
Знайдемо числове значення:
Відповідь: розпадеться 9,35 х 1018 атомів. |
7.
Дано: А = 20,7 МВк = 20,7 х 106 Бк Т = 7,1 х 108років = 22,4 х 1015 с
M – ? | Розв’язання: Оскільки період піврозпаду великий в порівнянні з часом спостереження, то активність можна Вважати сталою. Тоді: Так як в 1 молі міститься кількість атомів, що дорівнює сталій Авогадро, то кількість радіоактивних в препараті визначається як
Тоді: Перевіримо одиницю фізичної величини:
Знайдемо числове значення:
Відповідь: препарат містить 0,26 кг ізотопу |
8.
Дано: N = N0 = 0,015N0 Т = 5579 років T – ? | Розв’язання: Згідно з законом радіоактивного розпаду: Де N – кількість радіоактивних ядер ізотопу Карбону в знайденому зразку; N0- кількість радіоактивних ядер ізотопу Карбону у Свіжозрубаній деревині. Оскільки N – N0- 0,015N0 = N0 (1 – 0,015) = 0,985N0;
Отже, Перевіримо одиницю фізичної величини: [t] = рік. Знайдемо числове значення:
Відповідь: деревина була зрубана 122 роки тому. |
9.
Дано: M = 1 кг = 10-6 кг
M(Ро) = 209,9829 а. о. м. M(Рb) = 205,9744 а. о. м. M(Не) = 4,0026 а. о. м. T = 1 год = 3,6 х 103 с Т =138 діб =11,9 х106 с С = 3 · 108м/с ΔΤ – ? | Розв’язання: Температура в калориметрі піднімається за рахунок енергії, що виділяється під час радіоактивного розпаду: Q = CΔT. Калориметру передається енергія Q = N’W0, де N’ – кількість ядер, що розпалися; W0- енергія, що виділяється під час розпаду кожного Ядра. N′ = N0- N. Із закону радіоактивного розпаду: Оскільки t << Т, то Так як в 1 молі міститься кількість атомів, що дорівнює сталій Авогадро, то Знайдемо енергію виходу ядерної реакції: Із закону взаємозв’язку маси та енергії W0 = Δmс2, де Δm – різниця мас спокою частинок до і після реакції. Δm = m(Ро) – (m(Рb) + m(Не)). Знайдемо числове значення: Δm = 209,9829 – 205,9744 – 4,0026 = 0,0059 (а. о. м.). Δm = 0,0059 х 1,6605 х 10-27 = 9,8 х 10-30 (кг). В результаті: Перевіримо одиницю фізичної величини:
Знайдемо числове значення:
|
Вправа 38
1. 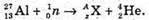
Згідно з законом збереження заряду: 13 = Z + 2, Z – 13 – 2 = 11.
Згідно з законом збереження масового числа: 27 + 1 = А + 4, А – 28 – 4 = 24.
Отже, 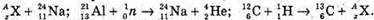
Згідно з законом збереження заряду: 6 + 1 = 6 + Z, Z = 7 – 6 = 1
Згідно з законом збереження масового числа: 12 + 1 = 13 + А, А = 13 – 13 = 0
Отже, 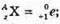
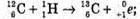
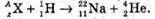
Згідно з законом збереження заряду: Z + 1 = 11 + 2, Z = 13 – 1 = 12.
Згідна з законом збереження масового числа: А + 1 = 22 + 4, А = 26 – 1 = 25
Отже, 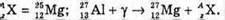
Згідно з законом збереження заряду: 13 = 12 + Z; Z = 13 – 12 = 1.
Згідно з законом збереження масового числа: 27 = 26 + А, А = 27 – 26 = 1.
Отже, 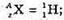
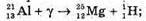
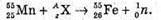
Згідно з законом збереження заряду: 25 + Z = 26, Z = 26 – 25 = 1.
Згідно з законом збереження масового числа: 55 + А = 55 + 1, А = 56 – 55 = 1.
Отже, 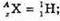
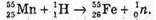
2. Якщо дефект мас Δm > 0, то енергія виділяється під час ядерної реакції.
А якщо дефект мас Δm < 0, то енергія поглинається під час ядерної реакції.
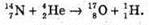
Дано: M(N) = 14,00307 а. о. м. M(Не) = 4,0026 а. о. м. M(О) = 16,99913 а. о. м. M(Н) = 1,00783 а. о. м. Δm – ? | Розв’язання: Дефект маси – це різниця між масами спокою частинок до та після реакції: Δm = m(N) + m(He) – m(O) – m(H). Am = 14,00307 + 4,0026 – 16,99913 – 1,00789 = = -0,00135 (а. о. м.). Оскільки Δm < 0, то енергія поглинається під час ядерної реакції |
Дано: M(Li) = 6,01513 а. о. м. M(Н) = 1,00783 а. о. м.
Δm – ? | Розв’язання: Дефект маси – це різниця між масами спокою частинок до та після реакції: Δm = 6,01513 + 1,00783 – 4,0026- 3,01602 = = 0,00434 (а. о. м.). Оскільки Δm > 0, то енергія виділяється під час ядерної реакції |
Дано: M(Li) = 7,01601 а. о. м M(He) = 4,0026 а. о. м. M(В) = 10,01294 а. о. м. M(п) = 1,00866 а. о. м. Δm – ? | Розв’язання: Дефект маси – це різниця між масами спокою частинок до та після реакції: Δm = m(Li) + m(Не) – m(B) – m(n}. Δm = 7,01601 + 4,0026 – 10,01294 – 1,00866 = = -0,00299 (а. о. м.) Оскільки Δm < 0, то енергія поглинається під час ядерної реакції |
3.
Дано: M(Li) = 7,01601 а. о. м M(Не) = 4,0026 а. о. м. M(В) = 10,01294 а. о. м. M(п) = 1,00866 а. о. м.
Wк – ? | Розв’язання: Для того, щоб відбулася ядерна реакція, необхідно, щоб різниця енергії спокою частинок до та після реакції була: ΔЕ ≥ 0. Тобто: (Li) + E(Не) + Wk= Е(В) + Е(п); Wk = Е(В)+Е(n)-E(Li)-Е(Не) = (m(В)+m(n)-m(Li)-m(Hе))с2. Перевіримо одиницю фізичної величини:
Знайдемо числове значення: Wк=(10,01294+1,00866-7,01601-4,0026)х931,5=2,785 (МеВ). Відповідь: α-частинка повинна мати мінімальну енергію 2,785 МеВ. |
4.
Дано: Е1 = Е – 0,64Е
M2 – ? | Розв’язання: Оскільки E1 = Е – 0,64E, то E1 = 0,36E, Е2 = 0,64 Е, Під час пружного зіткнення виконується закон збереження Імпульсу р = – р1 + р2, де Р – імпульс α-частинок до зіткнення, Р1 – імпульс α-частинок після зіткнення, Р2 – імпульс невідомої частинки після зіткнення. Імпульс пов’язаний з енергією співвідношенням:
Тоді: Оскільки р2 = р + p1 = р + 0,6 р = 1,6 р, то
В результаті m2 = 4m1. Перевіримо одиницю фізичної величини: [m] = а. о. м. Знайдемо числове значення: m2 = 4 х 4 = 16 (а. о. м.). Відповідь: α-частинка зітнулася з |
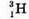
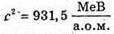
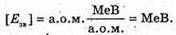
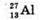
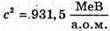
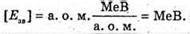
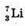
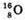
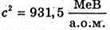
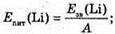
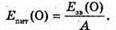
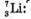 Нуклонів: А = 7.
Нуклонів: А = 7.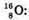 Нуклонів: А – 16.
Нуклонів: А – 16.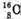 Z = N, то Δm(О) = Z(mp + me + mn) – mO.
Z = N, то Δm(О) = Z(mp + me + mn) – mO.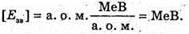
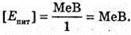
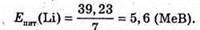
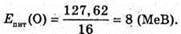
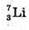 5,6 МеВ; а ядра
5,6 МеВ; а ядра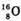 – 8 МеВ.
– 8 МеВ.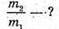
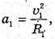
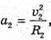
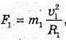
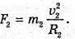
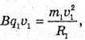
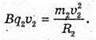
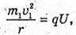
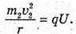
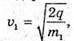
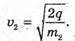
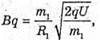
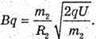
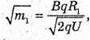
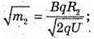
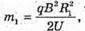
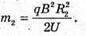
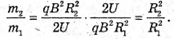
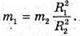
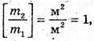
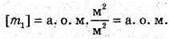
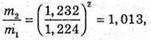
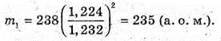
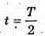
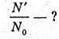
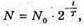 де
де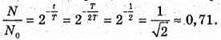
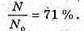
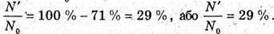
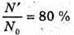
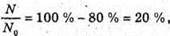 або
або 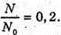
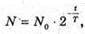
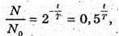
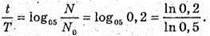
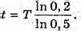
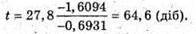
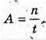
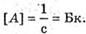
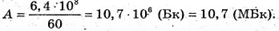
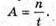
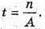
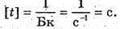
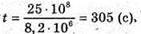
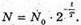
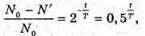 Отже,
Отже, 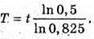
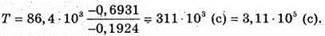
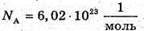
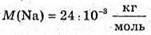
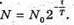
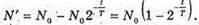
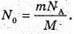
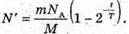
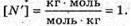
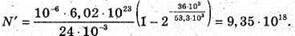
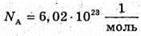
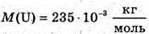
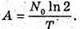
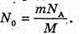
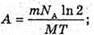
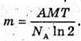
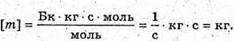
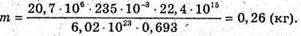
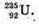
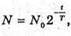
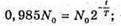
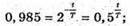
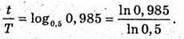
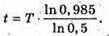
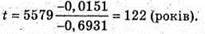
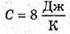
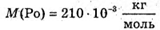
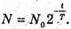
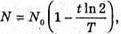
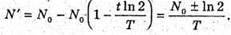
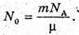 Отже,
Отже, 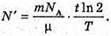
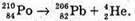
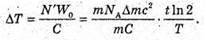
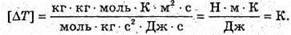
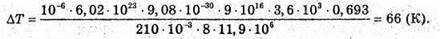
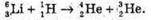
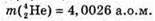
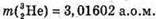
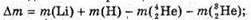
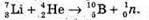
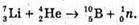
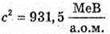
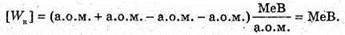
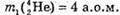
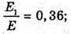
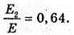
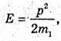
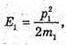
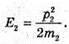
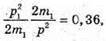
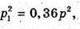 р1 = 0,6р,
р1 = 0,6р,