Формули скороченого множення
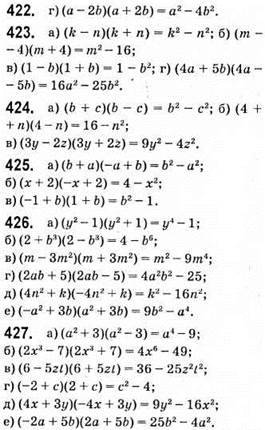


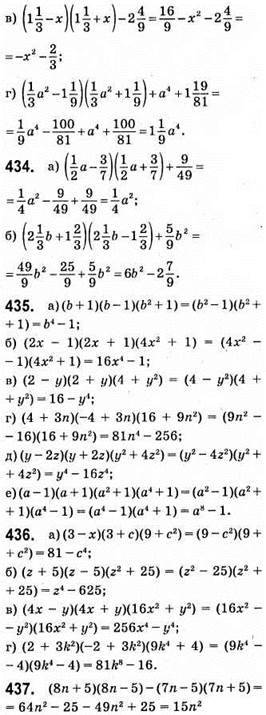
Ділиться на 15.
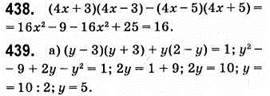
Відповідь: 5.
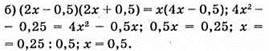
Відповідь: 0,5.
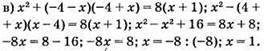
Відповідь: 1.
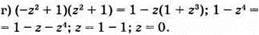
Відповідь: 0.
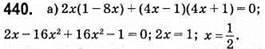
Відповідь: 1/2.
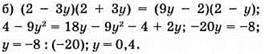
Відповідь: 0,4.
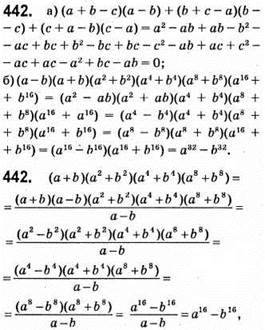
Якщо а – b = 1.
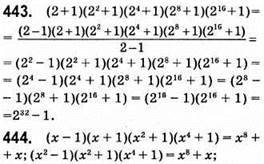
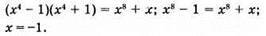
Відповідь: -1.
445. х – сторона
(x + 2) см – довжина прямокутника;
(x – 2) см – ширина прямокутника;
(x – 2)(x + 2) = (x2 – 4) см2 – площа прямокутника;
X2 > x2 – 4.
Відповідь: площа квадрата більша.
446. 1) 4000 • 0,08 = 320 (грн.);
2) 4000 + 320 = 4320 (грн.) – було у вкладника через рік;
3) 4752 – 4320 = 432 (грн.) – прибуток за другий рік;
4) 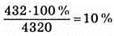 річних почав нараховувати банк після збільшення ставки.
річних почав нараховувати банк після збільшення ставки.
447. 1) 3,6 • 0,45 = 1,62 (кг) – міді у сплаві.
Нехай необхідно додати x кг міді, щоб отримати сплав, який містить 60 % міді.
(1,62 – x) кг міді у новому сплаві, маса якого (3,6 + x) кг.
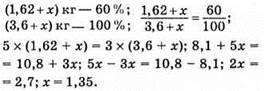
Відповідь: 1,35 кг міді треба додати.
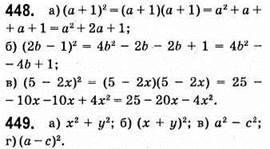
450. Один гном може мати 1, 2, 3, 4, 5, цукерок; всього 6 варіантів, а гномів сім, отже, деякі 2 громи можуть мати цукерок порівну.
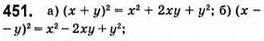
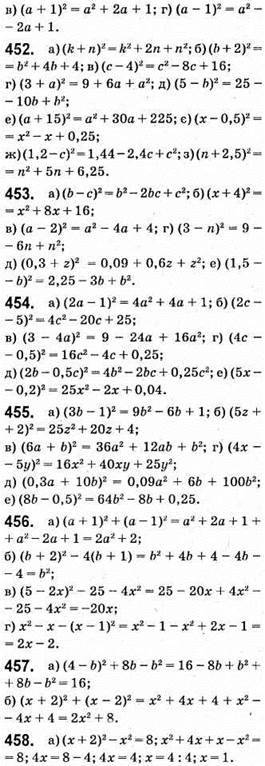
Відповідь: 1.
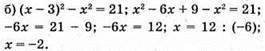
Відповідь: -2.
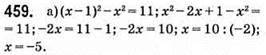
Відповідь: -5.
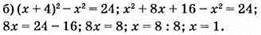
Відповідь: 1.


Тотожність доведено;
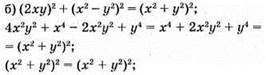
Тотожність доведено;
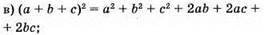
Тотожність доведено.
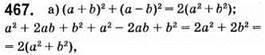
Тотожність доведено;
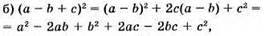
Тотожність доведено.
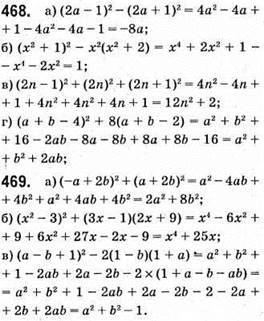
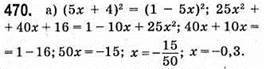
Відповідь: -0,3.
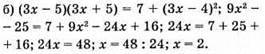
Відповідь: 2.
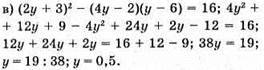
Відповідь: 0,5.
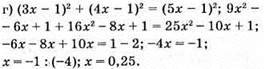
Відповідь: 0,25.
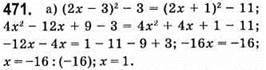
Відповідь: 1.
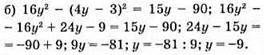
Відповідь: -9.
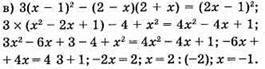
Відповідь: -1.
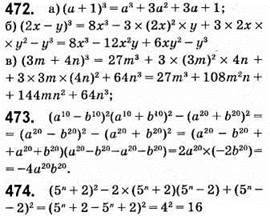
Ділиться на 16.
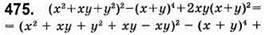
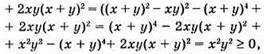
Набуває лише невід’ємних значень.
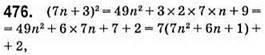
Дає в остачі 2.
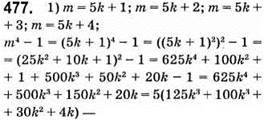
Ділиться на 5.
Аналогічно, 5k + 2; 5k + 3; 5k + 4 ділиться на 5.
478. Hi, не може.
479. 1) 80 ц : 0,1 = 800 (ц) – зберуть з усього поля;
2) 800 ц – 80 ц = 720 (ц) – зберуть з решти поля.
480.
Було | Стало | |
Перше число | 1,8х | 1,8х – 3,4 |
Друге число | X | Х + 2,2 |
Рівняння: 1,8х – 3,4 = х + 2,2; 1,8х – х = 3,4 + 2,2; 0,8х = 5,6; х = 5,6 : 0,8; х = 7. Друге число: 7, а перше число: 1,8х = 1,8 • 7 = 12,6.
Відповідь: 7; 12,6.
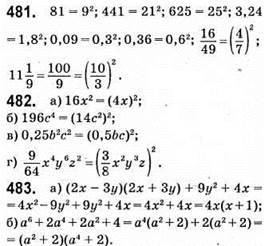
484. Зафарбуємо непарні стовпці дошки в чорний колір, а парні – у білий. Із чорної жук переповзе лише на білу, а з білої – лише на чорну. Якщо в деяких клітинках буде більше, ніж один жук, то порожніх клітинок буде не менше, ніж 7.
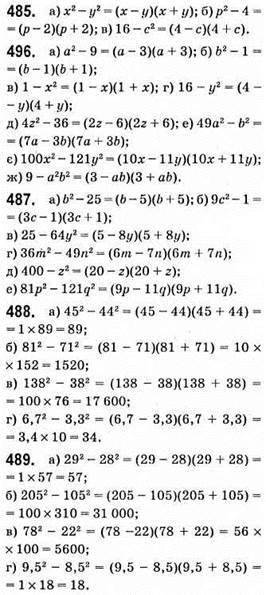
490. Якщо х = 42; у = 32, то х2 – у2 = (х – у)(х + у) = (42 – 32)(42 + 32) = 10 • 74 = 740.
Якщо х = 2,8; у = 7,2 то х2 – у2 = (х – у)(х + у) = (2,8 – 7,2)(2,8 + 7,2) = -4,4 • 10 = -44.
Якщо х = 54; y = -46, то х2 – y2 = (х – y)(х + у) = (54 + 46)(54 – 46) = 100 • 8 = 800.
491. m2 – n2 = (m – n)(m + n).
Якщо m = 116; n = 16, то (116 – 16)(116 + 16) = 100 • 132 = 13 200.
Якщо m = 5,7; n = -4,7, то (5,7 + 4,7)(5,7 – 4,7) = 10,7 • 1 = 10,7.
492. а) х2 – 4 = 0; (х – 2)(х + 2) = 0: х – 2 = 0 або x + 2 = 0; X = 2 або х = -2.
Відповідь: 2; -2.
Б) 25х2 – 16 = 0; (5x – 4)(5x + 4) = 0;
X = 4/5; x = -4/5.
Відповідь: 4/5; -4/5.
493. а) у2 – 36 = 0; (у – 6)(у + 6) = 0; у – 6 = 0 або у + 6 = 0; у = 6 або у = -6.
Відповідь: 6; -6.
Б) 100х2 – 49 = 0; (10х – 7)(10х + 7) = 0; 10х – 7 = 0 або 10х + 7 = 0; х = 7/10 або x = -7/10.
Відповідь: 7/10; -7/10.
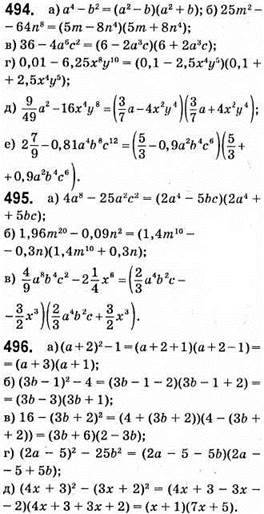
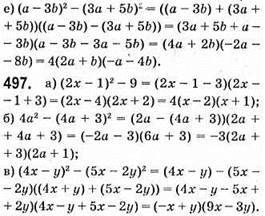
498. Якщо a = 3,28; b = 3,36, то а2 – 4b2 = (а – 2b)(а + 2b) = (3,28 – 2 • 3,36)(3,28 + 2 • 3,36) = (3,28 – 6,72) • (3,28 + 6,72) = -3,41 • 10 = -34,4.
Якщо 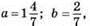 то а2 – 4b2 = (а – 2b)
то а2 – 4b2 = (а – 2b)
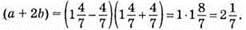
499. Якщо р = 2,3; q = -1,9, то 9р2 – q2 = (3р – q)(3р + q) = (3 • 2,3 + 1,9)(3 • 2,3 – 1,9) = (6,9 + 1,9)(6,9 – 1,9) = 8,8 • 5 = 44.
Якщо р = 3/14; q = 5/14, то 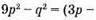
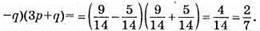
500. а) (х + 3)2 – 1 = 0; (х + 3 – 1)(х + 3 + 1) = 0; (х + 2)(х + 4) = 0; х + 2 = 0 або x + 4 = 0; х = -2; х = -4.
Відповідь; -2; -4.
Б) (5y – 2)2 – 9 = 0; (5у – 2 – 3)(5у – 2 + 3) = 0; (5р – 5)(5р + 2) = 0;
5у – 5 = 0 або 5у = -1; 5у = 5; y = -1/5; y = 1.
Відповідь: 1; -1/5.
В) (3z + 5)2 + 4z2 = 0;
3z + 5 – 2z = 0 або 3z + 5 + 2z = 0; z + 5 = 0; 5z + 5 = 0; z = -5; 5z = -5; z = -1.
Відповідь: -5; -1.
Г) (2х – 3)2 – (3х + 3)2 = 0;
2x – 3 + 3х + 3 = 0 або 2x – 3 – 3х – 3 = 0;
4х = 0; – х = 6; х = 0; х = -6.
Відповідь: -6; 0.
501. а) (2х – 5)2 – 1 = 0; (2х – 5 – 1)(2х – 5 + 1) = 0; (2х – 6)(2х – 4) = 0;
2х – 6 = 0 або 2х – 4 = 0;
Х = 3; х = 2.
Відповідь: 3; 2.
Б) (4y – 7)2 – (у + 2)2= 0; (4у – 7 + у + 2)(4у – 7 – у – 2) = 0;
5y – 5 = 0 або 3у – 9 = 0;
5y = 5; 3у = 9;
Y = 1; у = 3.
Відповідь: 1; 3.
502. а) 45752 – 14252 = (4575 – 1425)(4575 + 1425) = 3150 • 6000 – ділиться на 1000.
Б) 8432 – 2572 = (843 – 257)(843 + 257) = 586 • 1100 – ділиться на 100, 586 ділиться на 2; 1100 ділиться на 100.
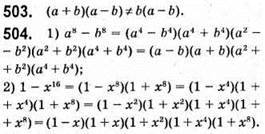
505. а) х4 – 16 = 0; (х2 – 4)(х2 + 4) = 0; (х – 2)(х + 2)(х2 + 4) = 0;
Х – 2 = 0 або х + 2 = 0 або х2 + 4 > 0;
Х = 2; х = -2.
Відповідь: 2; -2.
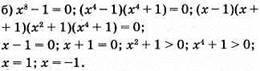
Відповідь: 1; -1.
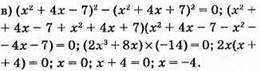
Відповідь: 0; -4.
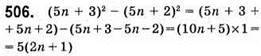
Ділиться на 5.
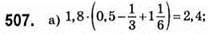
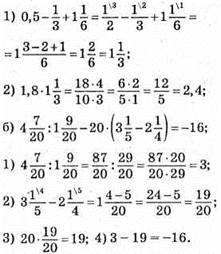
508. а) Батькові 36 років, синові 12 років. Через х років батькові (36 + х) років, синові (12 + х) років. Рівняння: 36 + х = (12 + х) • 2; 36 + х = 24 + 2х; х – 2х = 24 – 36; – х = -12; х = 12.
Відповідь: через 12 років.
Б) 36 – х = (12 – х) • 5; 36 – х = 60 – 4х; – х + 5х = 60 – 36; 4х = 24; х = 24 ; 4; х = 6.
Відповідь: 6 років.
509.
Швидкість | Час | Відстань | |
Автобус | Х км/год |
| 13/6х км |
Автомобіль | (х + 20) км/год | 3/2 год | 3/2(х + 20) км |
Рівняння: 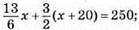 13х + 9х + 180 = 1500; 22х = 1320; х = 1320 : 22; х = 60.
13х + 9х + 180 = 1500; 22х = 1320; х = 1320 : 22; х = 60.
Швидкість автомобіля (60 + 20) км/год = 80 км/год.
Відповідь: 80 км/год.
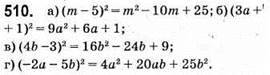
511. Якщо точки розмістити у вершинах рівностороннього трикутника зі стороною 1 см, то відстань між двома точками дорівнює 1 см.
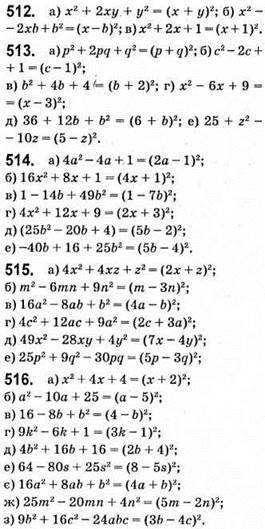
517. а) Якщо х = 12, то х2 – 4х + 4 = (х – 2)2 = (12 – 2)2 = 102 = 100.
Якщо х = 2,1, то х2 – 4х + 4 = (х – 2)2 = (2,1 – 2)2 = 0,12 = 0,01.
Якщо х = -18, то х2 – 4х + 4 = (х – 2)2 = (-18 – 2)2 = (-20)2 = 400.
Б) Якщо а = 7, то 9а2 – 6а + 1 = (3а – 1)2 = (3 • 7 – 1)2 = 202 = 400.
Якщо а = -33, то 9а2 – 6а + 1 = (3а – 1)2 = (3 • (-33) – 1)2 = (-100)2 = 10 000.
518. Якщо а = 4,5, то 4а2 + 4а + 1 = (2а + 1)2 = (2 • 4,5 + 1)2 = (9 + 1)2 = 102 = 100.
Якщо а = -5,5 то 4а2 + 4а + 1 = (2а + 1)2 = (2 • (-5,5) + 1)2 = (-11 + 1)2 = (-10)2 = 100.
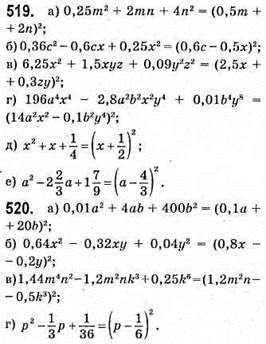
521. а) Якщо х = 1/7; у = 5/7, то 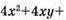
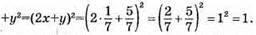
Б) Якщо а = 11,5; а = -7,5; а2 – 3а + 2,25 = (а – 1,5)2.
Якщо а = 11,5, то (11,5 – 1,5)2 = 102 = 100.
Якщо а = -7,5, то (-7,5 – 1,5)2 = (-9)2 = 81.
522. Якщо m = 2/3, n = 1/3, то 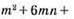
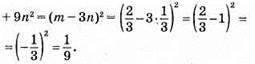
523. а) х2 – 8х + 16 = 0; (х – 4)2 = 0; х – 4 = 0; х = 4.
Відповідь: 4.
Б) у2 + 12у + 36 = 0; (у + 6)2 = 0; у + 6 = 0; у = -6.
Відповідь: -6.
524. а) z2 – 6z + 9 = 0; (z – 3)2 = 0; z – 3 = 0; z = 3.
Відповідь: 3.
Б) х2 + 10х + 25 = 0; (х + 5)2 = 0; х + 5 = 0; х = -5.
Відповідь: -5.

Відповідь: коренем є будь-яке число.
529.
Швидкість | Час | Відстань | |
Велосипедист | 2,5х км/год | 1 год | 2,5х км |
Пішохід | Х км/год | 2 год | 2х км |
Рівняння: 2,5х = 2х + 2,5: 2,5х – 2х = 2,5; 0,5х = 2,5; х = 2,5 : 0,5; х = 5.
5 км/год – швидкість пішохода.
Відповідь: 5 км/год.
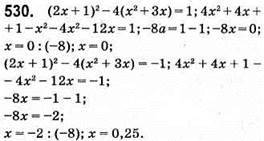
Відповідь: 0; 0,25.
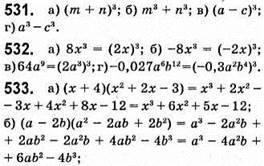
534. В обох чашках суміші порівну.
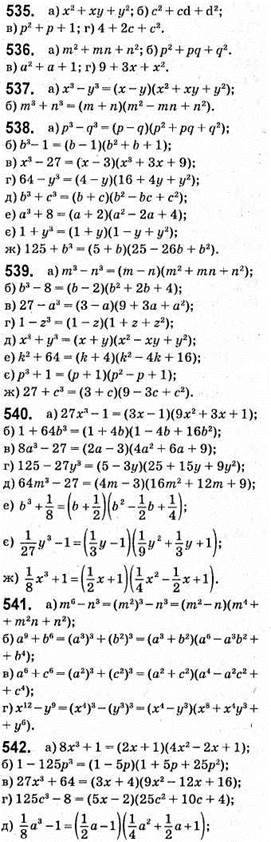
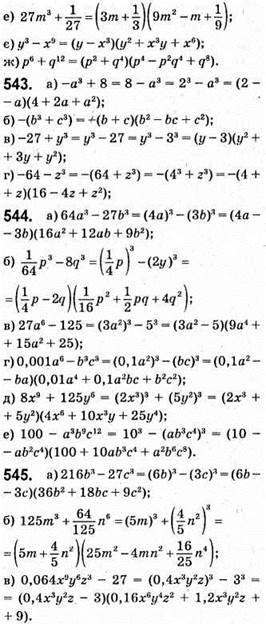
546. а) 9213- 8213 = (921 – 821)(9212 + 921 • 821 + 8212) = 100 • (9212 + 921 • 821 + 8212) ділиться на 100;
Б) 573 + 283 = (57 + 28)(572 – 57 • 28 + 282) = 85 • (572 – 57 • 28 + 282) ділиться на 85.
547. а) 273 + 373 = (27 + 37) • (272 – 27 • 37 + 372) = 64 • (272 – 27 • 37 + 372) – ділиться на 64;
Б) 753 – 463 = (75 – 46) • (752 + 75 • 46 + 462) = 29 • (752 + 75 • 46 + 462) – ділиться на 29.
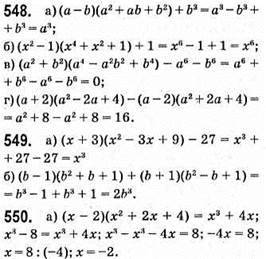
Відповідь: -2.
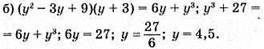
Відповідь: 4,5.
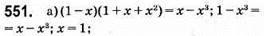
Відповідь: 1.
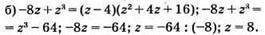
Відповідь: 8.
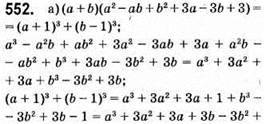
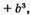 тотожність доведено;
тотожність доведено;
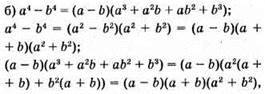
Тотожність доведено;
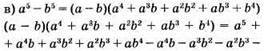
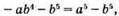 тотожність доведено;
тотожність доведено;
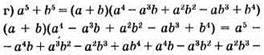
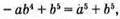 тотожність доведено;
тотожність доведено;
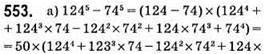
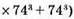 – ділиться на 50;
– ділиться на 50;
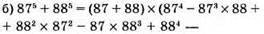
Ділиться на 175.
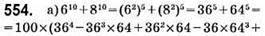
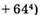 – ділиться на 100;
– ділиться на 100;
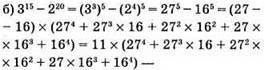
Ділиться на 11.
555. х і у – дані числа; 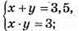
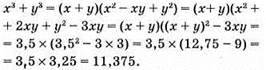
Відповідь: 11,375.
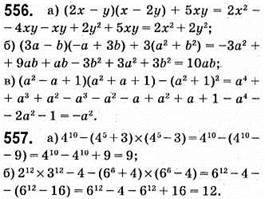
558. Нехай х годин – час, за який поїзд пройшов би відстань за планом, а фактично було витрачено (x – 1/6) години:
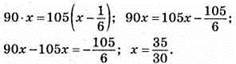
Відстань між пунктами А і В:
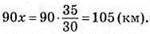
Відповідь: 105 км.
559. Нехай деякі два хлопчики не є братами, тоді вони не мають спільного брата і разом мають не менше 4 братів, а для цього необхідно 6 хлопчиків, а за умовою на майданчику є всього 5 хлопців. Отже, всі хлопчики є братами.
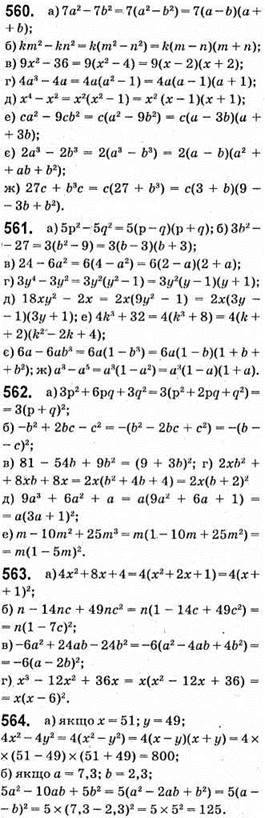
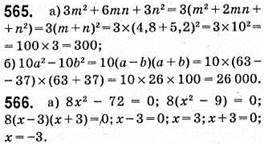
Відповідь: 3; -3.
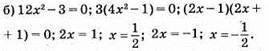
Відповідь: 1/2; -1/2.
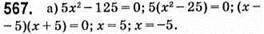
Відповідь: 5; -5.
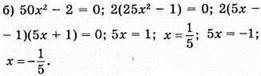
Відповідь: 1/5; -1/5.
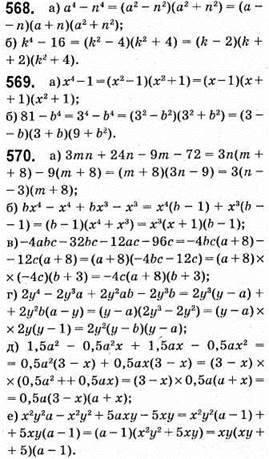

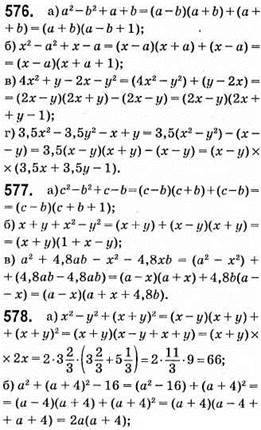
Якщо а = 96, то 2 • 96 • (96 + 4) = 192 • 100 = 19 200.
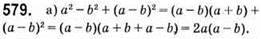
Якщо 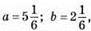 то
то 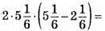
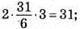
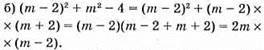
Якщо m = 102, то 2 • 102 • (102 – 2) = 20 400.
580. a) x3 – х = 0; х(х2 – 1) = 0; х(х – 1) • (х + 1) = 0; х = 0; або x – 1 = 0; х = 1; або х + 1 = 0; х = -1.
Відповідь: 0; 1; -1.
Б) 1,6у3 – 0,4у = 0; 0,4y(4у2 – 1) = 0; 0,4y = 0; у = 0; 2у – 1 = 0; у = 1; 2у + 1 = 0; y = -1/2.
Відповідь: 0; 1/2; -1/2.
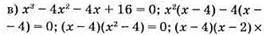
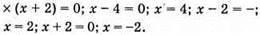
Відповідь: 4; 2; -2.
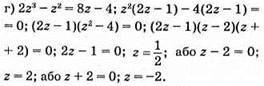
Відповідь: 1/2; 2; -2.
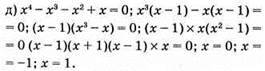
Відповідь: 0; -1; 1.
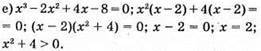
Відповідь: 2.
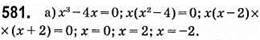
Відповідь: 0; 2; -2.
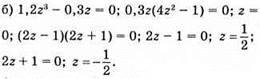
Відповідь: 0; 1/2; -1/2.
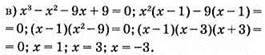
Відповідь: 1; 3; -3.
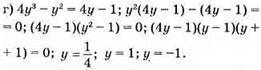
Відповідь: 1/4; 1; -1.
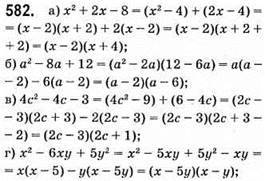
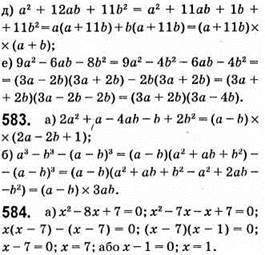
Відповідь: 7; 1.
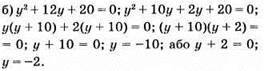
Відповідь: -10; -2.
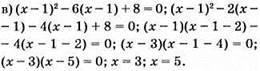
Відповідь: 3; 5.
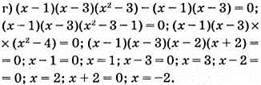
Відповідь: 1; 3; 2; -2.
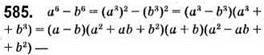
Тотожність доведено.
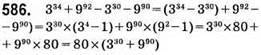
Ділиться на 80.
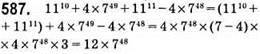
Ділиться на 12.
588. а3 + b2 = аb(а + 1); а3 + а2 = а2(а + 1); а3 + а2 = а3 + а2; якщо b = а.
Якщо b = а2; а3 + b4 = аа2(а + 1); а3 + b4 = а4 + а3.
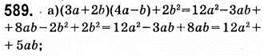
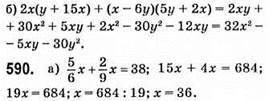
Відповідь: 36.
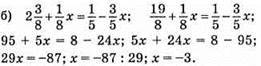
Відповідь: -3.
591. а) 2a(m + n); б) (а – 1)2 – b2с2.
592. 10% = 0,1. 4,2 • 0,1 = 0,42 (кг). На 0,42 кг більше міді, ніж цинку.
Нехай цинку у сплаві х кг, тоді міді (х + 0,42) кг.
Рівняння: х + х + 0,42 = 4,2; 2х + 0,42 = 4,2; 2х = 4,2 – 0,42; 2х = 3,78; х = 3,78 : 2; х = 1,89;
1,89 + 0,42 = 2,31 (кг) маса міді.
Відповідь: 2,31 кг.
593. Нехай олова було х кг, а міді було (2,2 – х) кг.
1,2х = 2,2 – х; 1,2х + х = 2,2; 2,2х = 2,2; х = 1.
Олова було 1 кг і міді було 1 кг. Перший сплав містив 50 % міді.
Відповідь: 50 %.
594. Ні, не може. Є вершина куба, що є ні початком, ні кінцем обходу. Скільки разів жук заповзе в цю вершину, стільки разів і виповзе з неї кожного разу по різних ребрах.
595. а) 7; б) 0; в) 3.
596. а) 7; б) 1; в) 5; а) х = 0; б) х = 2; в) х = -5.
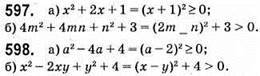
599. а) 2452 – 2362 = (245 – 236) • (236 + 245) = 9 • 481 – ділиться на 9;
Б) 4382 – 622 = (438 – 62) • (438 + 62) = 376 • 500 – ділиться на 500.
В) 523 – 363 = (52 – 36) • (522 + 52 • 36 + 362) = 16 • (522 + 52 • 36 + 362) – ділиться на 16;
Г) 753 + 253 = (75 + 25) • (752 – 75 • 25 + 252) = 100 • (752 – 75 • 25 + 252) – ділиться на 100.
600. а) 8112 – 7122 = (811 – 712) • (811 + 712) = 99 • 1529 – ділиться на 99;
Б) 483 – 193 = (48 – 19) • (482 + 48 • 19 + 192) – 29 • (482 + 48 • 19 + 192) – ділиться на 29.
601. а) 4х3 – 6×2 + 5х – 3.
Якщо x = 5, то 4 • 53 – 6 • 52+ 5 • 5 – 3 = 500 – 150 + 25 – 3 = 372;
Якщо х = 3,2, то 4 • 3,23 – 6 • 3,22 + 5 • 3,2 – 3 = 4 • 32,768 – 6 • 10,24 + 16 – 3 = 131,072 – 61,44 + 16 – 3 = 82,632.
Якщо x = -2,6, то 4 • (-2,6)3 – 6 • (-2,6)2 + 5 • (-2,6) – 3 = -4 • 17,576 – 6 • 6,76 – 13 – 3 = -70,304 – 40,56 – 16 = -126,864;
Б) 1,2×3 + 2,4×2 + 0,5х – 1;
Якщо x = 1,7, то 1,2 • (1,7)3 + 2,4 • (1,7)2 + 0,5 • 1,7 – 1 = 1,2 • 4,913 + 6,936 + 0,85 – 1 = 5,8956 + 6,936 + 0,85 – 1 = 12,6816;
В) х = 4,45 • х4 + 4 • х3 – 3,5х2 + 2х – 1,8 = 4,5 • 256 + 4 • 64 – 3,5 • 16 + 2 • 4 – 1,8 = 1152 + 256 – 56 + 8 – 1,8 = 1358,2.
602. а) якщо x = 2; 15×3 – 8×2 + 12х – 30 = 15 • 23 – 8 • 22 + 12 • 2 – 30 = 15 • 8 – 8 • 4 + 24 – 30 = 120 – 32 + 24 – 30 = 82;
Якщо х = 1,2, то 15 • 1,23 – 8 • 1,22 – 8 • 1,2 + 12 • 1,2 – 30 = 15 • 1,728 – 8 • 1,44 + 14,4 – 30 = 25,92 – 1152 + 14,4 – 30 = -1,2;
Якщо x = -4, то 15 • (-4)3 – 8 • (-4)2 + 12 • (-4) – 30 = 15 • (-64) – 8 • 16 – 48 – 30 = -960 – 128 – 48 – 30 = -1166;
Б) 2,4×4 – 7,2×3 – 3,3×2 + 4,5x = 2,4 • 34 – 7,2 • 33 – 3,3 • 32 + 4,5 • 3 = 2,4 • 81 – 7,2 • 27 – 3,3 • 9 + 4,5 • 3 = 194,4 – 194,4 – 29,7 + 13,5 = -16,2.
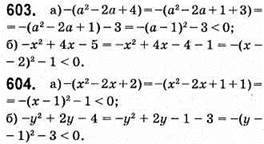
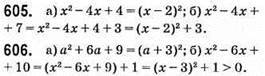
607. a) (n – 2)2 + 3n2 = n2 – 4n + 4 + 3n2 = 4n2 – 4n + 4 = 4(n2 – n + 1) – ділиться на 4;
Б) (n – 2)(2n – 7) – 2n2 – 3 = 2n2 – 7n – 4n + 14 – 2n2 = -11n + 11 = 11(-n + 1) – ділиться на 11.
608. (n + 2)2 – n(n – 2) + 2 = n2 + 4n + 4 – n2 + 2n + 2 = 6n + 6 = 6(n + 1) – ділиться на 6.
609. а) (n – 5)2 + (2n – 3)(2n + 8) = n2 – 10n + 25 + 4n2 + 16n – 6n – 24 = 5n2 + 1 – не ділиться на 5;
Б) (n – 3)(n2 – 3) – (n3 – 1) = n3 – 3n – 3n2 + 9 – n3 + 1 = -3n2 – 3n + 10 – не ділиться на 3.
610. (n + 3)2 – (n – 3)2 + 3 = n2 + 6n + 9 – n2 + 6n – 9 + 3 = 12n + 3 – не ділиться на 12.
611. 533 – 530 = 530 • (125 – 1) = 530 • 124 – ділиться на 124.
612. а) – х2 + 2х – 8 = -(x2 – 2х + 8) = -(x2 – 2х + 1 + 7) = -(х – 1)2 – 7;
-7, якщо х = 1.
Б) – а2 – 4а + 3 = -(а2 + 4а + 4 – 3) = -(а + 2)2 + 1.
7; якщо а = -2.
613. а2 – 4а + 7 = 1; а2 – 4а + 6 = 0; а2 – 4а + 4 + 2 = (а – 2)2 + 2 > 0. Ні, не може.
614. a) x2 – 7x + 12 = 0; x2 – 3x – 4x + 12 = 0; х(х – 3) – 4(х – 3) = 0; (х – 3)(х – 4) = 0; х – 3 = 0; х = 3 або х – 4 = 0; х = 4.
Відповідь: 3; 4.
Б) х2 – х – 12 = 0; х2 – 4х + 3х – 12 = 0; х • (х – 4) + 3(х – 4) = 0; (х – 4)(х + 3) = 0; х -4 = 0; х = 4; х + 3 = 0; х = -3.
Відповідь: 4; -3.
615. а) (х – 1)2 + (х – 3)2 = 0; коренів немає; (х – 1)2 > 0; (х – 3)2 > 0;
Б) (х2 – 1)2 + (х – 1)4 = 0; (х – 1)2(х + 1)2 + (х – 1)4 = 0; (х – 1)2((х + 1)2 + (х – 1)2) = 0; х – 1 = 0; х = 1.
Відповідь: 1.
616. а) 310 + 96= 310 + (32)6 = 310 + 312 = 310 • (1 + 32) = 310 • 10 – ділиться на 10;
Б) 220 + 225 – 222 = 220 • (1 + 25 – 22) = 220 • (1 + 32 – 4) = 220 • 29 – ділиться на 29.
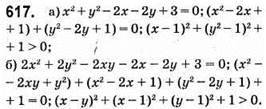
618. 4 = 2 + 2.
619. Р = (n + n – k) • 2, Р – периметр, n – довжина; (n – k) – довжина.
Р = (2n – k) • 2; S = n(n – k), S – площа.
620. x км/год – швидкість течії річки, (21 – х) км/год – швидкість проти течії річки.
(21 – х) • 1,2 = 7,2 • х; 25,2 – 1,2х = 7,2х; 8,4х = 25,2; х = 25,2 : 8,4; х = 3.
Відповідь: 3 км/год – швидкість течії річки.
621. Площа першої ділянки 2х га, площа другої ділянки 5х га, площа третьої ділянки (5х – 52) га. Рівняння:
2х + 3х + 5х – 52 = 568; 10х – 52 = 568; 10х – 620; х = 620 : 10; х = 62.
Площа першої ділянки 2 • 62 = 124 (га).
Площа другої ділянки 3 • 62 = 186 (га).
Площа третьої ділянки 258 га.
Відповідь: 124 га, 186 га, 258 га.
622. ах = 3, якщо а ≠ 0, рівняння має єдиний корінь. Якщо а = 0, це рівняння не має коренів.
623. Нехай таке розбиття на групи можливе, тоді в кожній групі сума чисел є парним числом, бо вона дорівнює подвоєному найбільшому числу групи, сума всіх заданих чисел є парним числом. Але серед даних чисел є 25 непарних чисел, отже, насправді сума всіх заданих чисел є непарною, тому це неможливо зробити.
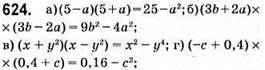
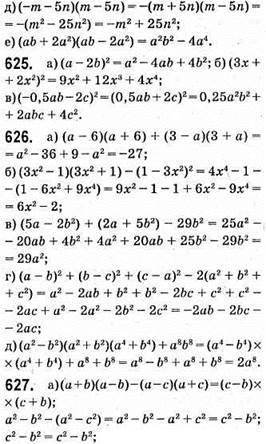
Тотожність доведено;
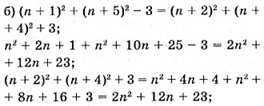
Тотожність доведено;
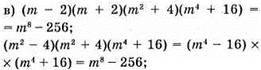
Тотожність доведено;
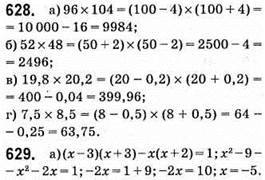
Відповідь: -5.
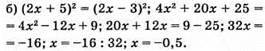
Відповідь: -0,5.
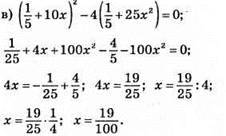
Відповідь: 19/100.
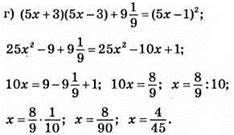
Відповідь: 4/45.
630. а) (2n + 1)(2n – 1) – (n + 1)2 – n – 1 = 4n2 – 1 – n2 – 2n – 1 – n – 1 = 3n2 -3n – 3 = 3(n2 – n – 1) – ділиться на 3;
Б) (2n + 7)(8n – 8) – (4n + 5)2 = 16n2 – 16n + 56n – 56 – 16n2 – 40n – 25 = -81 – не ділиться на 6.
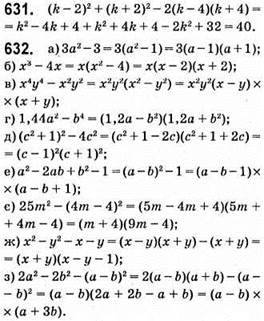
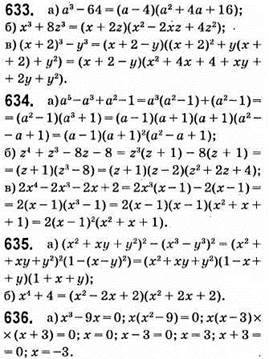
Відповідь: 0; 3; -3.
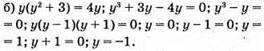
Відповідь: 0; 1; -1.
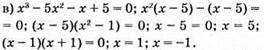
Відповідь: 5; 1; -1.
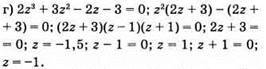
Відповідь: -1,5; 1; -1.
637. a) x2 – 4x + 4 + 2(x – 1)2 = 0; (x – 2)2 + 2(x – 1)2 = 0; коренів немає;
Б) (x2 + 1)2 + (x2 – x)2 = 1; (x2 + 1)2 + x2(x – 1)2 = 1.
Відповідь: x = 0.
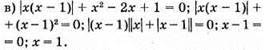
Відповідь: 1.
638. a) 4012 – 1992 = (401 – 199) • (401 + 199) = 600 • 202 – ділиться на 600;
Б) 853 – 483 = (85 – 48) • (852 + 85 • 48 + 482) = 37 • (852 + 85 • 48 + 482) – ділиться на 37;
В) 583 + 422 = (58 + 42) • (582 – 58 • 42 + 422) = 100 • (582 – 58 • 42 + 422) – ділиться на 100;
Г) 733 + 731 = 731 • (72 + 1) = 731 • 50 – ділиться на 50.
639. а) 825 – 6412 = 825 – 824 = 824 • (8 – 1) = 7 • 824 – ділиться на 7;
Б) 169 – 328 + 812= (24)9 – (25)8 + (23)12 = 236 – 240 + 236 = 236 • (1 – 24 + 1) = 236 • (-14) – ділиться на 7.
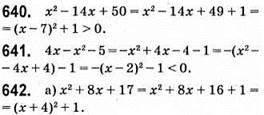
Відповідь: 1.
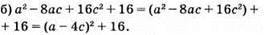
Відповідь: 16.
643. n, n + 1 – послідовні цілі числа; n2 – (n + 1)2 = n2 – n2 – 2n – 1 = -(2n + 1) – непарне число.
644. (2n + 1)2 – (2n + 3)2 = 4n2 + 4n + 1 – 4n2 – 12n – 9 = -8n – 8 = -8(n + 1) – ділиться на 8.
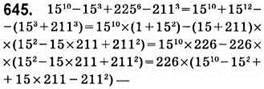
Ділиться на 226.
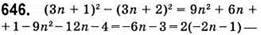
Ділиться на 3.
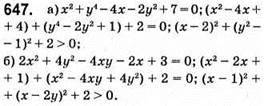
Завдання Для самоперевірки № 4
Рівень 1
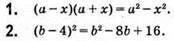
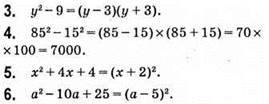
Рівень 2
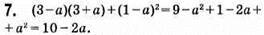
Якщо а = 0,5, то 10 – 2 • 0,5 = 10 – 1 = 9.
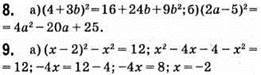
Відповідь: -2.
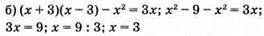
Відповідь: 3.
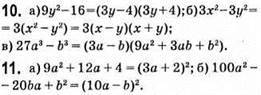
Рівень 3
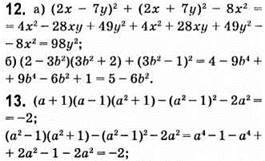
-2 = -2, тотожність доведено.
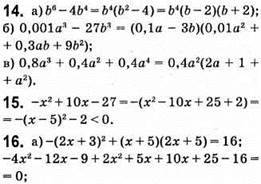
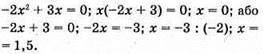
Відповідь: 0; 1,5.
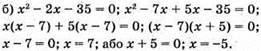
Відповідь: 7; -5.
Рівень 4
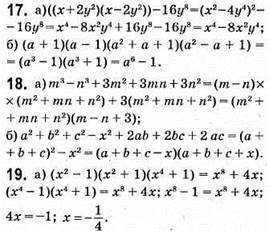
Відповідь: -1/4.
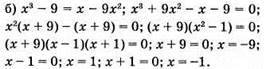
Відповідь: 1; -1; -9.
20. 5n + 3 – число n; 5n + 4 – число m.
(5n + 3)2 + (5n + 4)2 = 25n2 + 30n + 9 + 25n2 + 40n + 16 = 50n2 + 70n + 25 = 5(10n2 + 14n + 5) – ділиться на 5.
21. 4х2 + а2 – 4х + 1 = 4х2 – 4х + 1 + а2 = (2х – 1)2 + а2 > 0.
Многочлен набуває лише невід’ємних значень.
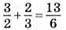 (год)
(год)