ГАРМОНІЧНІ ЕЛЕКТРОМАГНІТНІ КОЛИВАННЯ. ЧАСТОТА ВЛАСНИХ КОЛИВАНЬ КОНТУРУ
МЕХАНІЧНІ І ЕЛЕКТРОМАГНІТНІ КОЛИВАННЯ І ХВИЛІ
Розділ 3 Коливання і хвилі
§ 26. ГАРМОНІЧНІ ЕЛЕКТРОМАГНІТНІ КОЛИВАННЯ. ЧАСТОТА ВЛАСНИХ КОЛИВАНЬ КОНТУРУ
Розглянемо механізм виникнення коливань у коливальному контурі. Щоб отримати вільні коливання в механічній коливальній системі, необхідно надати цій системі енергію від зовнішнього джерела. У процесі коливань ця енергія періодично перетворюється з потенціальної в кінетичну, і навпаки. Щоб коливальний контур вивести зі стану електричної рівноваги, цій коливальній системі необхідно
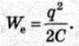
Якщо конденсатор замкнути на котушку індуктивності, то він почне розряджатися й у контурі виникне зростаючий з часом струм І. Отже, енергія електричного поля конденсатора буде зменшуватися, а енергія магнітного поля котушки – зростати.
Вважаючи,
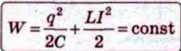
Тому що енергія на нагрівання провідників у такому коливальному контурі не витрачається. У момент часу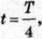 
коли конденсатор повністю розрядиться, енергія електричного поля зменшиться до нуля, а енергія магнітного поля, а отже, і сила струму досягне найбільшого значення (мал. 120, б). Починаючи з цього моменту часу сила струму у контурі буде зменшуватися, отже, почне слабшати магнітне поле котушки й індукований у ній струм, який тече (відповідно до правила Ленца) у тому ж напрямі, що й струм розрядки конденсатора. Конденсатор почне перезаряджатися, при цьому виникне електричне поле, яке намагатиметься послабити силу струму, який зрештою зменшиться до нуля, а заряд на обкладках конденсатора досягне максимуму (мал. 120, в). Далі ті ж процеси почнуть відбуватися в зворотному напрямі (мал. 120, г) і система до моменту часу t = Т повернеться в початковий стан (мал. 120, а). Після цього розглянутий цикл розрядки і зарядки конденсатора почне повторюватися.
Якби втрат енергії не було, то в контурі відбувалися б періодичні незатухаючі коливання, тобто періодично змінювалися (коливалися) б заряд q на обкладках конденсатора, напруга U на конденсаторі і сила струму І, який тече через котушку індуктивності.
Отже, у контурі виникають електричні коливання з періодом Т, причому протягом першої половини періоду струм тече в одному напрямі, протягом другої половини – у протилежному. Коливання супроводжуються перетвореннями енергій електричних і магнітних полів.
Електричні коливання у коливальному контурі можна порівняти з механічними коливаннями пружинного маятника (мал. 120), які супроводжуються взаємними перетвореннями потенціальної і кінетичної енергії маятника.
У даному випадку потенціальна енергія маятника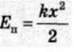 
аналогічна енергії електричного поля конденсатора 
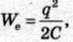кінетична енергія маятників
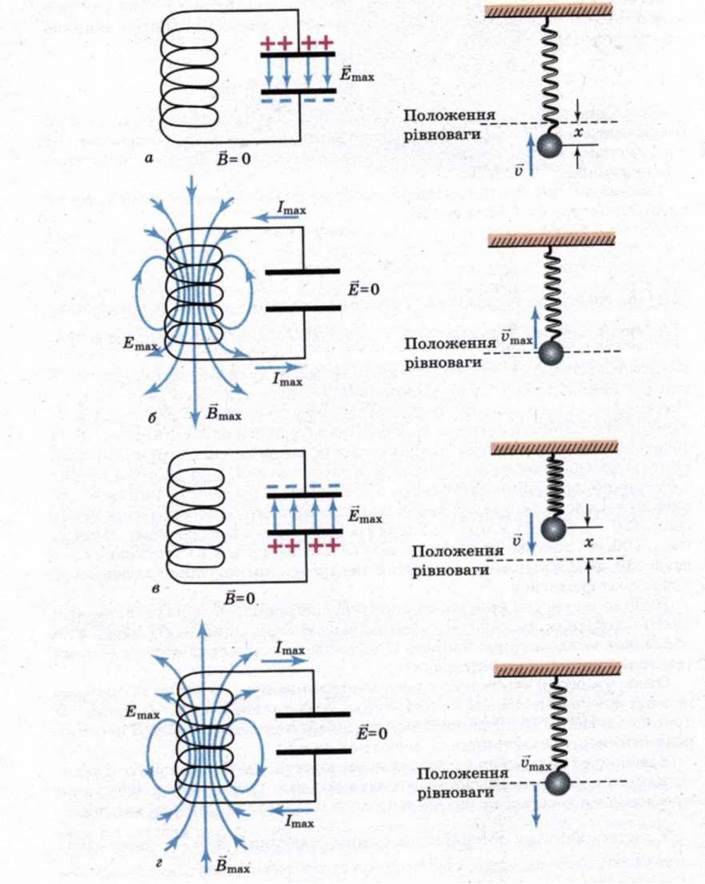
Мал. 120
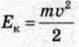– енергії магнітного поля котушки 
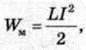а швидкість руху маятників – силі струму в контурі.
Роль інерції маятника буде зводитися до самоіндукції котушки, а роль сили тертя, яке діє на маятник – до опору контуру.
Перейдемо тепер до кількісної теорії процесів у коливальному контурі.
Наше завдання насамперед полягатиме у визначенні періоду (або частоти) вільних електричних коливань. Дійсно, виходячи з аналогії між вільними механічними і електричними коливаннями, можна відразу записати вираз для частоти і періоду вільних електричних коливань. Оскільки у формулі циклічної частоти вільних коливань тягарця на пружині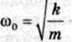 
величина к аналогічна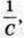 
Am – індуктивності L, то і частота вільних електричних коливань повинна дорівнювати
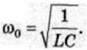
Для періоду вільних коливань у контурі можна записати
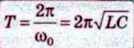
Формула Т = 2nLC називається формулою Томсона на честь англійського фізика, який її вперше вивів.
Отримані результати правильні. Проте вважати їх строго доведеними не можна. Треба показати, що рівняння, яке описує електричні коливання в контурі, з математичного боку не відрізняється від рівняння, яке описує вільні механічні коливання. Лише після цього можна з цілковитою певністю твердити, що механічні й електричні коливання підпорядковані одним й тим самим кількісним законам.
Як відомо, координата в механічних коливаннях, коли в початковий момент (t = 0) відхилення від положення рівноваги максимальне, змінюється з часом за гармонічним законом:
X = xmax cosω0t.
За таким самим законом змінюється з часом заряд конденсатора:
Де qmax – амплітуда коливань заряду. Гармонічно коливається і сила струму:
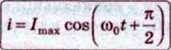
Де Imax =qmax ωo – амплітуда коливань сили струму. Коливання сили струму зміщені за фазою 
щодо коливань заряду (мал. 121), і, подібно до коливань
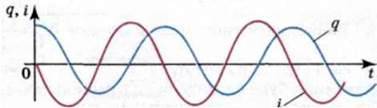
Мал. 121
Швидкості руху тягарця на пружині, випереджають за фазою на
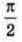коливання координати.
Дійсно, внаслідок енергетичних втрат коливання будуть затухаючими. Чим більший опір R, тим більшим буде період коливань. Коливання напруги будуть описуватись за таким законом:
(1 votes, average: 5.00 out of 5)
Loading...