Геометричні фігури, точка, пряма, промінь
Розділ 1. Елементарні геометричні фігури та їхні властивості
§ 1. Геометричні фігури, точка, пряма, промінь
1. 1) Прямій а належать точки А, В, С.
2) Прямій b належать точки Р i В.
3) Прямій а і прямій b належить точка В.
4) Точки А і С належать прямій а, але не належать прямій b.
5) Точки К і D не належать ні прямій а, ні прямій b.
2.
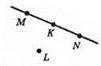
Пряма MN, К є MN, L ∉ MN.
3.
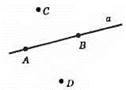
А є а, В є а, С ∉ a, D ∉ а.
4. 1) СА, CD, CM, CN – промені з початком у точці С;
2) BD і DC, DK і DL – пари доповняльних
5. 1) На рисунку зображені промені – NM, NP, NK, NF.
2) Серед променів, зображених на рисунку, є пара доповняльних променів – NM i NK.
6.

Можливі назви проведеної прямої – MN, MF, NF, FN, FM, NM.
7.
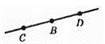
Пряму можна ще назвати: BD, DB, ВС, DC.
8. 1) Так, прямі m і СВ перетинаються.
2) Прямій m належать точки А і L.
3) Прямій ВС належать точки С, В і Q.
4) Ані прямій m, ані прямій ВС не належать точки К і D.
9.
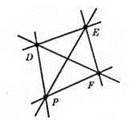
1) DP, DF, DE, ЕР, EF, PF.
2) Всього утворилося шість прямих.
3) Прямі розбивають площину на 16 частин.
10.
1) Утворилися прямі АС, AB, ВС.
2) Всього утворилося три прямих.
3) Прямі розбивають площину на 7 частин.
11.
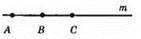
Точки В і С належать одному променю, якщо вони лежать по один бік від точки А.
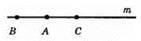
Точки В і С належать різним променям, якщо вони лежать по різні боки від точки А.
12. Три прямі на площині можуть перетинатися, це означає, що три точки будуть спільні між двома прямими. Отже, найменша кількість точок: 2017 + 2018 + 2019 – 3 = 6051.
Related posts:
- Промінь, пряма, площина Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 17. Промінь, пряма, площина Продовжимо відрізок АВ за допомогою лінійки за точку В (рис. 38). На рисунку таке продовження обмежене розмірами аркуша, але можна уявити, що ми продовжили відрізок необмежено. Якщо продовжити відрізок АВ за його кінець В необмежено, то одержимо промінь […]...
- Точка та прямі § 1. Найпростіші геометричні фігури та їхні властивості 1. Точка та прямі Практичні завдання 1. 2. Прямі ME, МК, ЕК, EM, КМ, КЕ. 3. Точка С належить прямій а, точка С належить прямій b. 4. Утворилося три прямих. 5. 6. Можна отримати три або одну точку перетину. 7. 1) 2) 3) Вправи 8. 1) Прямій […]...
- Площина. Пряма. Промінь Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 1. НАТУРАЛЬНІ ЧИСЛА 4. Площина. Пряма. Промінь Розміри вашого зошита не дають можливості будувати відрізки великої довжини. А уявіть собі, що аркуш зошита збільшився до розмірів стола, тенісного корту, навіть футбольного поля. Такий “аркуш” слугує прикладом частини площини. Площина нескінченна, тому її не можна зобразити. Цю […]...
- Площина. Пряма. Промінь УРОК 11 Тема. Площина. Пряма. Промінь Мета: закріпити знання, здобуті на попередньому уроці, про властивості прямої, площини і променя; розвивати просторову уяву учнів; перевірити засвоєння матеріалу з тем “Відрізок” та “Площина. Пряма. Промінь” під час виконання самостійної роботи. Тип уроку: засвоєння навичок та вмінь. Хід уроку I. Перевірка домашнього завдання та актуалізація опорних знань Усні […]...
- Вправи 1-49 1. А є ВС; В є АС. 2. А є с; В ∉ с. AB і с перетинаються в точці А. 3. Ці прямі мають тільки одну спільну точку А. 4. Точки В і С лежать по один бік від точки А. 5. а) Точка М лежить між L i N; Б) L і М […]...
- Вступ. Точка і пряма. Властивості точок і прямих Урок № 1 Тема. Вступ. Точка і пряма. Властивості точок і прямих Мета: ознайомити учнiв з предметом вивчення геометрiї, планiметрiї та iз поняттям найпростiших фiгур у геометрiї, домагатися вiд учнів свiдомого засвоєння термiнологiї, що описує взаємне розташування точок та прямих на площинi, формулювання основних властивостей розташування точок та прямих; виробити первиннi вмiння позначати точки та […]...
- Точки, прямі, промені Розділ 1. Найпростіші геометричні фігури та їх властивості § 1. Точки, прямі, промені 1. 1) Прямій m належать точки: В, D, N; 2) на прямій m не лежать точки: М, А, С. Відповідь: В є m, D є m, N є m, М ∉ m, A ∉ m, С ∉ m. 2. Відповідь: пряма АВ […]...
- ПРЯМА, ПРОМІНЬ, ВІДРІЗОК. ВИМІРЮВАННЯ ВІДРІЗКІВ РОЗДІЛ 1 ЛІЧБА, ВИМІРЮВАННЯ І ЧИСЛА § 2. ПРЯМА, ПРОМІНЬ, ВІДРІЗОК. ВИМІРЮВАННЯ ВІДРІЗКІВ На малюнку 7 ви бачите лінію високовольтної електропередачі, а на малюнку 8 – автомагістраль. Вони витягнуті, як струна, і ні початку, ні кінця їх не видно. Схематично кожну з них можна зобразити прямою лінією (мал. 9). Мал. 7 Мал. 8 Мал. 9 […]...
- Найпростіші геометричні фігури та їх властивості Урок № 14 Тема. Найпростіші геометричні фігури та їх властивості Мета: перевірити та оцінити рівень засвоєння знань та вмінь учнів з теми, передбачених програмою; виявити прогалини в знаннях та вміннях учнів для подальшого їх усунення. Тип уроку: перевірка та корекція знань, навичок та вмінь. ХІД УРОКУ І. Умова тематичної контрольної роботи Варіант 1 Початковий рівень […]...
- Переміщення та його властивості. Рівні фігури УРОК № 33 Тема. Переміщення та його властивості. Рівні фігури Мета уроку: формування поняття переміщення та рівних фігур; вивчення властивостей переміщення. Тип уроку: комбінований. Наочність і обладнання: таблиця “Перетворення фігур”. Рухи” [13]. Вимоги до рівня підготовки учнів: описують рівність фігур; будують фігури, у які переходять дані фігури при переміщеннях; формулюють властивості переміщення; застосовують вивчені означення […]...
- Промінь. Кут. Вимірювання кутів § 1. Найпростіші геометричні фігури та їхні властивості 3. Промінь. Кут. Вимірювання кутів Практичні завдання 49. Промені AB і АС – не доповняльні. Промінь AN – доповняльний до променя AB, а промінь AM – доповняльний до променя АС. На рисунку зображено промені АB, АС, AN, AM. 50. Промені AB і ВА не е доповняльними, оскільки […]...
- Відрізки та їх вимірювання Розділ 1. Найпростіші геометричні фігури та їх властивості § 2. Відрізки та їх вимірювання 28. 1) Кінці відрізка MN: М і N; внутрішні точки: А, О, В. 2) Кінці відрізка AN: A i N; внутрішні точки: О i B. 3) Кінці відрізка AB: А і В; внутрішня точка: О. 29. Утворилося три відрізки: AB, АС, […]...
- Геометричні фігури на площині Геометричні фігури на площині – Прямокутник – Квадрат 1 Назви множину. Розбий множину многокутників на підмножини. За якою ознакою це можна зробити? Розбий множину чотирикутників на дві підмножини. Розкажи, що ти знаєш про прямокутник. Розбий множину прямокутників на дві підмножини. Розкажи, що ти знаєш про квадрат. Якою фігурою є ABCD? KMNO? Назви пари протилежних сторін […]...
- Координатний промінь. Шкала Розділ 1 НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ. ГЕОМЕТРИЧНІ ФІГУРИ І ВЕЛИЧИНИ § 18. Координатний промінь. Шкала Накреслимо промінь ОХ горизонтально вправо від точки О і запишемо біля його початку число 0 (рис. 51). Дорівнює одиничному відрізку. Проти точки K запишемо число 1. Кажуть, що точка K відповідає числу 1, або число 1 зображено точкою […]...
- Многокутник – Геометричні фігури й величини Математика – Алгебра Геометричні фігури й величини Многокутник На рисунку ABCDE – п’ятикутник. A, B, С, D, E – вершини п’ятикутника; AB, BC, CD, DE, EA – сторони; AC, AD, BE, BD, CE – діагоналі. Окремі види многокутників На рисунках зображені окремі види многокутників. Прямокутник: – формула периметра. – формула площі. Квадрат: – формула периметра. […]...
- Геометричні фігури й величини Математика – Алгебра Геометричні фігури й величини На рисунках, поданих нижче, наведені деякі основні геометричні фігури; поруч даються назви й позначення. Відрізок AB (або BA). Промінь AB. Промінь BA. Пряма AB (або a). Ламана ABСDЕ. Промені AB і АС – доповняльні. Прямі а і b перетинаються. Промені АB і KN перетинаються, AB і CD не […]...
- Трикутник – Геометричні фігури й величини Математика – Алгебра Геометричні фігури й величини Трикутник На рисунку зображений трикутник зі сторонами a, b і c. – формула периметра трикутника. Сума всіх кутів довільного трикутника дорівнює . Кожний трикутник має принаймні два гострих кути. Види трикутників Види трикутників залежно від величини кутів (див. рисунок): а – гострокутний (усі кути гострі); б – тупокутний […]...
- Властивості руху Геометрія Рух Якщо кожну точку даної фігури змістити деяким чином, то дістанемо нову фігуру. Кажуть, що ця фігура утворюється перетворенням даної. Перетворення однієї фігури в іншу називається Рухом, якщо це перетворення зберігає відстань між точками. Властивості руху 1. Два рухи, виконані послідовно, дають знову рух. 2. Перетворення, обернене до руху, є рух. 3. Під час […]...
- Геометричні фігури на площині Мета: формувати уявлення про геометричні фігури Дидактичні задачі. Актуалізувати уміння розрізняти прямі, гострі і тупі кути; визначати ці кути у многокутнику; розбивати множини трикутників на підмножини за кутами: ті, що містять один прямий кут, один тупий кут, всі гострі кути; визначати трикутники, в яких всі стороні різної довжини, дві сторони рівні, три сторони рівні; класифікувати […]...
- КООРДИНАТНА ПРЯМА Розділ 4 РАЦІОНАЛЬНІ ЧИСЛА ТА ДІЇ З НИМИ § 22. КООРДИНАТНА ПРЯМА У п’ятому класі додатні числа і число 0 ви позначали на координатному промені (мал. 88). Продовжимо координатний промінь ОХ за його початок вліво. На добудованому промені нанесемо таку саму шкалу, як і на промені ОХ (мал. 89). Дістали координатну пряму. Точка О називається […]...
- Повторення. Геометричні фігури. Дроби Повторення. Геометричні фігури. Дроби 1 Розбий фігури на дві підмножини. Розбий плоскі фігури на дві підмножини. Назви елементи кожної підмножини. Яку найменшу кількість сторін може мати многокутник? Назви елементи многокутника. 2 Назви множину геометричних фігур. Розбий її на дві підмножини. Згадай, що ти знаєш про прямокутник; квадрат. 3 Запиши дроби, які позначають зафарбовану частину прямокутника. […]...
- Геометричні перетворення у просторі. Рухи 306. Пряма і площина відображуються на себе відносно будь-якої точки, що належить їм. 307. Два нерівні відрізки бути симетричними відносно деякої точки не можуть. 308. Відносно початку координат: Точці А(1; -3; 2) симетрична A1(-1; 3;-2); Точці В(-5; 0; 2) – B1(5; 0; -2); Точці С(3; -1; 0) – С1 (-3; 1; 0); Точці D(0; 0; […]...
- Відрізок. Вимірювання відрізків. Відстань між двома точками Розділ 1. Елементарні геометричні фігури та їхні властивості § 2. Відрізок. Вимірювання відрізків. Відстань між двома точками 13. На рисунку зображені відрізки: AB, AK, BK, ВМ. AK = 38 мм, MB = 12 мм. 14. На рисунку зображені відрізки: PC, PD, CD, PT. PC = 9 мм. PD = 31 MM. PT = 27 мм. […]...
- Геометричні фігури в просторі Мета: формувати уявлення про геометричні фігури у просторі Дидактичні задачі. Актуалізувати уявлення про просторові фігури: кулю, циліндр, конус, куб, піраміду, паралелепіпед; уміння визначати в оточуючому середовищі предмети, що мають форму даних фігур. Класифікувати геометричні фігури на просторові та плоскі; актуалізувати уявлення та поняття про плоскі фігури, що обмежують просторові фігури. Формувати уміння розв’язувати задачі з […]...
- ГЕОМЕТРИЧНІ ФІГУРИ В ГРАФІЧНОМУ РЕДАКТОРІ Розділ 3 ГРАФІЧНИЙ РЕДАКТОР 14. ГЕОМЕТРИЧНІ ФІГУРИ В ГРАФІЧНОМУ РЕДАКТОРІ Сьогодні ми продовжимо вчитися малювати в графічному редакторі Scratch. Розглянемо використання інструмента Прямокутник. Прямокутник можна намалювати зафарбований і не зафарбований. Щоб намалювати зафарбований прямокутник: 1. Вибери інструмент 2. Вибери значок зафарбованого прямокутника 3. Встанови вказівник у потрібне місце поля для малювання, натисни і утримуй кнопку […]...
- Прямокутний паралелепіпед – Геометричні фігури й величини Математика – Алгебра Геометричні фігури й величини Прямокутний паралелепіпед Прямокутний паралелепіпед (див. рисунок) має 8 вершин, 12 ребер, котрі можна розбити на 3 групи по 4 рівних, а також 6 граней (3 пари рівних між собою прямокутників). Площа поверхні прямокутного паралелепіпеда дорівнює сумі площ його граней: . Об’єм прямокутного паралелепіпеда . Коли , дістанемо Куб […]...
- Існування площини, яка проходить через дану пряму і дану точку УРОК 2 Тема. Існування площини, яка проходить через дану пряму і дану точку Мета уроку: вивчення теореми про існування площини, яка проходить через дану пряму і дану точку, що не лежить на прямій. Обладнання: стереометричний набір. Хід уроку І. Перевірка домашнього завдання 1. Фронтальна бесіда за контрольними запитаннями № 1, 2 §1 із підручника з […]...
- Тематичне оцінювання № 1 Урок 12 Тема. Тематичне оцінювання № 1 Мета уроку: перевірка навчальних досягнень учнів з тем “Вступ до стереометрії” та “Взаємне розміщення прямих у просторі”. Хід уроку Тематичне оцінювання № 1 можна провести, враховуючи результати виконання самостійної роботи на уроці № 6 та результати контрольної роботи. 1. Тематична контрольна робота № 1 Варіант А Варіант 1 […]...
- Шкала. Координатний промінь Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 1. НАТУРАЛЬНІ ЧИСЛА 5. Шкала. Координатний промінь За допомогою рівної дерев’яної рейки дві точки А і В можна сполучити відрізком (рис. 49). Однак цим примітивним інструментом виміряти довжину відрізка АВ не вдасться. Удосконалимо цей інструмент. Рис. 49 Рис. 50 На рейці через кожний сантиметр нанесемо штрихи. […]...
- Координатна пряма Урок № 6 3 Тема. Координатна пряма Мета: сформувати уявлення про зміст поняття координатна пряма, координата точки і виробити вміння за готовими рисунками визначати координати вказаних точок та будувати на координатній прямій точки із вказаними координатами. Тип уроку: засвоєння нових знань. Хід уроку І. Перевірка домашнього завдання @ Ігровий момент “Хто найуважніший?” Учитель читає текст, […]...