Існування площини, яка проходить через дану пряму і дану точку
УРОК 2
Тема. Існування площини, яка проходить через дану пряму і дану точку
Мета уроку: вивчення теореми про існування площини, яка проходить через дану пряму і дану точку, що не лежить на прямій.
Обладнання: стереометричний набір.
Хід уроку
І. Перевірка домашнього завдання
1. Фронтальна бесіда за контрольними запитаннями № 1, 2 §1 із підручника з використанням схеми “Аксіоми стереометрії”.
2. Математичний диктант.
Дано зображення тетраедра SABC (варіант 1 – рис. 8, варіант 2 – рис. 9).
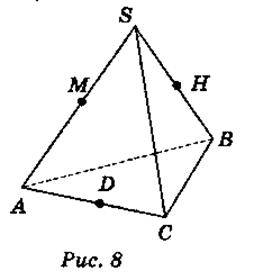
Користуючись зображенням, запишіть:
1) точки, які належать площині грані АВС; (2 бали)
2) точки, які не лежать у площині грані АВС; (2 бали)
3) спільні точки площин граней АВС і ABS; (2 бали)
4) пряму перетину площин граней АВС і SBC; (2 бали)
5) площину, яка проходить через прямі АВ і ВС; (2 бали)
6) площину, яка не містить жодної із прямих АВ і ВС. (2 бали)
3. Розв’язування задач № 1, 3 перевірити за записами з пропусками зробленими на дошці до початку уроку.
Розв’язання задачі № 1
Доведемо методом від супротивного. Припустимо, що АВ і СD…, тоді за аксіомою… через
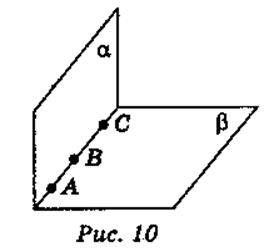
Нехай дві різні площини α і β мають спільні точки: … (рис.10). Згідно з аксіомою… площини… перетинаються по…, яка містить точки А, В, С.
Отже, точки… лежать на… перетину даних…, тобто на… прямій.
IІ. Сприйняття й усвідомлення нового матеріалу
Теорема про існуванню площини, яка проходить через дану пряму і дану точку
Один спосіб визначення площини в просторі відомий (аксиома С3): дві прямі, які перетинаються, визначають у просторі площину, і до того ж тільки одну.
Другий спосіб задання площини дає теорема:
Через пряму і точку, яка не належить їй, можна провести площину, і до того ж тільки одну.
Нехай АВ – дана пряма і С – точка, яка їй не належить (рис. 11).
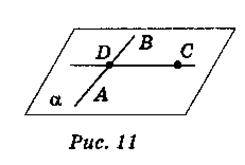
Доведення (існування площини).
Твердження | |
Візьмемо точку D, яка лежить на прямій АВ | |
Через точки D і С проведемо пряму DC | |
Через прямі АВ і DC проведемо площину α | С3 |
Доведення (єдність площини).
Доведемо від супротивного. Припустимо, що існує дві площини α і β, які проходять через пряму АВ і, точку С. За аксіомою С2 площини α і β перетинаються по прямій, якій належать А, В, С, що суперечить умові. Отже, площина, яка проходить через пряму і точку, що не належить прямій, єдина.
Завдання.
1. Вкажіть пряму і точку, за допомогою яких можна задати площину основи куба (див. рис. 2), тетраедра (див. рис. 3).
2. Дано зображення куба АВСDА1B1С1D1. Якій площині належать:
А) пряма АВ і точка D; б) пряма ВВ1 і точка С1; в) пряма АС і точка С1 ?
1. Доведіть, що через пряму і точку, яка лежить на прямій, можна провести площину.
2. Задача № 7 із підручника (с. 9).
3. Пряма а лежить в площині α. Доведіть, що через пряму а можна провести площину β, відмінну від α.
4. Дано десять точок, які не лежать в одній площині. Чи можуть дев’ять із них лежати на прямій? Відповідь обгрунтуйте.
5. Чи можна через точку О перетину двох даних прямих а і b провести третю пряму с, яка не лежить з прямими а і b в одній площині. Відповідь обгрунтуйте.
6. Задача № 4 із підручника (с. 9).
§1, п. 2; контрольне запитання № 3; задача № 6 (с. 9).
Запитання до класу
1) Скільки площин можна провести через пряму а і точку В, яка не належить прямій а?
2) Скільки площин можна провести через пряму а і точку А, яка лежить на прямій а?
3) Через пряму а і точку В можна провести дві різні площини. Як розташовані пряна а і точка B?
