Графік рівняння з двома змінними
УРОК № 28
Тема. Графік рівняння з двома змінними
Мета уроку: домогтися засвоєння учнями змісту: означення графіка рівняння з двома змінними; схеми дій для побудови графіка рівняння з двома змінними.
Виробити вміння: відтворювати зміст вивченого означення та алгоритму; застосовувати їх для розв’язування вправ на побудову графіків рівнянь з двома змінними.
Тип уроку: узагальнення та систематизація знань, вироблення вмінь.
Наочність та обладнання: опорний конспект № 18.
Хід уроку
I. Організаційний етап
Учитель
II. Перевірка домашнього завдання
Учитель перевіряє виконаний учнями аналіз тематичної контрольної роботи № 3.
III. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів
На цьому етапі уроку доречними є слова вчителя про те, що матеріал попереднього розділу “Функція та її властивості” може бути використаний не тільки для розв’язування квадратних нерівностей і завдань, що передбачають
IV. Актуалізація опорних знань та вмінь учнів
Усні вправи
1. Дано вирази:
А) х2 + у; б) ху + 3; в) у(х + 2).
Знайдіть значення кожного із даних виразів:
1) при х = -1, у = 2;
2) при x = -0,5, y = 0,4;
3) при x = –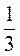 , у = 3.
, у = 3.
2. Дано функції:
А) у = – 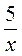 ; б) у = х2 – 2; в) у = 3х + 1; г) у = -2.
; б) у = х2 – 2; в) у = 3х + 1; г) у = -2.
Установіть відповідність між даними функціями та графіками:
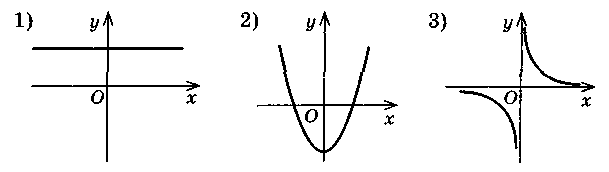
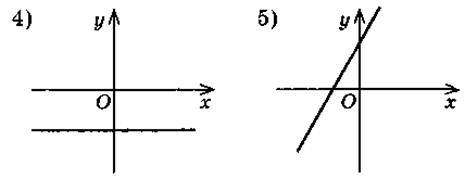
3. Виразіть одну змінну через іншу з рівності:
1) 4х – у = 1;
2) ху = 2;
3) х2 + у = 0;
4) х + ху = 2.
V. Формування знань
План вивчення нового матеріалу
1. Зміст поняття “рівняння з двома змінними” та супутніх понять.
2. Означення графіка рівняння з двома змінними. Степінь рівняння з двома змінними.
3. Схема дій при побудові графіка рівняння з двома змінними.
Опорний конспект № 18
Рівняння з двома змінними Приклади: х2 + у2 = 25, ху = 4, х + ху = 1. | ||||||
Супутні поняття | ||||||
1. Розв’язок рівняння з двома змінними х і у – це впорядкована пара (х; у), яка перетворює рівняння на правильну рівність. | ||||||
Наприклад, пара (2; 3) є розв’язком рівняння ху = 6, бо при х = 2 і y = 3 дане рівняння має вигляд 2 • 3 = 6, тобто утворюється правильна рівність. | ||||||
2. Степінь цілого рівняння з двома змінними р(х; у) = 0 визначається як степінь многочлена Р(х; у), якщо він зведений до стандартного вигляду. Наприклад, х2 + ху + у = 0 – рівняння другого степеня. | ||||||
Графік рівняння з двома змінними х і у – це множина точок координатної площини з координатами (х; у), де пара (х; у) є розв’язком даного рівняння з двома змінними. | ||||||
Як побудувати графік рівняння з двома змінними 1. Якщо рівняння можна звести до вигляду (х – a)2 + (y – b)2 = R2, де а, b – довільні числа, a R > 0, то графіком цього рівняння буде коло з центром (а; b) і радіусом R. | ||||||
2. В інших випадках (якщо немає модуля) виражаємо у через х і будуємо графік утвореної функції y = f(x). | ||||||
Приклад. Побудуємо графік рівняння: 1) 2x – 3у = 6; 2) х2 + у2 = 9; 3) ху = 4. | ||||||
Розв’язання (див. рисунок) | ||||||
1) 2х – 3у = 6 | ||||||
Х | 0 | 3 |
| |||
Y | -2 | 0 | ||||
2) х2 + у2 = 9 = 32 – рівняння кола з центром (0;0) і радіусом 3. 3) ху = 4; у = | ||||||
Х | -4 | -2 | -1 | 1 | 2 | 4 |
У | -1 | -2 | -4 | 4 | 2 | 1 |
Методичний коментар
Основна частина навчального матеріалу уроку – це відомості та вміння, які учні вже отримали при вивченні алгебри в попередніх класах. На даному уроці проводяться переважно повторення, узагальнення та систематизація навчального матеріалу.
VI. Формування вмінь
Усні вправи
1. Чи є розв’язком рівняння х2 + у = 10 пара чисел:
1) x = 3, у = 1;
2) (-2; 6)?
2. Чи належать точки A(-2; 3); B(0; 0); С(3; 0) графіку рівняння:
1) ху = -6;
2) х2 – у = 9;
3) х2 + у2 = 9?
3. Визначте степінь рівняння:
1) ху – 2у = 5;
2) х2 – у = 2;
3) х2 + 3у2 = 0.
4. Що є графіком рівняння:
1) х2 + у2 = 4;
2) (x – 1)2 + (y + 3)2 = 9;
3) х = 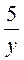 ; 4) х = 3у – 1?
; 4) х = 3у – 1?
Письмові вправи
Для реалізації дидактичної мети уроку слід розв’язати вправи такого змісту:
1) визначити, чи є дана пара чисел розв’язком рівняння з двома змінними;
2) побудувати графік рівняння з двома змінними;
3) знайти кілька розв’язків рівняння з двома змінними аналітично та за графіком рівняння з двома змінними;
4) на повторення: розв’язати системи лінійних рівнянь з двома змінними.
Методичний коментар
Для кращого засвоєння учнями змісту матеріалу уроку рекомендується при виконанні відповідних вправ неодноразово повторювати означення розв’язку рівняння з двома змінними, графіка рівняння з двома змінними та алгоритм побудови графіка рівняння з двома змінними (див. опорний конспект № 18).
VII. Підсумки уроку
Контрольні запитання
1. Наведіть приклади рівнянь з двома змінними різних видів.
2. Що називається розв’язком рівняння з двома змінними? Для кожного з наведених у п. 1 рівнянь знайдіть хоча б один із розв’язків (якщо вони є).
3. Наведіть приклади рівнянь з двома змінними, графіками яких є:
1) коло;
2) пряма;
3) гіпербола;
4) парабола.
4. Яку загальну властивість має будь-яка точка графіка даного рівняння з двома змінними?
VIII. Домашнє завдання
1. Вивчити означення понять, розглянутих на уроці.
2. Розв’язати вправи на побудову графіків рівнянь з двома змінними.
3. Повторити способи розв’язування систем лінійних рівнянь з двома змінними (за довідником для 7 класу); розв’язати системи лінійних рівнянь з двома змінними різними способами.
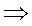 у =
у = 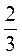 Х – 2 – лінійна функція.
Х – 2 – лінійна функція.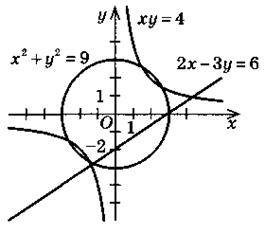
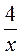 – обернена пропорційність.
– обернена пропорційність.