Головна ⇒ 📌Довідник з математики ⇒ Границя функції
Границя функції
Математика – Алгебра
Границя
Границя функції
Нехай функція 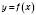 визначена на проміжку
визначена на проміжку 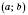 (можливо, що
(можливо, що 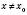 ). Число A називається границею функції
). Число A називається границею функції 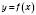 у точці
у точці 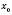 , якщо для будь-якого числа
, якщо для будь-якого числа 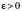 існує таке число
існує таке число 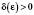 , що для всіх
, що для всіх 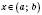 ,
, 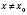 і таких, що
і таких, що 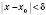 , виконується нерівність
, виконується нерівність 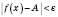
Позначення:
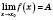 , або
, або 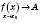 .
.Нехай
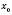 – внутрішня точка проміжку
– внутрішня точка проміжку 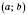 .
.Функція
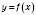 називається нескінченно малою в точці
називається нескінченно малою в точці 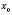 , якщо для будь-якого числа
, якщо для будь-якого числа 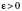 існує число
існує число 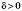 таке, що для всіх
таке, що для всіх 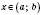
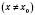 , які задовольняють нерівність
, які задовольняють нерівність 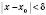 , виконується нерівність
, виконується нерівність 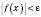 .
.Теорема 1. Сума (різниця) двох нескінченно
Функція
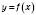 називається Обмеженою на проміжку
називається Обмеженою на проміжку 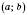 , якщо існує таке число
, якщо існує таке число 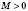 , що для всіх значень x із цього проміжку виконується нерівність
, що для всіх значень x із цього проміжку виконується нерівність 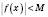 .
.Теорема 2. Добуток нескінченно малої функції та обмеженої функції є функцією нескінченно малою в даній точці.
Теорема 3. Щоб функція
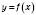 у точці
у точці 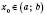 мала границею число A, необхідно і достатньо, щоб різниця
мала границею число A, необхідно і достатньо, щоб різниця 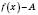 була нескінченно малою функцією в цій точці.
була нескінченно малою функцією в цій точці.Можна ввести означення, еквівалентне даному раніше. Число A називається границею функції
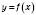 в точці
в точці 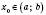 , якщо різниця між цією функцією та числом A є нескінченно малою функцією в цій точці.
, якщо різниця між цією функцією та числом A є нескінченно малою функцією в цій точці.Related posts:
- Границя числової послідовності Математика – Алгебра Границя Границя числової послідовності Число a називається Границею послідовності,, …, , …, якщо для будь-якого додатного числа існує таке натуральне число , що для всіх виконується нерівність . Позначеня: , або . Послідовність , , 2, … називається Нескінченно малою, якщо для будь-якого додатного числа ε існує натуральне число N таке, що […]...
- Властивості нескінченно малих послідовностей Математика – Алгебра Границя Властивості нескінченно малих послідовностей Теорема 1. Алгебраїчна сума скінченного числа нескінченно малих послідовностей є нескінченно малою послідовністю. Послідовність називається Обмеженою, якщо існує таке число , що для всіх значень 2, … виконується нерівність . Теорема 2. Добуток нескінченно малої числової послідовності та обмеженої послідовності є нескінченно малою послідовністю. Послідовність називається Нескінченно […]...
- Неперервність функції в точці Математика – Алгебра Границя Неперервність функції в точці Нехай функція визначена на проміжку і точка є внутрішньою точкою цього проміжку. Функція називається Неперервною в точці, якщо існує границя функції в цій точці й вона дорівнює значенню функції в точці . Нехай функція визначена в усіх точках деякого проміжку . Візьмемо дві довільні точки з цього […]...
- Поняття первісної функції – Інтеграл і його застосування Математика – Алгебра Інтеграл і його застосування Поняття первісної функції Первісною для даної функції на заданому проміжку називається така функція , що для всіх . Операція знаходження первісної F для даної функції називається Інтегруванням. Теорема 1. Будь-яка неперервна на відрізку функція має первісну функцію. Лема. Якщо на деякому проміжку, то на цьому проміжку, де C […]...
- Арифметичні операції над диференційовними функціями Математика – Алгебра Похідна Арифметичні операції над диференційовними функціями Теорема 1. Якщо функції і в точці мають похідні, то функція в цій точці також має похідну, яка дорівнює . Теорема 2. Якщо функції і в точці мають похідні, то в цій точці функція також має похідну, яка дорівнює . Наслідок. Якщо функція має похідну в […]...
- Обернені функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Обернені функції Дві функції називаються оберненими, якщо вони виражають ту саму залежність між змінними величинами, але в одній з них за аргумент прийнято х, а за функцію – у, в іншій – навпаки, тобто за аргумент прийнято у, а за функцію – х. Функції у = f(x) […]...
- Основні властивості неперервних функцій Математика – Алгебра Границя Основні властивості неперервних функцій Теорема 1. Якщо функції і є неперервними в точці , то в цій точці будуть неперервними і функції , . Теорема 2. Якщо і є неперервними в точці і , то в точці є неперервною також і функція . Зверніть увагу: всі дробово-раціональні функції і основні тригонометричні […]...
- Схема дослідження – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Функцією (або функціональною залежністю) називається закон, за яким кожному значенню незалежної змінної х з деякої множини чисел, що називається областю визначення функції, ставиться у відповідність тільки одне певне значення величини у. Графіком функції називається множина всіх точок координатної площини з координатами (х, у), такими, при яких абсциса […]...
- Застосування похідної Математика – Алгебра Похідна Застосування похідної Нехай функція визначена на проміжку і . Функція називається Зростаючою в точці, якщо існує інтервал , де , який міститься у проміжку і є таким, що для всіх x з інтервалу і для всіх x з інтервалу . Функція називається Спадною в точці, якщо існує інтервал , який міститься […]...
- Числові функції. Зростаючі і спадні, парні і непарні функції УРОК 1 Тема. Числові функції. Зростаючі і спадні, парні і непарні функції Мета уроку: Узагальнення і систематизація знань учнів про числові функції (область визначення і область значення функцій, зростаючі і спадні функції, парні і непарні функції). І. Мотивація навчання Процеси реального світу тісно пов’язані між. собою. Серед різноманіття явищ вчені виділили такі, у яких взаємозв’язок […]...
- Первісна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Первісна функція Первісною для даної функції y = f(x) на проміжку (а; b) називається така функція F(x), похідна якої для всіх х (а;b), що дорівнює f(x): F'(x) = f(x). Загальний вигляд первісної F(x) + C, де С – довільне стале число. Теорема. Будь-яка неперервна на функція y = f(x) […]...
- Похідна Математика – Алгебра Похідна Похідною функції в точці називається границя відношення приросту функції до приросту аргументу за умови, що границя існує, а приріст аргументу прямує до нуля, тобто . Функція в точці називається Диференційовною, якщо в цій точці вона має похідну . Якщо функція є диференційовною в кожній точці деякого інтервалу , то вона називається […]...
- Числові функції Математика – Алгебра Числові функції Залежність змінної y від змінної x називається Функцією, якщо кожному значенню x відповідає єдине значення y. x називається Аргументом, або Незалежною змінною, y – Залежною змінною, або Функцією від x. Позначення: , і т. д. Множина значень, яких набуває незалежна змінна x, називається областю визначення функції. Позначення: , і т. […]...
- Властивості функцій – Функції та графіки Математика – Алгебра Функції та графіки Властивості функцій Функція називається Зростаючою на деякому проміжку, якщо більшому значенню аргументу із цього проміжку відповідає більше значення функції. Функція називається Спадною на деякому проміжку, якщо більшому значенню аргументу із цього проміжку відповідає менше значення функції. Якщо функція зростає (спадає) на всій області визначення, її називають зростаючою (спадною). Приклади […]...
- Зростаючі й спадні функції Математика – Алгебра Числові функції Зростаючі й спадні функції Функція називається Зростаючою на деякому інтервалі, якщо для будь-яких двох значень аргументу з цього інтервалу більшому значенню аргументу відповідає більше значення функції. Функція називається Спадною На деякому інтервалі, якщо для будь-яких значень аргументу з цього інтервалу більшому значенню аргументу відповідає менше значення функції. Приклади 1) y […]...
- Екстремуми функції Математика – Алгебра Числові функції Екстремуми функції Точку x0 називають Точкою мінімуму функції, а саме число – Мінімумом функції, якщо існує інтервал , , на якому функція визначена і для всіх із цього інтервалу. Точку називають Точкою максимуму функції, а саме число – Максимумом функції, якщо існує інтервал , , на якому функція визначена і […]...
- Функції. Властивості функції: нулі функції, проміжки знакосталості, зростання і спадання функції УРОК № 19 Тема. Функції. Властивості функції: нулі функції, проміжки знакосталості, зростання і спадання функції Мета уроку: закріпити знання учнів про означення поняття нулів функції, проміжків знакосталості, функції, що зростає або спадає на проміжку, а також про способи відшукання названих характеристик функції у випадках, якщо функція задана графічно або аналітично. Закріпити вміння учнів виконувати дії […]...
- Обернені тригонометричні функції: у = arcsin х, у = arccos х УРОК 18 Тема. Обернені тригонометричні функції: у = arcsin х, у = arccos х Мета уроку: вивчення властивостей обернених тригонометричних функцій: у = arcsin х, у = arccos х. І. Перевірка домашнього завдання Математичний диктант. Закінчіть математичні твердження: 1. Функція, яка набуває кожного свого значення в єдиній точці області визначення називається… 2. Оберненою до функцій […]...
- Функції Математика – Алгебра Функції Функціональною відповідністю, або Функцією, називають таку відповідність між двома змінними, коли кожному значенню однієї змінної відповідає одне значення другої змінної. Першу змінну називають Незалежною, або Аргументом функції, а другу – Залежною, або Функцією від першої змінної. Усі значення, які приймає незалежна змінна, утворюють Область визначення функції. Записують: , де x – […]...
- Обернені тригонометричні функції: у = arctg x, у = arcctg x УРОК 19 Тема. Обернені тригонометричні функції: у = arctg x, у = arcctg x Мета уроку: вивчення властивостей обернених тригонометричних функцій: у = arctg х і у = arcctg x. І. Перевірка домашнього завдання 1. Фронтальна бесіда з класом за питаннями 6, 7, 9-12, до “Запитання і завдання для повторення” розділу II. 2. Самостійна робота. […]...
- Обернені тригонометричні функції – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ У = sin x 0; π/2 π/2 π/2; π π π; 3π/2 3π/2 3π/2; 2π 2π M A X П E P E Т И Н И M I N П E P E Т И Н И У = cos x 0; π/2 π/2 π/2; π π π; […]...
- Числові та лінійні нерівності УРОК № 60 Тема. Числові та лінійні нерівності Тестові завдання 1. Яку подвійну нерівність задовольняє множина чисел, поданих на рисунку? А) -4 < x < 8; Б) -4 < х < 8; В) -4 < х < 8; Г) -4 < х < 8. 2. Відомо, що х < у. Яка з наведених нерівностей є […]...
- Правила знаходження первісних – ПРОПОРЦІЇ. ВІДСОТКИ Формули й таблиці МАТЕМАТИКА ПРОПОРЦІЇ. ВІДСОТКИ Правила знаходження первісних Правило 1. Якщо функції у = f(x) і у = g(x) мають на числовому проміжку X первісні, відповідно у = F(x) й у = G(x), то і сума функцій у = f(x) + g(x) має на проміжку X первісну у= =F(x) + G(x). (Первісна суми дорівнює […]...
- Степеневі функції – ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Формули й таблиці МАТЕМАТИКА ФУНКЦІЇ ТА ЇХНІ ВЛАСТИВОСТІ Степеневі функції Графіки функції є параболами степеня n Графіки функції є гіперболами Функція y = ах, де а > 0, а ≠ 1, називається показниковою функцією з основою а. Приклад 0 < а < 1 Y = (1/2)x А > 1 Y = 2х Область визначення Х […]...
- Основні теореми про границі функцій Математика – Алгебра Границя Основні теореми про границі функцій Теорема 1. Якщо функції і в точці мають границі, то сума і добуток цих функцій також мають у цій точці границю, причому ; . Теорема 2. Якщо функції і в точці мають границі й , то й функція має в цій точці границю, яка дорівнює . […]...
- Графік функції. Графічний спосіб задання функції Розділ 2. ФУНКЦІЇ & 20. Графік функції. Графічний спосіб задання функції У 6 класі ми вже розглядали графік залежності між двома величинами. Розглянемо поняття графіка функції. Приклад 1. Нехай дано функцію у = + 3, де -2 ≤ х ≤ 3. Знайдемо значення цієї функції для цілих значень аргументу і занесемо результати в таблицю: Х […]...
- Парність функції Математика – Алгебра Числові функції Парність функції Функція називається Парною, якщо: 1) ; 2) . У парних функцій протилежним значенням аргументу відповідають рівні значення функції. Графік парної функції симетричний відносно осі Oy. Функція називається Непарною, якщо: 1) ; 2) . У непарних функцій протилежним значенням аргументу відповідають протилежні значення функції. Графік непарної функції симетричний відносно […]...
- Підсумковий урок з теми “Функції. Властивості функції. Функція у = ах2+bx+c. Розв’язування квадратних нерівностей” УРОК № 26 Тема. Підсумковий урок з теми “Функції. Властивості функції. Функція у = ах 2 + b х + С. Розв’язування квадратних нерівностей” Мета уроку: повторити, систематизувати й узагальнити знання та вміння учнів щодо змісту вивчених у розділі “Функція та її властивості” понять і схем розв’язування типових задач шляхом складання загальних алгоритмів розв’язування задач. […]...
- Функція. Область визначення функції. Область значень функції Урок № 60 Тема. Функція. Область визначення функції. Область значень функції Мета: закріпити термінологію, відпрацювати навички роботи з поняттями функції; відпрацювати навички роботи із функцією, заданою формулою і таблично; знаходити функції аргументу, області визначення функції. Тип уроку: засвоєння вмінь та навичок. Хід уроку I. Організаційний момент (традиційно) II. Перевірка домашнього завдання @ Оскільки основна частина […]...
- Похідна функція – ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Формули й таблиці МАТЕМАТИКА ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ Похідна функція – визначення похідної функції. Рівняння дотичної до графіка функції y = f(x) у точці М(х0,у0): – кутовий коефіцієнт дотичної....