Коливання. Гармонічні коливання
ФІЗИКА
Частина 1 МЕХАНІКА
Розділ 2 ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ
2.17. Коливання. Гармонічні коливання
Коливаннями називають процеси, що відбуваються з точним або наближеним повторенням станів системи. Така повторюваність властива, наприклад, коливанням маятника годинника, коливанням струни, зміні напруги між обкладками конденсатора в контурі радіоприймача тощо.
Залежно від фізичної природи процесу, що повторюється, розрізняють коливання механічні, електромеханічні, електромагнітні тощо. У цьому розділі розглянемо механічні
Залежно від характеру дії на систему, що коливається, розрізняють вільні (або власні), вимушені, параметричні коливання та автоколивання. Найпростішими є гармонічні коливання, тобто такі, коли значення, що змінюється при коливаннях (наприклад, відхилення маятника від положення рівноваги), змінюється з часом за законом синуса або косинуса. Цей різновид коливань важливо розглянути з таких причин: по-перше, коливання, що спостерігаються в природі й техніці, за своїм характером наближаються до гармонічних, а, по-друге, періодичні процеси іншої форми (з іншою залежністю від часу) можна уявити як накладання
Розглянемо гармонічні коливання суто тематично. Нехай точка В (рис. 2.10) рухається по колу радіуса а зі сталою кутовою швидкістю ω. Простежимо за рухом точки С (проекції В на вертикальну вісь). У момент часу t = 0 радіус ОB займав положення ОА. Тоді в момент часу t радіус ОВ повернеться з початкового положення ОА на кут φ. Зміщення х точки С, що дорівнює відрізку ОС, визначається так:

Кут φ називають фазою коливання точки С.
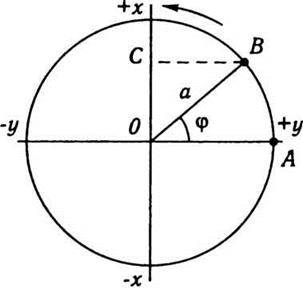
Рис. 2.10
Якщо 2π є довжиною дуги повного кола в кутових одиницях, а Т – час обходу точкою В повного кола, то кутова швидкість дорівнює

Величину ω також називають коловою, або циклічною, частотою. Звідси неважко виразити фазу φ через ω:

Підставивши це значення фази в рівняння (2.59), дістанемо
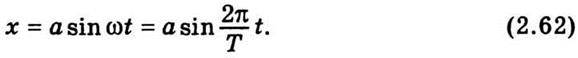
Розглядаючи зміну проекції точки В на горизонтальну вісь, аналогічно дістанемо
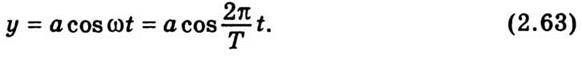
Коливальний характер руху, вираженого рівняннями (2.62) і (2.63), стає особливо наочним, якщо подати їх графічно, як це зроблено на рис. 2.11. Коливальний рух, що описується функцією синуса або косинуса, називається простим гармонічним коливанням. Цей рух повністю визначається такими величинами: 1. Амплітудою а – відстанню найбільшого відхилення від початкового положення. 2. Періодом коливань Т, тобто часом, протягом якого точка (тіло), що коливається, здійснить повний цикл коливального руху, зміщуючись спочатку в один, а потім у другий бік від початкового положення і знову повертаючись до нього. Замість періоду коливань можна задати його частоту ν, що визначається кількістю повних коливань за 1 с. За одиницю частоти взято 1 герц (Гц) – це частота такого коливання, період якого дорівнює 1 с. Період і частота зв’язані між собою так:

Колова частота ω дорівнює кількості повних коливань за 2π секунд:

Визначимо силу, під дією якої виникатимуть прості гармонічні коливання. Для цього скористаємось, наприклад, рівнянням (2.62) і знайдемо спочатку швидкість υ і прискорення W для точки, що гармонічно коливається:
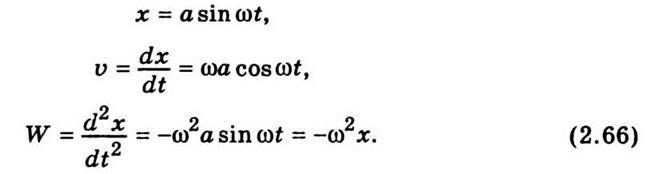
Помноживши ліву й праву частини рівняння (2.66) на масу матеріальної точки, дістанемо диференціальне рівняння простого гармонічного коливання:

Де с = mω2 – коефіцієнт зворотної сили. Отже, тіло здійснюватиме просте гармонічне коливання, якщо на нього діятиме зворотна сила, пропорційна зміщенню тіла від положення рівноваги. Гармонічне коливання – це рух, спричинений силою, що змінюється пропорційно відхиленню х тіла від положення рівноваги. Сила F = – сх повністю характеризує коливання тіла поблизу положення рівноваги, тобто при малих амплітудах коливання. Зі збільшенням амплітуди коливань може настати ангармонічність і пропорційність між зворотною силою і зміщенням тіла порушується.
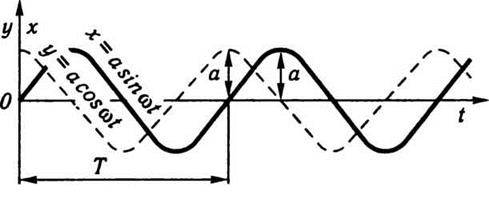
Рис. 2.11