Мішані числа
Розділ 2 ДРОБОВІ ЧИСЛА І Дії З НИМИ
§ 31. Мішані числа
На координатному промені (рис.243) зображено неправильний дріб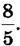 
Він містить 1 цілу одиницю та ще 
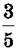одиниці. Це записують так:
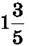(читається: “одна ціла три п’ятих”). Число 
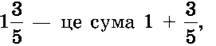яка записана без знака додавання. Число 1 називають цілою частиною числа 
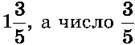– його дробовою частиною. Розглянуті числа 
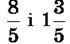рівні між собою: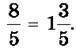 
Кажуть,
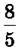виділено цілу та дробову частини.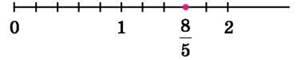
Рис. 243
Щоб виділити цілу та дробову частини з неправильного дробу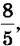 
розділимо 8 на 5. Маємо непо вну частку 1 і остачу 3. Число 1 дає цілу частину, а остача 3 – чисельник дробової частини.
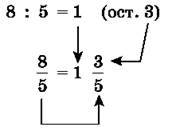
Щоб виділити цілу частину з неправильного дробу, треба поділити чисельник неправильного дробу на знаменник. Тоді неповна частка буде цілою частиною, остача – чисельником дробової частини, а знаменник неправильного дробу – знаменником дробової
Приклад 1. З неправильного дробу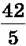 
виділи цілу та дробову частини.
Розв’язання. Ділимо 42 на 5. Маємо неповну частку 8 і остачу 2. Отже,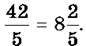 
Такі числа, як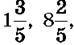 
називають мішаними числами (або мішаними дробами).
Якщо чисельник неправильного дробу ділиться без остачі на знаменник, то цей дріб буде натуральним числом – часткою від ділення чисельника назнаменник. Наприклад,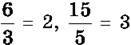 
тощо. Кажуть, що числа 
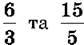не мають дробової частини (або дробова частина дорівнює нулю). Правильні дроби 
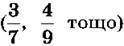не мають цілої частини. Кажуть, що ціла частина правильного дробу дорівнює нулю.
Початковий рівень
1031. Прочитай числа:
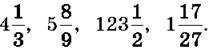Назви цілу та дробову частини чисел. 1032. Запиши коротше:
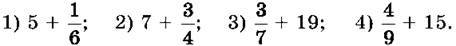
1033. Запиши коротше:
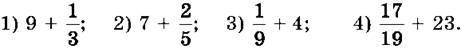
1034. Запиши число у вигляді суми його цілої і дробової частин:
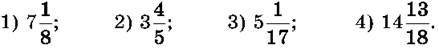
1035. Запиши число у вигляді суми його цілої і дробової частин:
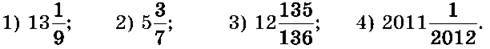
1036. Наведи приклад чисел, у яких ціла частина дорівнює нулю. Як називаються такі числа?
1037. Наведи приклад чисел, у яких дробова частина дорівнює нулю. Як називаються такі числа?
Середній рівень
1038. Виділи цілу і дробову частини числа:
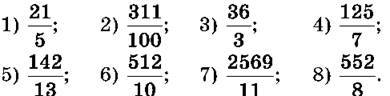
1039. Виділи цілу і дробову частини числа:
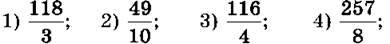
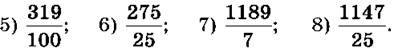
1040. Запиши частку у вигляді дробу і перетвори на мішане число:
1) 10 : 3; 2) 113 : 7; 3) 125 : 10; 4) 139 : 15.
1041. Запиши частку у вигляді дробу і перетвори на мішане число:
1) 27 : 2; 2) 147 : 5; 3) 313 : 13; 4) 3189 : 1000.
Достатній рівень
1042. Порівняй:
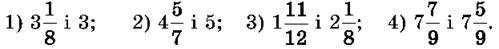
1043. Порівняй:
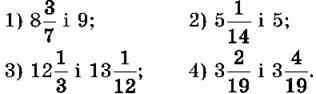
1044. Накресли координатний промінь, взявши за одиничний відрізок 5 клітинок. Познач на ньому точки, що відповідають неправильним дробам
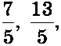
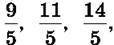попередньо виділивши цілу та дробову частини кожного з них.
1045. Вирази:
1) у кілометрах: 8 км 113 м, 3 км 8 м;
2) у годинах: 3 год 19 хв, 7 год 1 хв.
1046. Порівняй:
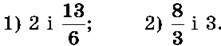
1047. Порівняй:
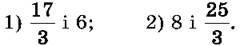
1048. Порівняй дроби, записавши їх у вигляді мішаних чисел:
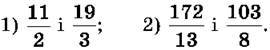
1049. Виділи цілу й дробову частини і запиши всі числа в порядку їх зростання:
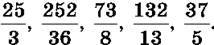
Високий рівень
1050. Які натуральні числа можна підставити замість n, щоб нерівність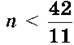 
була правильною?
1051. Яке найменше натуральне число можна підставити замість m, щоб нерівність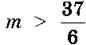 
була правильною?
1052. Яким найбільшим натуральним числом можна замінити m, щоб нерівність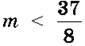 
була правильною?
1053. Запиши три числа, що більші за 7, але менші від 8.
1054. Турист пройшов 19 км за 4 год. Знайди його швидкість.
1055. Учень розв’язав 9 рівнянь за 32 хв. Скільки хвилин у середньому він розв’язував одне рівняння?
1056. На пошиття 15 однакових костюмів майстерня пані Шапокляк витратила 32 м тканини. Чи вистачить 2 м тканини на пошиття одного костюма?
1057. Мавпочка Абу розфасувала 41 кг бананів у 5 однакових ящиків. Чи можна помістити в один ящик 8 кг бананів?
1058. Перша бригада з площі 80 м2 зібрала 6 ц моркви, друга з 90 м2 – 6 ц 20 кг, а третя зі 100 м2 – 8 ц. На ділянці якої з бригад (у кг з 1 м2) урожайність була найбільшою? У якої – найменшою?
1059. Підбери три таких натуральних числа а, при яких виконується подвійна нерівність:
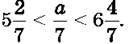
Вправи для повторення
1060. Напиши:
1) найбільший правильний дріб зі знаменником 17;
2) найменший неправильний дріб із чисельником 20.
1061. Які цифри можна підставити замість зірочок, щоб:
(1 votes, average: 5.00 out of 5)
Loading...