Головна ⇒ 📌Математика ⇒ МНОЖЕННЯ І ДІЛЕННЯ БАГАТОЦИФРОВИХ ЧИСЕЛ НА ОДНОЦИФРОВЕ ЧИСЛО

МНОЖЕННЯ І ДІЛЕННЯ БАГАТОЦИФРОВИХ ЧИСЕЛ НА ОДНОЦИФРОВЕ ЧИСЛО

531. Прочитай про дію множення та її закони.

Помножити натуральне число 3 на натуральне число 5 – означає знайти суму п’яти доданків, кожен з яких дорівнює

3 : 3 ∙ 5 = 3 + 3 + 3 + 3 + 3.

Числа 3 і 5 називають множниками, а вираз 3 ∙ 5 – їх добутком.

Пам’ятай: а ∙ 1 = а, а ∙ 0 = 0.

Переставний закон множення. Для будь-яких натуральних чисел а і b виконується рівність а ∙ b = b ∙ а, яка виражає переставний закон множення.

Від перестановки множників добуток не змінюється.

Сполучний

закон множення. Для будь-яких натуральних чисел виконується рівність (а ∙ b) ∙ с = а ∙ (b ∙ с), яка виражає сполучний закон множення.

Щоб добуток двох чисел помножити на третє число, можна перше число помножити на добуток другого і третього чисел.

Наприклад: (3 ∙ 5) ∙ 2 = 3 ∙ (5 ∙ 2). У лівій і правій частинах рівності маємо той самий добуток 30.

З переставного та сполучного законів множення дістаємо ще одну властивість.

У добутку кількох множників можна переставляти множники і брати їх у дужки будь-яким чином.

Наприклад: 3 ∙ 4 ∙ 25 ∙ 30 = (3 ∙ 30) ∙ (4 ∙ 25).

532. Знайди добуток зручним способом.

8 ∙

4 ∙ 50 2 ∙ 4 ∙ 5 ∙ 15 4 ∙ 6 ∙ 25

533. Прочитай про наступний закон множення.

Розподільний закон множення. Для будь-яких натуральних чисел а, b і с істинна рівність (а + b) ∙ с = а ∙ с + b ∙ с, що виражає розподільний закон множення.

Добуток суми двох чисел на будь-яке число дорівнює сумі добутків кожного доданка на це число.

Розподільний закон виконується для будь-якого числа доданків.

Наприклад: (1 + 2 + 3 + 4 + 5 + 6) ∙ 7 = 1 ∙ 7 + 2 ∙ 7 + 3 ∙ 7 + 4 ∙ 7 + 5 ∙ 7 + 6 ∙ 7.

Застосовуючи розподільний закон множення, суму і число можна міняти місцями.

4 ∙ (5 + 8) = (5 + 8) ∙ 4 = 5 ∙ 4 + 8 ∙ 4

534. Які із задач розв’язуються дією множення?

1) У класі 15 парт. Скільки парт у 5 таких класах?

2) Перше число 8, а друге – на 4 більше. Знайди друге число.

3) Перше число 8, а друге – у 4 рази більше. Знайди друге число.

4) Вміст крохмалю в картоплі становить її маси.

Скільки кілограмів картоплі потрібно взяти, щоб одержати 200 кг крохмалю?

535. Який добуток більший і на скільки?

245 ∙ 45 чи 245 ∙ 46 468 ∙ 25 чи 468 ∙ 24

536.

207 ∙ 4 36 ∙ 23 1 ∙ 0 + 4 ∙ 1 200 : 100

288 : 8 928 : 32 8 : 1 + 6 : 6 230 : 10

537. За даними таблиці склади та розв’яжи задачу.

Рухомий об’єкт

Швидкість

Час

Відстань

Велосипедист

Вершник

15 км/год

12 км/год

Однаковий

30 км

538. Відстань між двома містами 72 км. Третину цієї відстані поїзд пройшов за 12 хв. З якою швидкістю йшов поїзд? (Розв’яжи задачу складанням виразу.)

539°.

203 ∙ 4 49 ∙ 18 14 т 7 ц – 5 т 9 ц

23 ∙ 4 792 : 24 12 т 70 кг – 9 т 500 кг

540°. У першій школі а учнів, у другій – на b учнів менше, ніж у першій. У третій школі на 119 учнів менше, ніж у другій. Скільки учнів у третій школі? Склади вираз та обчисли його, якщо а = 1758, b = 95.

541. Поясни усний і письмовий способи обчислень.

263 ∙ 3 = (200 + 60 + 3) ∙ 3 = 200 ∙ 3 + 60 ∙ 3 + 3 ∙ 3 = 600 + 180 + 9 = 789

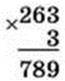
542. Письмове множення багатоцифрових чисел на одноцифрове число виконують так само, як і трицифрових. Розглянь обчислення виразу 201 852 ∙ 4 і прочитай пояснення.

Пояснення. Підписуємо число 4 під одиницями першого множника. Помножимо 2 од. на 4, буде 8 од., підписуємо їх під одиницями. Помножимо 5 дес. на 4, буде 20 дес., або 2 сот. У розряді десятків у добутку пишемо 0, а 2 сот. запам’ятовуємо. 8 сот. помножити на 4, буде 32 сот., та ще 2 сот., буде 34 сот., або 3 тис. і 4 сот. 4 сот. записуємо під сотнями, а 3 тис. запам’ятовуємо. 1 тис. помножити на 4, буде 4, та ще 3 тис., буде 7 тис. Записуємо 7 тис. під тисячами. 0 дес. тисяч помножити на 4, буде 0 дес. тисяч. Запишемо число 0 під дес. тис. 2 сот. тис. помножити на 4, буде 8 сот. тис. Запишемо 8 під сот. тис. Добуток 807 408.

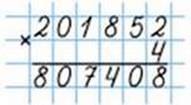
543. Перевір, чи є серед чисел 351 462, 57 876, 362 278, 2304, 8347 значення поданих виразів.

384 ∙ 6 51 754 ∙ 7 117 154 ∙ З

544. Обчисли з поясненням: 25 454 ∙ 5.

545. Знайди помилки в обчисленнях.

546. На будівництво підвозили цеглу автомобілем і трактором з причепом. На автомобіль щоразу навантажували 925 цеглин, а на причіп – 2075. За день автомобіль зробив 6 рейсів, а трактор – 3. Скільки всього цеглин завезли на будівництво протягом дня?

547*. Скільки потрібно цифр, щоб пронумерувати 150 сторінок книжки?

548°. Для покриття черепицею даху великого будинку потрібно 2146 плиток, а малого – 1428. Скільки потрібно плиток, щоб покрити черепицею дахи 6 таких великих і 7 малих будинків?

549°. 2306 ∙ 6 17 245 ∙ 8 35 511 ∙ 7 684 : 4

550. (Усно.)

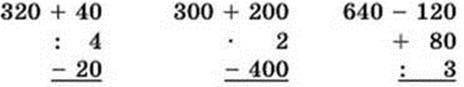
551. Закінчи обчислення.

552. 2306 ∙ 6 30 094 ∙ 7 40 801 ∙ 9 40 059 ∙ З

553. Парні числа збільш у 6 разів, а непарні – зменш на 6: 20 756, 3015, 4006, 17 201.

554. У великому залі кінотеатру 1224 місця, а в малому – 208 місць. Скільки кіноглядачів може обслугувати кінотеатр за день, якщо у великому залі було k сеансів, а в малому – с? Склади вираз для розв’язування задачі та знайди його значення, якщо k = 5 і с = 4.

555. Від однієї пристані одночасно в одному напрямку вирушили катер і буксир. Швидкість катера 27 км/год, а буксира – 18 км/год. Яка відстань буде між ними через 3 год? (Розв’яжи задачу двома способами.)

556. У цистерні було 3400 л бензину. Наповнили 4 однакові бочки, і в цистерні залишилося 2600 л бензину. Скільки літрів бензину налили в кожну бочку?

557. 40 037 ∙ 2 34 050 ∙ 4 80 015 ∙ 4 744 : 24

558. 1) Скільки всього в кожному числі сотень; тисяч: 3400, 7000, 2404, 140 000?

2) Запиши кожне число за допомогою цифр.

5 сот. 240 сот. 3 дес. 180 дес. 5 тис.

559. Поясни, як міркували, знаходячи добутки.

560. 1) Розглянь, як можна записувати дію множення, якщо один з множників має нулі в кінці.

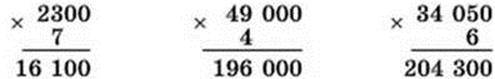
2) 6700 ∙ 2 84 000 ∙ 6 130 000 ∙ 7 760 ∙ 5

561. Знайди значення виразу а ∙ 10 + 300 для таких значень змінної а: 4, 40, 400, 210.

562*. Три дівчинки Мальва, Маргарита і Лілія тримали в руках квіти: мальви, маргаритки та лілії. Жодна з них не тримала квіти, від назви яких походить її ім’я. Маргарита уважно розглядала лілії, які тримала подруга. Хто які квіти тримав?

563. Один оператор набирає за день на комп’ютері 20 сторінок тексту, а другий – 24 сторінки. Скільки сторінок вони наберуть за k днів, якщо працюватимуть разом? Склади вираз для розв’язування задачі та знайди його значення, якщо k = 5.

564. Розглянь числові дані на малюнках і знайди відповіді на запитання.

1) Яка маса 6 таких коней? 2 корів? 10 овець?

2) На скільки маса 2 корів більша від маси коня?

3) Маса скількох кіз дорівнює масі однієї корови?

4) Чому дорівнює маса 5 таких кіз і 4 овець разом?

565°.

2300 ∙ 5 14 ц 9 кг – 6 ц 28 кг 2 кг – 300 г

2140 ∙ 5 4 м 75 см + 9 м 9 см 2 ц : 5

566°. Маса курки 2 кг 375 г, а маса гуски на 2 кг 345 г більша, ніж маса курки. Маса індика на 2 кг 350 г більша, ніж маса гуски й курки разом. Яка загальна маса курки, гуски та індика?

567. 1) (Усно.)

20 ∙ 4 3 ∙ 14 20 ∙ 10 ∙ 2 1200 ∙ 5

25 ∙ 2 2 ∙ 41 2 ∙ (3 + 30) 101 ∙ 7

2) Виконай множення, переставивши множники.

4 ∙ 978 6 ∙ 5738 8 ∙ 50 400

568. Прочитай задачу і розглянь її розв’язання.

Задача. У кондитерський цех хлібокомбінату привезли 2756 ящиків масла по 7 кг. Скільки всього кілограмів масла привезли?

Розв’язання: 7 ∙ 2754 = 19 292 (кг).

Відповідь: усього привезли 19 292 кг масла.

569. 1) 4 ∙ 20 374 7 ∙ 35 705 3 ∙ 123 401 2 ∙ 240 756

2) Перевір правильність обчислення виразу.

4 ∙ 65 701 – 867 : 3 = 262 515

570. 4078 ∙ 8 + 25 409 6 ∙ 43 051 – 28 ∙ 35

571. Автобус проїхав а км за b год. Яку відстань із такою самою швидкістю він проїде за 3 год? Склади вираз для розв’язування задачі.

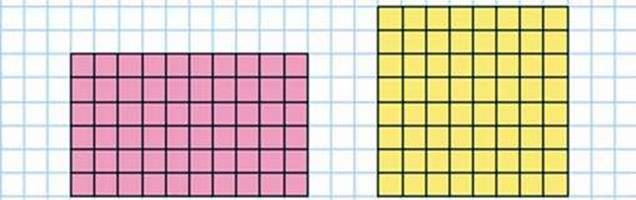
572. Полічи двома способами кількість клітинок у кожному прямокутнику. У якому прямокутнику клітинок більше? Порівняй периметри прямокутників.

573. Перший насос може викачати 24 т води за 6 год, а другий – за 3 год. За скільки годин викачають цю воду обидва насоси, працюючи одночасно? Розглянь план розв’язування. Розв’язання запиши.

План розв’язування:

1) Скільки тонн води викачає перший насос за 1 год?

2) Скільки тонн води викачає другий насос за 1 год?

3) Скільки тонн води викачають насоси за 1 год?

4) За скільки годин вони обидва викачають 24 т води?

574°.

9 ∙ 75 046 3 ∙ 348 + 407 ∙ 7 2 кг – 200 г

200 275 ∙ 4 5 ∙ 280 – 280 : 10 2 м – 200 см

575°. Побудуй прямокутник ABCD зі сторонами 2 см 5 мм і 4 см 5 мм. Знайди периметр прямокутника.