Множення многочлена на многочлен
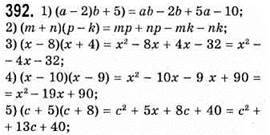
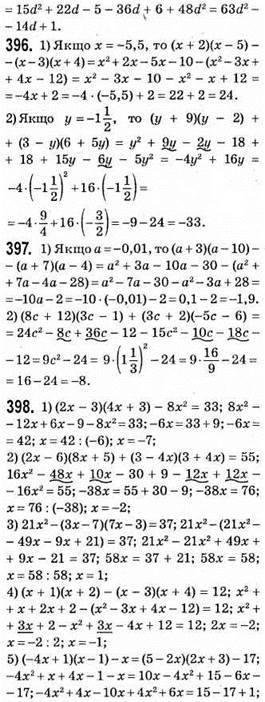
0x = -1: рівняння коренів не має.
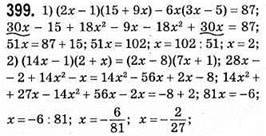
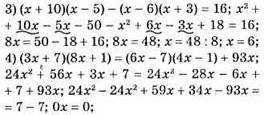
Коренем рівняння є будь-яке число.
Отже, значення виразу не залежить від змінної.
404. (х – 3)(х2 + 7) – (х – 2)(х2 – х + 5) = х3 – 3х2 + 7х – 21 – (х3 – х2 + 5х – 2х2 + 2х – 10) = х3 – 3х2 + 7х – 21 – х3 + х2 – 5х + 2х2 – 2х + 10 = -11. Отже, значення виразу дорівнює -11 при будь-яких значеннях х.
405. Нехай х; х + 1; х + 6; х + 8 – шукані числа.
Тоді
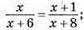х2 + 8х = х2 + 6х + х + 6; 8х – 7х = 6; х = 6.6; 7; 12; 14 – шукані числа.
406. Нехай х; х + 4; х + 10 – шукані числа.
Тоді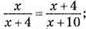 
х2 + 10х = х2 + 4х + 4x + 16; 10x – 8x = 16; 2х = 16; x = 8.
8; 12; 18 – шукані числа.
407. Нехай х; х + 1; х + 2; х + 3 – послідовні натуральні числа, тоді (х + 1) • (х + 3) – 17 = х(х + 2); х2 + х + 3х + 3 – 17 = х2 + 2х; х2 – х2 + 4х – 2х = 14; 2х = 14; x = 7.
7; 8; 9; 10 – шукані числа.
408. Нехай х; х + 1; х + 2 – шукані числа. Тоді (х + 1)(х + 2) – 50 = х2; х2 + х + 2х + 2 – х2 = 50; 3х = 50 – 2; 3х = 48; х = 48 : 3; х = 16.
16; 17; 18 – шукані числа.
409. Нехай сторона квадрата х см, тоді сторони прямокутника (х + 3)
410. Нехай х см – одна сторона прямокутника, тоді (30 – х) см – друга сторона прямокутника. Якщо одну сторону зменшити на 5 см, то вона буде рівна (х – 5) см, а якщо другу збільшити на 3см, то вона буде рівна (30 – х + 3) = (33 – х) см. Площа зменшиться на 21 см2, тому х • (30 – х) – (х – 5)(33 – х) = 21; 30х – х2 – (33х – 165 – х2 + 5х) = 21; 30х – х2 – 33х + 165 + х2 – 5х = 21; -8х = -165 + 21; -8х = -144; х = -144 : (-8); х = 18 (см) – одна сторона прямокутника.
30 – 18 = 12 см – друга сторона прямокутника.
411. Нехай ширина прямокутника x см, тоді довжина його (x + 2) см, а площа х(х + 2) см2. Якщо довжину збільшити на 2 см, а ширину зменшити на 4 см, то виміри будуть рівні (х – 4) см і (х +4) см, а площа прямокутника (x – 4) • (x + 4) см2.
За умовою x(x + 2) – (x + 4)(x – 4) = 40; x2 + 2x – (x2 + 4x – 4x – 16) = 40; x2 + 2x – x2 + 16 = 40; 2x = 40 – 16; 2x = 24; x = 12 см – ширина прямокутника.
12 + 2 = 14 см – довжина прямокутника.
412. 1) x2 – 8x + 7 = (x – 1)(x – 7) – тотожність; x2 – 8x + 7 = x2 – x – 7x + 7; x2 – 8x + 7 = x2 – 8x + 7 – правильна рівність;
2) у2(y – 7)(y + 2) = y4 – 5y3 – 14y2 – тотожність; у2(у2 – 7y + 2y – 14) = y4 – 5y3 – 14y2; у4 – 5у3 – 14y2 = y4 – 5y3 – 14y2 – правильна рівність;
3) а3 – 8 = (а – 2)(а2 + 2а + 4) – тотожність; а3 – 8 = а3 + 2а2 + 4а – 2а2 – 4а – 8; а3 – 8 = а3 – 8 – правильна рівність;
4) (а – 1)(а + 1)(а2 + 1) = а4 – 1 – тотожність; (а2 – а + а – 1)(а2 + 1) = а4 -1; (а2 -1) • (а2 + 1) = а4 – 1; а4 – а2 + а2 – 1 = а4 – 1; а4 – 1 = а4 – 1 – правильна рівність;
5) (а4 – а2 + 1)(а4 + а2 + 1) = а8 + а4 + 1 – тотожність; a8 – а5 + а4 + а6 – а4 + а2 + а4 – а2 + 1 = а8 + а4 + 1; а8 + а4 + 1 = а8 + а4 + 1 – правильна рівність.
413. 1) 3a2 + 10a + 3 = 3(a + 3)(a + 1/3) – тотожність;
3а2 + 10а + 3 = (3а + 9)(а + 1/3); 3а2 + 10а + 3 = 3а2 + 9а + а + 3; 3а2+ 10а + 3 = 3а2 + 10а + 3 – правильна рівність при будь-яких значеннях а;
2) (а + 1)(а2 + 5а + 6) = (а2 + 3а + 2) • (а + 3) – тотожність;
А3 + а2 + 5а2 + 5а + 6а + 6 = а3 + 3а2 + 2а + 3а2 + 9а + 6; а3 + 6а2 + 11а + 6 = а3 + 6а2 + 11а + 6 – правильна рівність при будь-яких значеннях а;
3) (а + 1)(а4 – а3 + а2 – а + 1) = а5 + 1 – тотожність;
А5 – а4 + а3 – а2 + а + а4 – а3 + а2 – а + 1 = а5 + 1; а5 + 1 = а5 + 1 – правильна рівність при будь-яких значеннях а.
414. (n + 9)(n + 11) – (n + 3)(n + 5) = n2 + 9n + 11n + 99 – n2 – 3n – 5n – 15 = 12n + 84 = 12(n + 7) – кратне 12 при будь-яких значеннях n, бо 12 кратне 12.
415. (n + 29)(n + 3) – (n + 7)(n + 1) = n2 + 29n + 3n + 87 – n2 – 7n – n – 7 = 24n + 80 = 8(3n + 10) – кратне 8 при всіх значеннях n.
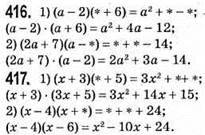
418. Нехай х; х + 1; х + 2; х + 3 – шукані числа.
(х + 1)(х + 2) – х(х + 3) = х2 + 2х + х + 2 – х2 – 3х = 2. Ця різниця не залежить від вибору числа, вона завжди дорівнює 2.
419. Нехай х; х + 1; х + 2 – шукані числа.
(х + 1)2 – х(х + 2) = (х + 1)(х + 1) – х2 – 2х = х2 + х + х + 1 – х2 – 2х = 1. Ця різниця дорівнює 1 і не залежить від вибору числа.
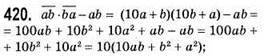
Ділиться націло на 10 незалежно від значень а і b.
421. х = 6n + 3; у = 6n + 2; ху = (6n + 3) • (6n + 2) = 36n2 + 18n + 12n + 6 = 6(6n2 + 5n + 1); ділиться націло на 6.
422. a = 8n + 3; b = 8n + 7; а • b = (8n + 3) • (8n + 7) = 64n2 + 24n + 56n + 21 = 64n2 + 80n + 21 = 64n2 + 80n + 16 + 5 = 8(8n2 + 10n + 2) + 5. Отже, остача від ділення ab на 8 дорівнює 5.
423. m = 11а = 9; n = 11b + 5; m • n = (11а + 9)(11b + 5) = 121аb + 99b + 55а + 45 = 121аb + 99b + 55а + 44 + 1 = 11(11аb + 9b + 5а + 4) + 1. Отже, при діленні mn на 11 остача дорівнює 1.
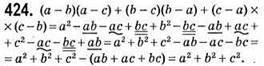
425. Нехай І робітник за 1 год виготовляє х деталей, тоді II виготовляє (26 – х) деталей. І робітник за 5 год виготовить 5х деталей, а II за 3 год виготовить 3(26 – х) деталей. Разом вони виготовили 108 деталей.
Отже, 5х + 3(26 – х) = 108; 5х + 78 – 3х = 108; 2х = 108 – 78; 2х = 30; х = 30 : 2; x = 15 деталей виготовляє за 1 годину І робітник.
26 – 15 = 11 деталей виготовляє за 1 годину II робітник.
426. 1) 0,05 • 72 = 3,6 г солі у І розчині;
2) 0,15 • 48 = 7,2 г солі у II розчині;
3) 3,6 + 7,2 = 10,8 г солі у розчині;
4) 72 + 48 = 120 г маса розчину;
5) 
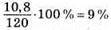вміст солі у розчині.
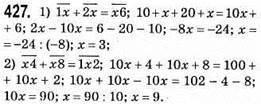
428. 1) 1816n = 128n • 912n – тотожність;
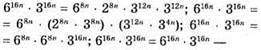
Правильна рівність;
2) 758n = 2254n • 6252n – тотожність; 758n = 254n • 94n • 254n; 758n = 258n • 38n; 758n = 758n – правильна рівність.
429. Нехай Демохар прожив х років, тоді 1/4х – життя хлопчиком; 1/5х – життя юнаком; 1/3х – життя зрілою людиною. а
Тоді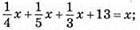 
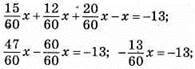
Х = 60 років прожив Демохар.
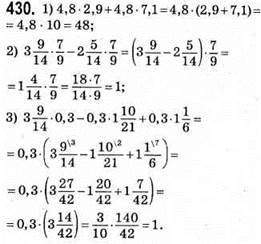
431. 1) x(x + 4) = 0; x = 0 або x + 4 = 0; х = -4;
2) (х – 6)(х + 9) = 0; х – 6 = 0, х = 6 або х + 9 = 0, х = -9;
3) (3х + 5)(10 – 0,4х) = 0;
3х + 5 = 0; 3х = -5; х = -5/3;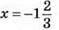 
або 10 – 0,4х = 0; -0,4х = -10; х = -10 : (-0,4); х = 25.
(1 votes, average: 5.00 out of 5)
Loading...