Головна ⇒ 📌Довідник з математики ⇒ Модуль числа
Модуль числа
Математика – Алгебра
Раціональні числа
Модуль числа
Відстань від початку відліку до точки, що зображає число на координатній прямій, називається Модулем даного числа. Позначення: 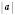 – модуль а. Очевидно, що для додатних чисел і 0
– модуль а. Очевидно, що для додатних чисел і 0 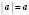 , для від’ємних
, для від’ємних 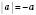 .
.
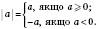
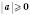 для будь-якого числа а.
для будь-якого числа а.
Модулі протилежних чисел рівні: 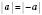 .
.
Приклади
1) 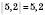 ;
; 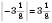 ;
; 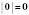 .
.
2) Розв’яжіть рівняння.
а) 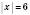 ;
; 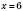 або
або 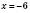 .
.
б) 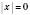 ;
; 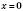 .
.
в) 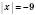 ; рівняння не має коренів, тому що модуль числа не може бути від’ємним.
; рівняння не має коренів, тому що модуль числа не може бути від’ємним.
Related posts:
- Модуль раціонального числа Урок № 6 6 Тема. Модуль раціонального числа Мета: сформувати уявлення учнів про геометричний зміст поняття “модуль числа”; виробити вміння читати, записувати вирази, що містять модуль, а також знаходити значення виразів, що містять числа під знаком модуля. Тип уроку: засвоєння нових знань і вмінь Хід уроку І. Перевірка домашнього завдання Усні вправи 1. Обчисліть А) […]...
- МОДУЛЬ ЧИСЛА Розділ 4 РАЦІОНАЛЬНІ ЧИСЛА ТА ДІЇ З НИМИ § 23. МОДУЛЬ ЧИСЛА Позначимо на координатній прямій точки А (-6), В (-2) і С (2) (мал. 104). Яка точка розміщена найдалі від початку відліку О? Точка А, оскільки ОА = б од., а ОВ = ОС = 2 од. Мал. 104 Порівнюючи відстані від точок А, […]...
- Застосування модуля числа. Відстань між точками на координатній прямій Урок № 6 7 Тема. Застосування модуля числа. Відстань між точками на координатній прямій Мета: поглибити знання учнів про властивості модуля раціонального числа та відпрацювати навички застосування означення та властивостей модуля для розв’язування рівнянь та нерівностей. Тип уроку: застосування знань, умінь і навичок Хід уроку I. Перевірка домашнього завдання Математичний диктант Варіант 1 [2] 1. […]...
- Властивості модуля – Модуль і його властивості Математика – Алгебра Модуль і його властивості Модуль числа – це відстань від 0 до точки, що відповідає цьому числу на координатній прямій, виміряна в одиничних відрізках. Отже, для всіх значень a. Властивості модуля 1. . 2. Якщо , то . 3. Якщо , то 4. Модуль суми скінченного числа дійсних чисел не перевищує суми […]...
- Подільність цілих чисел Формули й таблиці МАТЕМАТИКА Подільність цілих чисел Ціле число а ділить ціле число b, або b ділиться на а, якщо існує таке ціле число с, при якому b = ас. Це має місце тоді, коли остача від ділення числа b на число а дорівнює нулю. Подільність цілих чисел має такі властивості: 1. Будь-яке ціле число […]...
- Раціональні числа, ірраціональні числа, дійсні числа, числові множини, етапи розвитку числа Урок № 37 Тема. Раціональні числа, ірраціональні числа, дійсні числа, числові множини, етапи розвитку числа Мета: систематизувати, узагальнити знання учнів щодо поняття числа та видів чисел, сформувати уявлення про множину дійсних чисел; сформувати вміння учнів відтворювати означення та властивості видів чисел, вивчених на уроці, виконувати найпростіші дії з дійсними числами (зокрема порівняння), використовувати вивчені властивості […]...
- Ділення раціональних чисел Математика – Алгебра Раціональні числа Ділення раціональних чисел Часткою двох від’ємних чисел є число додатне. Щоб знайти його модуль, треба модуль діленого поділити на модуль дільника. Часткою двох чисел із різними знаками є число від’ємне. Щоб знайти його модуль, треба модуль діленого поділити на модуль дільника. Для будь-якого числа а: ; ; Для : ; […]...
- Протилежні числа. Цілі числа. Раціональні числа Розділ 4 Раціональні числа і дії мідними §35. Протилежні числа. Цілі числа. Раціональні числа Точки A і B з відповідними координатами 2 і -2 однаково віддалені від початку відліку – точки О і знаходять ся по різні боки від неї (мал. 71). Щоб потрапити з точки О в точки A(2) і B(-2), треба відкласти однакові […]...
- Додавання раціональних чисел Математика – Алгебра Раціональні числа Додавання раціональних чисел Щоб додати два від’ємних числа, треба додати їхні модулі й поставити перед одержаним числом знак “–”: . Щоб додати два числа з різними знаками, треба від більшого модуля відняти менший і поставити перед одержаним числом знак того доданка, модуль якого більший: ; . Сума двох протилежних чисел […]...
- Раціональні числа; порівняння, додавання та віднімання. Розв’язування вправ Урок № 7 8 Тема. Раціональні числа; порівняння, додавання Та віднімання. Розв’язування вправ Мета: підготувати учнів до виконання тематичної контрольної роботи. Тип уроку: узагальнення та систематизація знань, умінь і навичок. Хід уроку I. Перевірка домашнього завдання @ Якщо на попередньому уроці не встигли зробити, то на початку цього уроку ми проводимо тестову роботу (з теми […]...
- Дійсні числа Математика – Алгебра Квадратні корені Раціональні числа – це числа, які можуть бути записані у вигляді , де m – ціле число, n – натуральне. Кожне раціональне число можна подати у вигляді нескінченного періодичного десяткового дробу. І навпаки, кожний нескінченний періодичний десятковий дріб є раціональним числом. Числа, які зображуються нескінченними неперіодичними десятковими дробами, називають ірраціональними. […]...
- Тригонометричний запис комплексного числа – КОМПЛЕКСНІ ЧИСЛА Формули й таблиці МАТЕМАТИКА КОМПЛЕКСНІ ЧИСЛА Тригонометричний запис комплексного числа Z = r (cosα + isinα) R = – модуль комплексного числа; α – аргумент комплексного числа; Значення α, узяте в межах одного кола, -π < α < π називається головним значенням аргументу....
- ЧИСЛА І ЦИФРИ. ОДНОЦИФРОВІ ЧИСЛА. СКЛАДАННЯ ПРИКЛАДІВ ЗА ЧИСЛОВИМИ ПРОМЕНЯМИ. ПОРІВНЯННЯ ЧИСЕЛ ОЗНАКИ І ВЛАСТИВОСТІ ПРЕДМЕТІВ. МНОЖИНИ. ГЕОМЕТРИЧНІ ФІГУРИ. НАТУРАЛЬНІ ЧИСЛА 1-10 І ЧИСЛО 0 Урок 34. ЧИСЛА І ЦИФРИ. ОДНОЦИФРОВІ ЧИСЛА. СКЛАДАННЯ ПРИКЛАДІВ ЗА ЧИСЛОВИМИ ПРОМЕНЯМИ. ПОРІВНЯННЯ ЧИСЕЛ Мета: ознайомити учнів з поняттям “одноцифрові числа”; узагальнити поняття “число” і “цифра”; учити порівнювати числа, складати приклади за числовими променями; розвивати мислення; виховувати інтерес до математики. Хід уроку […]...
- Прості й складені числа Математика – Алгебра Подільність натуральних чисел Прості й складені числа Натуральне число називається Простим, якщо воно має тільки два різних дільники: одиницю й саме це число. Число, яке має більше двох дільників, називається складеним. Число 1 має єдиний дільник – 1, тому не належить ні до простих, ні до складених чисел. Приклади 1) Числа 2, […]...
- Лінійні рівняння з одним невідомим Математика – Алгебра Рівняння Лінійні рівняння з одним невідомим Рівняння виду , де a і b – деякі числа, а х – невідоме, називається Лінійним рівнянням з одним невідомим. Числа a і b називають Коефіцієнтами. Кількість коренів лінійного рівняння 1. Якщо , лінійне рівняння має єдиний корінь: . 2. Якщо , , лінійне рівняння коренів […]...
- Дільники натурального числа. Прості і складені числа Урок № 1 Тема. Дільники Натурального Числа. Прості І Складені Числа Мета: систематизувати знання учнів про зміст дії ділення натуральних чисел; розширити знання учнів про властивості ділення натуральних чисел, доповнити їх уявленням про такі поняття, як дільник числа, кратне числу, прості і складені числа; сформувати вміння учнів знаходити дільник числа та класифікувати натуральні числа залежно […]...
- ЦІЛІ ЧИСЛА. РАЦІОНАЛЬНІ ЧИСЛА Розділ 4 РАЦІОНАЛЬНІ ЧИСЛА ТА ДІЇ З НИМИ § 24. ЦІЛІ ЧИСЛА. РАЦІОНАЛЬНІ ЧИСЛА У п’ятому класі ви вивчали натуральні числа. Це числа, які використовують для лічби: 1; 2; 3; 4; … . Усі натуральні числа утворюють множину натуральних чисел. Цю множину позначають буквою N. Множина N має нескінченно багато елементів, оскільки натуральних чисел нескінченно […]...
- Раціональні числа: додавання і віднімання. Розв’язування вправ Урок № 79 Тема. Раціональні числа: додавання і віднімання. Розв’язування вправ Мета: підготувати учнів до виконати тематичної контрольної роботи. Тип уроку: узагальнення та систематизації знань, вдосконалення вмінь. Хід уроку І. Перевірка домашнього завдання @ Оскільки вправи домашнього завдання дублюють вправи, розв’язані на попередньому уроці, доцільно з метою збереження часу, перевірити вибірково зошити у “слабких” учнів […]...
- Протилежні числа Урок № 6 4 Тема. Протилежні числа Мета: сформувати уявлення про зміст поняття “протилежні числа”; навчити знаходити й записувати число, протилежне до даного, розв’язувати рівняння, що передбачають застосування поняття числа, протилежного до даного. Тип уроку: засвоєння вмінь та навичок. Хід уроку І. Перевірка домашнього завдання Математичний диктант Варіант 1 [2] 1. Запишіть число “мінус три” […]...
- Порівняння чисел Математика – Алгебра Раціональні числа Порівняння чисел Із двох чисел меншим є те, зображення якого на горизонтальній координатній прямій розташовано ліворуч, більшим – те, зображення якого розташовано праворуч. Будь-яке додатне число більше від нуля. Будь-яке від’ємне число менше від нуля. Будь-яке додатне число більше від будь-якого від’ємного. Із двох від’ємних чисел меншим є те, модуль […]...
- ДІЛЬНИКИ і КРАТНІ НАТУРАЛЬНОГО ЧИСЛА. ПРОСТІ ЧИСЛА Розділ 1 ПОДІЛЬНІСТЬ НАТУРАЛЬНИХ ЧИСЕЛ У розділі дізнаєтесь: – що таке дільники і кратні натурального числа; – які є ознаки подільності чисел; – які числа називаються простими та як їх знаходити; – як розкласти число на множники; – що таке найбільший спільний дільник чисел та як його знаходити; – що таке найменше спільне кратне чисел […]...
- Вектор. Модуль і напрям вектора. Рівність векторів УРОК № 42 Тема. Вектор. Модуль і напрям вектора. Рівність векторів Мета уроку: формування понять вектора, модуля вектора, напряму вектора; рівності векторів; формування вмінь застосовувати вивчені означення і властивості до розв’язування задач. Тип уроку: комбінований. Наочність і обладнання: таблиця “Декартові координати та вектори на площині” [13]. Вимоги до рівня підготовки учнів: описують вектор, модуль і […]...
- Взаємно обернені числа Розділ 2 Звичайні дроби §16. Взаємно обернені числа Розглянемо дріб і поміняємо в ньому чисельник і знаменник місцями. Отримаємо дріб Якщо тепер помножити дріб то отримаємо 1: Також отримаємо 1 при множенні 5 на тощо. – Два числа, добуток яких дорівнює 1, називають взаємно оберненими. Легко зробити висновок: щоб знайти дріб взаємно обернений з даним […]...
- Множення Математика – Алгебра Раціональні числа Множення Щоб знайти добуток двох чисел із різними знаками, треба перемножити їхні модулі й поставити перед одержаним числом знак “–”. Щоб перемножити два від’ємних числа, треба перемножити їхні модулі (тобто добуток двох від’ємних чисел є додатне число). При зміні знака одного з множників змінюється знак усього добутку. Якщо добуток містить […]...
- Цілі числа, раціональні числа Урок № 6 5 Тема. Цілі числа, раціональні числа Мета: узагальнити і систематизувати відомості учнів про види чисел; домогтися засвоєння поняття “ціле число”, “раціональне число” і зв’язок між ними; навчити класифікувати числа. Тип уроку: узагальнення і систематизація знань. Хід уроку І. Перевірка домашнього завдання (вибірково у “слабких” перевіряємо зошити) Математичний диктант Варіант 1 [2] 1. […]...
- ЧИТАННЯ І ЗАПИС ЧОТИРИЦИФРОВИХ ЧИСЕЛ. ЗАДАЧІ НА ЗНАХОДЖЕННЯ ЧИСЛА ЗА ЙОГО ЧАСТИНАМИ І ЧАСТИНИ ВІД ЧИСЛА Мета: ознайомити учнів з правилом запису будь-якого чотирицифрового числа; закріплювати вміння читати чотирицифрові числа; повторити правило знаходження частини числа і числа за його частиною; вдосконалювати навички усних і письмових обчислень, розв’язування задач двома способами; розвивати мислення; виховувати інтерес до предмета. ХІД УРОКУ I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ II. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ Завдання 183 – Прочитайте числа, в […]...
- Степінь числа Розділ I НАТУРАЛЬНІ ЧИСЛА І ДІЇ З НИМИ § 3. МНОЖЕННЯ І ДІЛЕННЯ НАТУРАЛЬНИХ ЧИСЕЛ 20. Степінь числа Як ви знаєте, за допомогою добутку зручно записувати суму кількох рівних доданків. Наприклад, 7+7+7 + 7 = 7∙4. У математиці придумали спосіб коротко записувати добуток, у якому всі множники рівні. Наприклад, 7 ∙ 7 ∙ 7 ∙ […]...
- ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА 3. ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА ЧАСТИНАМИ ВИДУ 6 + 2 + 1; 9 ТАБЛИЧНЕ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЕЛ У МЕЖАХ 10 Урок 56. ТАБЛИЦІ ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА 3. ДОДАВАННЯ І ВІДНІМАННЯ ЧИСЛА ЧАСТИНАМИ ВИДУ 6 + 2 + 1; 9 – 2 – 1. ДОДАВАННЯ І ВІДНІМАННЯ ПО 3. РОЗВ’ЯЗУВАННЯ ЗАДАЧ Мета: формувати в учнів уміння складати таблиці додавання і віднімання числа 3; продовжити роботу над складанням […]...
- Степінь натурального числа. Розкладання натурального числа на прості множники Урок № 4 Тема. Степінь натурального числа. Розкладання натурального числа на прості множники Мета: повторити знання учнів про степінь натурального числа з натуральним показником, здобутих у 5 класі, і сформувати вміння використовувати алгоритм розкладання складених чисел на прості множники. Тип уроку: засвоєння нових знань. Хід уроку I. Перевірка домашнього завдання @ Оскільки програмою передбачений дуже […]...
- Додавання двох чисел з різними знаками Розділ 4 Раціональні числа і дії мідними §39. Додавання двох чисел з різними знаками Припустимо, що в понеділок Іван заборгував Сергію 3 грн, а у вівторок повернув борг, тобто віддав Сергію 3 грн. Оскільки борг можна тлумачити як від’ємні числа, а майно – як додатні, то розрахунок між хлопцями можна подати так: -3 + 3 […]...