Неінерційні системи відліку
ФІЗИКА
Частина 1 МЕХАНІКА
Розділ 2 ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ
2.8. Неінерційні системи відліку
Дослід засвідчує, що закони Ньютона справджуються лише в інерційних системах відліку. Будь-яка неінерційна система рухається відносно інерційних систем із деяким прискоренням. У неінерційних системах відліку закони Ньютона не справджуються. Розглянемо це на прикладах.
Нехай на гладенькій платформі без бортів (рис. 2.3) лежить тіло А. Коли платформу зрушити з місця, то тіло зсунеться. Як можна пояснити це явище? З погляду спостерігача,
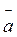0, а тіло А залишилося на попередньому місці.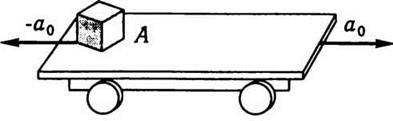
Рис. 2.3.
З погляду спостерігача, який знаходиться в прискореній системі відліку, що зв’язана з платформою, це явище можна пояснити так: тіло А посунулося назад, діставши прискорення. При цьому сила, що діє на тіло, дорівнює нулю, а прискорення – відмінне
Отже, для прискореної системи закон інерції і другий закон динаміки не виконуються. Таку систему називають неінерційною.
Аналогічний приклад можна розглянути з вагоном, який дістає прискорення 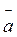1, і м’ячем А, що лежить на гладенькій поличці й почне рухатися з прискоренням 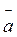1. З погляду пасажира у вагоні (тобто прискореної системи) м’яч набув прискорення, хоч на нього сила не діяла. Отже, тіло в прискореній системі відліку буде в спокої лише під час дії на нього зовнішніх сил.
У механіці часто враховують рух прискореної системи введенням особливих сил, так званих сил інерції. Введення цих сил дає змогу зберегти для тіл, що рухаються відносно неінерційних систем, перший і другий закони динаміки в тій самій формі, яку вони мають для тіл, що рухаються відносно інерційних систем відліку. Це істотно спрощує аналіз руху в кожному окремому випадку.
У першому випадку вважатимемо, що до тіла А прикладено деяку силу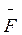 
І. За другим законом Ньютона
Де m – маса тіла; 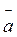0 – прискорення платформи відносно Землі.
У другому випадку сила інерції, що діє на м’яч,
Де m – маса м’яча; 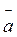1 – прискорення вагона.
Величина 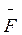І має розмірність сили, проте цього не досить, щоб її вважати силою. Адже різні фізичні величини можуть мати ту саму розмірність (наприклад, робота і момент сили). Сила є механічною дією одного тіла на інше. При цьому завжди має бути відповідна сила “протидії”. Сила – причина “істинного” прискорення, прискорення відносно інерційної системи відліку. Сила інерції прикладена до тіла, але вона не є результатом безпосередньої дії другого тіла, бо такого тіла просто немає. Тому для сили інерції немає і протидії. Вона не проявляється також на “істинному” прискоренні.
Уявімо собі, що на платформі лежить кілька тіл, які відрізняються масами. У формулі (2.15) для різних тіл маса m неоднакова для кожного тіла, а множник а0 – той самий для всіх тіл. Це свідчить про те, що сили інерції, які діють на тіла системи, виникають в результаті прискорення системи відліку (платформи), а не внаслідок взаємодії тіл між собою. Сили інерції збільшуються зі збільшенням прискорення системи відліку і дорівнюють нулю, якщо система відліку рухається рівномірно і прямолінійно.
Отже, за наявністю і значенням сил інерції можна робити висновок про ступінь неінерційності системи. Сили інерції не можна порівнювати з такими силами, як пружні, тертя, тобто силами, що зумовлені дією на тіло інших сил. Сили інерції зумовлені властивостями тієї системи відліку, в якій розглядаються механічні явища.
Вивчення сил інерції не є принципово необхідним. Будь-який рух завжди можна розглянути відносно інерційної системи відліку. Однак практично дуже часто цікавий саме рух відносно неінерційних систем відліку. Використання сил інерції дає можливість розв’язати відповідну задачу безпосередньо у такій системі відліку, що набагато простіше, ніж розглядати рух в інерційній системі.
Отже, введення сил інерції дає змогу описувати рух тіл у будь-яких (як інерційних, так і неінерційних) системах відліку за допомогою одних і тих самих рівнянь руху.
(1 votes, average: 5.00 out of 5)
Loading...