ПЕРЕСТАВНА ВЛАСТИВІСТЬ МНОЖЕННЯ
АРИФМЕТИЧНІ ДІЇ МНОЖЕННЯ ТА ДІЛЕННЯ (продовження)
Урок 123. ПЕРЕСТАВНА ВЛАСТИВІСТЬ МНОЖЕННЯ
Мета: навчати учнів застосовувати переставну властивість множення для знаходження значень виразів; закріпити вміння розв’язувати нерівності способом підбору; вдосконалювати обчислювальні навички; розвивати логічне мислення, увагу; виховувати уважність.
Хід уроку
I. ОРГАНІЗАЦІЙНИЙ МОМЕНТ
II. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ
1. Перевірка домашнього завдання (с. 143, завдання 963; 964)
Завдання 963
– Прочитайте вирази, у відповіді
Завдання 964
– У скільки разів більше хлопчиків грало у волейбол, ніж у теніс?
2. Усна лічба
1) Математична “доріжка”.
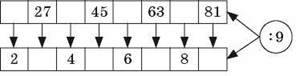
2) Робота в парах.
Гра “Знайди прикладу пару”
Учні по черзі задають приклад на знання табличного множення і ділення. Потрібно скласти відповідний приклад, але з іншим знаком. Наприклад, заданий приклад на множення 9 • 8 = 72,відповідна пара – 72 : 9 = 8 або 72 : 8 = 9.
3. Складання та обчислення значень виразів
– Суму чисел 29 і 34 зменшити в 9 разів.
– Різницю чисел
– Добуток чисел 4 і 7 збільшити на суму чисел 36 і 14.
– Частку чисел 56 і 7 зменшити в 4 рази.
4. Хвилинка каліграфії
– З ряду чисел 12; 15; 18; 21; 24; 27; 28; 30; 32; 36 випишіть ті, які одночасно діляться на 2 і на 3.
Слід звернути увагу учнів, що вийшли числа, які діляться на 6.
III. ПОВІДОМЛЕННЯ ТЕМИ І МЕТИ УРОКУ
– Сьогодні на уроці ми вивчимо переставну властивість множення.
IV. ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ
1. Робота за підручником (с. 143-144)
Завдання 965
Учні виконують обчислення “ланцюжком” усно.
Завдання 966
Учні порівнюють множники і добутки.
– Що змінилося в другому рядку?
Висновок. Множити числа можна в будь-якому порядку. Результат множення від порядку запису множників не змінюється.
– Для чого слід знати переставну властивість множення? (Для зручності і швидкості обчислень.)
Завдання 967. Коментоване розв’язування прикладів
Учні знаходять значення виразів, застосовуючи переставну властивість множення.
Завдання 968
1) Учні відновлюють рівності, застосовуючи переставну властивість множення.
2) Учні розв’язують нерівності способом підбору. Підбирають значення букви к, щоб нерівність k • 7 > 40 була правильною.
Завдання 969
Ознайомившись з умовою задачі, учні складають її короткий запис.
Було – 20 пал.
Витратив – ? тр. по 3 пал.
Залишилося – 11 пал.
Після цього складають план розв’язування.
1) Скільки паличок пішло на складання трикутників?
2) Скільки трикутників склав хлопчик?
Сильніші учні, скориставшись планом, самостійно записують її розв’язання у зошити.
Решта учнів разом з учителем розглядають план розв’язання і визначають дії. Після цього учні складають вираз до задачі.
Завдання 970. Колективне ознайомлення зі змістом задачі, її аналіз Доцільно запропонувати спочатку знайти загальну кількість сторін двох фігур.
Один учень біля дошки розв’язує і пояснює.
Після цього учні знаходять периметри трикутника і шестикутника. Порівнюють їх суму із довжиною дроту.
2. Фізкультхвилинка
V. УЗАГАЛЬНЕННЯ Й СИСТЕМАТИЗАЦІЯ ЗНАНЬ
1. Робота над задачею
Дві бригади лісорубів повинні були заготовити за місяць 90 машин дрів. Перша бригада заготовила 38 машин, а друга – на 5 машин більше. Що дізнаєтеся, виконавши дії:
38 + 5 = [ ]
38 + (38 + 5) = [ ]
90 – 38 – (38 + 5) = [ ]
2.Геометричний матеріал
Периметр прямокутника дорівнює 24 см. Накресліть квадрат з таким самим периметром. Чому дорівнює сторона квадрата?
VI. ПІДБИТТЯ ПІДСУМКІВ. РЕФЛЕКСІЯ
VII. ДОМАШНЄ ЗАВДАННЯ
С. 144, завдання 971; 972.