Перетворення виразів
Уроки № 122, 123
Тема. Перетворення виразів
1. Спростіть вираз і знайдіть його значення при даних значеннях букв:
а) -12b – 7b + 10b – b при b = -0,1; 2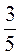 ; -1; -5,7; 0;
; -1; -5,7; 0;
Б) -5а – 8а – 2а – 15a при а = -0,6; 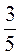 ;
; 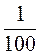 ; 0,002; -1;
; 0,002; -1;
В) -4c + 9с – с + 8 при с = 0; -8; 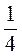 ; -0,25; -2;
; -0,25; -2;
Г) 4(а – b) – 6а + 4b при a = -50; b = 20.
2. Знайдіть значення виразу:
A) -5a + 2b пpи а = –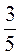 ; b =
; b = 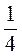 ;
;
Б) -2а – 3b при а = 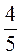 ; b =
; b = 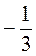
В)  A – 3b при а = 9; b = -1;
A – 3b при а = 9; b = -1;
Г) 3a2 + 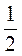 B при a = 3; b =
B при a = 3; b = 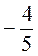 ;
;
Д) 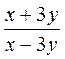 при х = -5; у = -3;
при х = -5; у = -3;
Є) 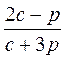 при с =
при с = 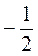 ; р =
; р = 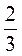 .
.
3. Спростіть вираз і обчисліть його значення:
1) 3х – (2у – 6) – 3у – (2х + 1) при а) x = 0,3, у = -1,2; б) x = -0,3; y = 1,2;
2) -2 – (5a – 3b) – 4 – (-2a + 7b) при а) а = -0,8; b = 0,1; б) а = 0,8; b = -0,1.
4. При натуральних значеннях х формула Ейлера р = х2 – 79х + 1001 дозволяє обчислити 80 простих чисел Використовуючи цю формулу, знайдіть 5 простих чисел.
5. Обчисліть значення
А) а = -1,5; b = -10; с = -0,1;
Б) a = -0,1; b = 0,8; с = -151;
В) а = 6,75; b = 2,5; с = -19,1;
Г) а = 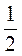 ; b =
; b =  ; с = -0,3
; с = -0,3
6. Обчисліть значення виразу 21|а| – 3|b|, якщо:
А) a = -3,4; b = 2,7;
Б) а = 1,6; b = -0,9.
7. Спростіть вираз:
А) -8,8 + m – n + 28,7 – m;
Б) 9,8 + k – 7,9 + 3,4 – k;
В) -2,3 – 4с,
Г) -0,9b – (-0,6);
Е) -5а – 3,61b,
Ж) -8х – (-0,5у) – 0,6t,
З) 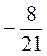 Z – (-t) – 7,24;
Z – (-t) – 7,24;
К) 2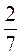 Т –
Т – 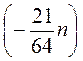 .
.
8. Розкрийте дужки і спростіть вираз:
А) (5,3 + а) – (а + 6,4);
Б) -(9,4 – b) + (-b + 3,7);
В) – (х – 5,8 – y) – (11,3 – х);
Г) -(a – b – 7,4) + (-7,4 + 6а).
9. Зведіть подібні доданки:
А) 7a – 19а + 28a – 2а;
Б) -8х + 16х – 23х + 17x;
В) 2,7m – b + 3,5m – 2,7n;
Г) 2,9t + 1,8 – 5,2t – 1,2;
Є) 2,6p – 0,7k + 1,3 – 3,lp + 2,8k;
Ж) –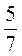 А +
А + 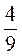 B +
B + 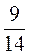 A –
A – 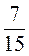 B.
B.
10. Розкрийте дужки і зведіть подібні доданки:
а) 8(6а – 7) – 17а;
11. б) 6b – 7(12 – 3b);
12. в) 1,6(с – 8) + 0,4(8 – 3с);
Г) 1,6(9а – 3b) – (4b – 6а) – 1,5;
Д) -(5,7m – 6,7) – 7,9 – 3,6m;
Є) 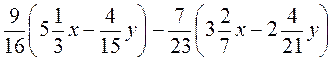 .
.
13. Знайдіть значення виразу:
а) 0,8 |3а – 14| – 0,6(6а – 8) при а = -3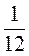 ;
;
Б) 6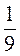 (t – 9) + 2
(t – 9) + 2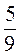 (18 – t) при t = 0,2.
(18 – t) при t = 0,2.
14. Спростіть вираз і знайдіть його значення:
a) (a + b + c) – k + (a – b – c) – k + 3ak при а = 3; b = -5; с = 7; k = -9;
б) (a + b) – с + (b + с) – а + (a – с) b + 2(ab + ас) при а = -1,4; b = -1,5; с = 1,6;
в) (5аb – 3ас + 2) – (аb – 3ас + 1)при а = 3; b = -4; с = -7;
г) -(аb + 4ас – 3bс) – 3(2аb – ас – bс) при а = 1,2; b = -2,4; c = -1,8;
д) (7x – 4y) – z – (5x + 4z) – y + (5y – 3z) – x при x = 3,2; y = -2,5; z = -1,5.
15. Розв’яжіть рівняння:
А) 2х = 15 – x;
Б) 0,3х = 3,9 – х;
В) 7х + 1 = 25 – x;
Г) 5х – 2 = 7х + 11;
Д) 4x – 3 = x + 6;
Е) 4 – 3у = 2у – 1;
Ж) 0,2x + 2,7 = 1,4 – 1,1x;
З) 0,08х + 0,57 = 0,09 – 0,24х;
К) 0,3х + 1,4 = 2,8 – 0,4x;
Л) 13,7 – 2,2х = 1,5x + 2,6;
М) 3(x – 2) = х + 2;
Н) 5 – 2(х – 1) = 4 – x;
О) 0,2(3x – 4) = 1,6(x – 2);
П) (2x + 0,1) – 4(1 – 4x) = 16x – 0,4.
16. Розв’яжіть рівняння:
A) |x + 1| = 2;
Б) |x + 3| = 1;
В) |х – 2| = 3:
Г) |х – 4| = 3;
Д) |5 – х| = 1;
Е) |1 – х| = 4;
Ж) |7 – х| = 3;
З) |8 – х| = 11.