Головна ⇒ 📌Математика ⇒ Перетворення звичайних дробів у десяткові. Нескінченні періодичні десяткові дроби

Перетворення звичайних дробів у десяткові. Нескінченні періодичні десяткові дроби

Розділ 2 Звичайні дроби

§12. Перетворення звичайних дробів у десяткові. Нескінченні періодичні десяткові дроби

Ми вже вміємо перетворювати десяткові дроби у звичайні або у мішані числа, наприклад:

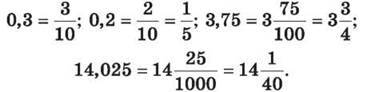
Також ми вміємо перетворювати звичайні дроби із знаменниками 10, 100, 1000, … у десяткові, наприклад,

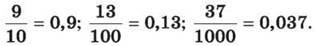
Щоб навчитися перетворювати звичайні дроби з іншими знаменниками у десяткові, необхідно згадати, що звичайний дріб є часткою від ділення чисельника на знаменник. Отже, щоб перетворити

звичайний дріб у десятковий, достатньо чисельник поділити на знаменник.

Наприклад:

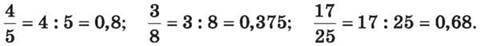
Якщо на десятковий дріб треба перетворити мішане число, достатньо чисельник дробової частини поділити на знаменник і до утвореного десяткового дробу додати цілу частину мішаного числа.

Приклад. Подати число 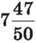десятковим дробом.

Розв’язання.

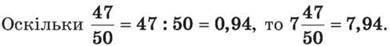
Спробуємо перетворити дріб 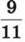на десятковий.

Отже,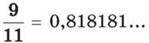

Бачимо, що ділення не закінчилося, тобто

отримали нескінченний десятковий періодичний дріб. А в усіх попередніх випадках ми отримували скінченні десяткові дроби. Цифри 8 і 1, які стоять поряд у запису нескінченного десяткового дробу і повторюються безліч разів поспіль, утворюють період нескінченного десяткового дробу. Це записують так: 0,818181… = 0,(81) (читають: “нуль цілих 81 сота у періоді”). Отже,

Перетворення звичайних дробів у десяткові. Нескінченні періодичні десяткові дроби

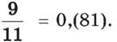
Як бачимо, при перетворенні звичайного дробу на десятковий можуть утворюватися як скінченні, так і нескінченні десяткові дроби. Скінченні дроби утворюються лише тоді, коли в розкладі знаменника на прості множники немає простих множників, крім 2 і 5. В інших випадках утворюється нескінченний періодичний десятковий дріб. Наприклад, дріб 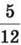перетвориться в періодичний десятковий дріб, бо 12 = 2 ∙ 2 ∙ 3, тобто в розкладі є множник 3. Переконаємося:

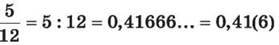(читають: “нуль цілих 41 сота і 6 у періоді”).

Дріб 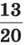перетвориться в скінченний десятковий дріб, бо 20 = 2 ∙ 2 ∙ 5, тобто не містить інших простих множників, крім 2 та 5. Справді,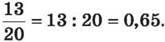

Перетворити звичайні дроби у десяткові можна й іншим способом: домножити чисельник і знаменник на необхідну кількість двійок або п’ятірок так, щоб кількість двійок у знаменнику дорівнювала кількості п’ятірок. Тоді знаменник буде кратним числу 10. Наприклад:

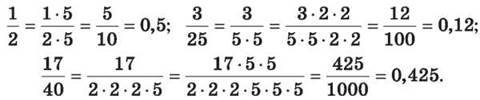
А ще раніше…

У XVII ст. перетворенням звичайного дробу в десятковий займалися італійський математик Бонавентура Кавальєрі (1598- 1647), англійський математик Джон Валліс (1616-1703) та інші.

У процесі нескінченного ділення чисельника звичайного дробу на його знаменник ці вчені отримали періодичні дроби.

У XVIII ст. періодичні дроби також вивчалися німецьким вченим Йоганом Ламбертом (1728-1777) та видатним математиком, фізиком, механіком і астрономом Леонардом Ейлером (1707- 1783). Повну теорію періодичних дробів розробив на початку XIX ст. видатний німецький математик Карл Фрідріх Гаус (1777- 1855).

Термін “період” для групи цифр, що нескінченно повторюються, походить від грецького слова “періодис” – обхід, обертання по колу.

Як перетворити звичайний дріб у десятковий? Чи завжди це перетворення дає скінченний десятковий дріб? Який запис числа називають нескінченним десятковим періодичним дробом? У якому випадку звичайний нескоротний дріб можна перетворити у скінченний десятковий дріб?

274. Прочитай: 0,5; 1,13; 0,(7); 3,1(2); 4,2(37).

275. Перевір, що:

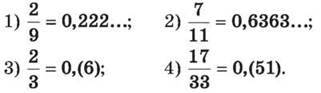
276. Перевір, що:

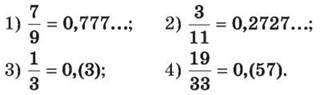
277. Перетвори у десятковий дріб дане число (у випадку отримання нескінченного дробу ділення припини після визначення періоду):

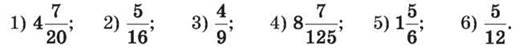
278. Перетвори у десятковий дріб дане число (у випадку отримання нескінченного дробу ділення припини після визначення періоду):

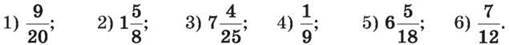
279. Перетвори звичайний дріб у десятковий і обчисли:

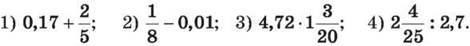
280. Перетвори звичайний дріб у десятковий і обчисли:

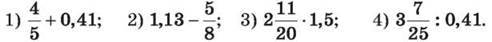
281. Запиши у вигляді нескінченного десяткового періодичного дробу частку:

1) 5 : 99; 2) 19 : 11; 3) 43 : 12; 4) 12,5 : 27.

282. Запиши у вигляді нескінченного десяткового періодичного дробу частку:

1) 10 : 9; 2) 7 : 15; 3) 44 : 6; 4) 25,4 : 11.

283. Порівняй дроби, записавши попередньо звичайні дроби у вигляді десяткових дробів:

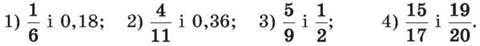
284. Порівняй дроби, записавши попередньо звичайні дроби у вигляді десяткових дробів:

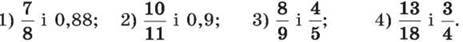
285. Червону стрічку, довжина якої 25 м, розрізали на 7 однакових частин, а зелену стрічку, довжина якої 39 м, розрізали на 11 однакових частин. Довжина якої з отриманих частин більша: червоної чи зеленої?

286. Округли десяткові дроби:

1) до одиниць: 2,73; 3,052; 7,5789;

2) до десятих: 11,82; 0,4859; 11,2342;

3) до сотих: 0,451; 12,499; 1,574.

287. 1) Чи є взаємно простими числа 2012 і 2015? 2) Назви три числа, кожне з яких є взаємно простим з числом 2012 і з числом 2015.

288. Чи можна число 1 подати у вигляді суми дробів 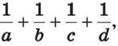де a, b, c, d – непарні натуральні числа?